BZOJ1047: [HAOI2007]理想的正方形

1047: [HAOI2007]理想的正方形

Time Limit: 10 Sec  Memory Limit: 162 MB
Submit: 3530  Solved: 1946
[Submit][Status][Discuss]

Description

有一个a*b的整数组成的矩阵，现请你从中找出一个n*n的正方形区域，使得该区域所有数中

的最大值和最小值的差最小。

Input

第一行为3个整数，分别表示a,b,n的值第二行至第a+1行每行为b个非负整数，表示矩阵中相应

位置上的数。每行相邻两数之间用一空格分隔。

100%的数据2<=a,b<=1000,n<=a,n<=b,n<=1000

Output

　　仅一个整数，为a*b矩阵中所有“n*n正方形区域中的最大整数和最小整数的差值”的最小值。

Sample Input

5 4 2
1 2 5 6
0 17 16 0
16 17 2 1
2 10 2 1
1 2 2 2

Sample Output

1

 

题目大意：求一个子矩阵，使得矩阵最大值减去最小值的差最小。

 

题解：单调队列

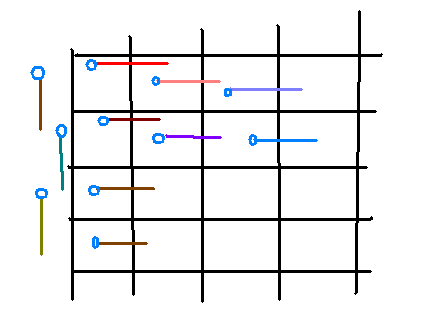
在一个序列上用单调队列会吧？

那么我们在矩阵的每一行用单调队列，求出每行以i为起点，向右n个数的最小最大值

然后我们矩阵的每一个数向右的最小最大值知道了吧？然后我们在每一列上做单调队列，

求我们之前求出的每个数往右的最小最大的值的最小最大值，然后知道每个矩阵的最小

最大值...好绕....

如图，假设现在n=2,我们要找2*2的正方形。蓝色的圆圈表示起点，不同颜色的横线表示以蓝色

的圆圈开头，我们求出了每个横线覆盖范围的最小最大值。然后横向的线段表示求行的最小最大

值。求完之后再对列做单调队列，在所有每行的最小值中当中选出最小的...每行最大的值中选出最

大值。太...太强了..orz...昨天晚上理解了很久的题解...今天晚上终于做完了....

╭︿︿︿╮
{/  o  o /}
(   (oo)  )     =u= mua!...
︶   ︶   ︶

明明只找了20分钟的BUG,我们怎么感觉像一个小时....

 

#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 1007
#define inf 1000000000
using namespace std;

int ans,a,b,n,map[maxn][maxn];
int qmn[maxn],qmx[maxn];
int h_mn,h_mx,t_mn,t_mx;
int hmn[maxn][maxn],hmx[maxn][maxn],ansmn[maxn][maxn],ansmx[maxn][maxn];

int main(){
    scanf("%d%d%d",&a,&b,&n);
    for(int i=1;i<=a;i++)
     for(int j=1;j<=b;j++)
      scanf("%d",&map[i][j]);
    for(int i=1;i<=a;i++){
        h_mn=h_mx=1;
        t_mn=t_mx=0;
        for(int j=1;j<=b;j++){
            while(h_mn<=t_mn&&map[i][qmn[t_mn]]>map[i][j])t_mn--;
            qmn[++t_mn]=j;
            while(h_mx<=t_mx&&map[i][qmx[t_mx]]<map[i][j])t_mx--;
            qmx[++t_mx]=j;
            while(qmn[t_mn]-qmn[h_mn]>=n&&h_mn<=t_mn)h_mn++;
            while(qmx[t_mx]-qmx[h_mx]>=n&&h_mx<=t_mx)h_mx++;
            int t=max(1,j-n+1);
            hmn[i][t]=map[i][qmn[h_mn]];
            hmx[i][t]=map[i][qmx[h_mx]];
        }
    }
    for(int j=1;j<=b;j++){
        h_mn=h_mx=1;t_mn=t_mx=0;
        for(int i=1;i<=a;i++){
            while(h_mn<=t_mn&&hmn[qmn[t_mn]][j]>hmn[i][j])t_mn--;
            qmn[++t_mn]=i;
            while(h_mx<=t_mx&&hmx[qmx[t_mx]][j]<hmx[i][j])t_mx--;
            qmx[++t_mx]=i;
            while(qmn[t_mn]-qmn[h_mn]>=n&&h_mn<=t_mn)h_mn++;
            while(qmx[t_mx]-qmx[h_mx]>=n&&h_mx<=t_mx)h_mx++;
            int t=max(1,i-n+1);
            ansmn[t][j]=hmn[qmn[h_mn]][j];
            ansmx[t][j]=hmx[qmx[h_mx]][j];
        }
    }
    ans=inf;
    for(int i=1;i<=a-n+1;i++)
     for(int j=1;j<=b-n+1;j++)
      ans=min(ans,ansmx[i][j]-ansmn[i][j]);
    cout<<ans<<endl;
    return 0;
}