9.1模拟赛

T1 生日蛋糕

传送门

题目背景

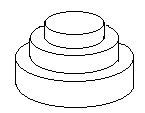
7月17日是Mr.W的生日，ACM-THU为此要制作一个体积为Nπ的M层

生日蛋糕，每层都是一个圆柱体。

设从下往上数第i(1<=i<=M)层蛋糕是半径为Ri, 高度为Hi的圆柱。当i<M时，要求Ri>Ri+1且Hi>Hi+1。

由于要在蛋糕上抹奶油，为尽可能节约经费，我们希望蛋糕外表面（最下一层的下底面除外）的面积Q最小。

令Q= Sπ

请编程对给出的N和M，找出蛋糕的制作方案（适当的Ri和Hi的值），使S最小。

（除Q外，以上所有数据皆为正整数）

题目描述

输入输出格式

输入格式：

 

有两行，第一行为N（N<=20000），表示待制作的蛋糕的体积为Nπ；第二行为M(M<=15)，表示蛋糕的层数为M。

 

输出格式：

 

仅一行，是一个正整数S（若无解则S=0）。

 

输入输出样例

输入样例#1：

100
2

输出样例#1：

68


题解 搜索+剪枝
代码
(1)T了九个点...QAQ

#include<iostream>
#include<cstdio>
#include<cmath>
#define inf 0x7fffffff
using namespace std;

int n,m,ans;

void dfs(int w,int h,int r,int v,int s) {
    if(s>ans)return;
    if(v>n)return;
    if(h<=(m-w)||r<=(m-w))return;
    if(w==m){if(v==n)ans=min(ans,s);return;}
    for(int i=h-1;i>=(m-w);i--)
      for(int j=(m-w);j<=r-1;j++)
       if(w==0)dfs(w+1,i,j,v+j*j*i,s+2*j*i+j*j);
       else 
        dfs(w+1,i,j,v+j*j*i,s+2*j*i);
    return;
} 

int main(){
//    freopen("cake.in","r",stdin);
//    freopen("cake.out","w",stdout);
    scanf("%d",&n);//制作蛋糕的体积。
    scanf("%d",&m);//制作蛋糕的层数。
    int r=sqrt(n)+1;
    ans=inf;
    dfs(0,n,n,0,0);
    if(ans==inf)printf("0\n");
     else  printf("%d\n",ans); 
    return 0;
}

(2)AC代码

可行性剪枝：

建好的体积加上最少的建完的体积仍大于n return 

建好的体积大于n return

最优性剪枝：

当前面积加上建完的最小面积大于当前最优解 return

当前面积大于最优解return

#include<iostream>
#include<cstdio>
using namespace std;
int minv[25],mins[25],ans=1e9;
int n,m;
void dfs(int v,int s,int flr,int lowr,int lowh)//已经建好的体积，面积，还剩下的层数，已经建好的上一层的r和h 
{
    if(flr==0){
        if(s<ans&&v==n)ans=s;
        return;
    }
    if(v+minv[flr]>n||s+mins[flr]>ans||v>n||s>ans)return; 
    if((n-v)/lowr*2+s>ans)return;
    for(int i=lowr-1;i>=flr;i--)
    {
        if(flr==m)s=i*i;
        int mxh=min(lowh-1,(n-v-minv[flr-1])/(i*i));
        for(int j=mxh;j>=flr;j--)
        dfs(v+i*i*j,s+2*i*j,flr-1,i,j);
    }
    return;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        minv[i]=minv[i-1]+i*i*i;//从顶上数i个的最小体积 
        mins[i]=mins[i-1]+i*i*2;//同 最小侧面积 
    }
    dfs(0,0,m,n+1,n+1);
    printf("%d\n",ans);
    return 0;
}

T2 虫食算

传送门

题目描述

所谓虫食算，就是原先的算式中有一部分被虫子啃掉了，需要我们根据剩下的数字来判定被啃掉的字母。来看一个简单的例子：

43#9865#045

+8468#6633

44445509678

其中#号代表被虫子啃掉的数字。根据算式，我们很容易判断：第一行的两个数字分别是5和3，第二行的数字是5。

现在，我们对问题做两个限制：

首先，我们只考虑加法的虫食算。这里的加法是N进制加法，算式中三个数都有N位，允许有前导的0。

其次，虫子把所有的数都啃光了，我们只知道哪些数字是相同的，我们将相同的数字用相同的字母表示，不同的数字用不同的字母表示。如果这个算式是N进制的，我们就取英文字母表午的前N个大写字母来表示这个算式中的0到N-1这N个不同的数字：但是这N个字母并不一定顺序地代表0到N-1)。输入数据保证N个字母分别至少出现一次。

BADC

• CBDA

DCCC 上面的算式是一个4进制的算式。很显然，我们只要让ABCD分别代表0123，便可以让这个式子成立了。你的任务是，对于给定的N进制加法算式，求出N个不同的字母分别代表的数字，使得该加法算式成立。输入数据保证有且仅有一组解

输入输出格式

输入格式：

 

包含四行。第一行有一个正整数N(N<=26)，后面的3行每行有一个由大写字母组成的字符串，分别代表两个加数以及和。这3个字符串左右两端都没有空格，从高位到低位，并且恰好有N位。

 

输出格式：

 

包含一行。在这一行中，应当包含唯一的那组解。解是这样表示的：输出N个数字，分别表示A，B，C……所代表的数字，相邻的两个数字用一个空格隔开，不能有多余的空格。

 

输入输出样例

输入样例#1：

5
ABCED
BDACE
EBBAA

输出样例#1：

1 0 3 4 2

说明

对于30％的数据，保证有N<＝10；

对于50％的数据，保证有N<＝15；

对于全部的数据，保证有N<＝26。

noip2004提高组第4题

题解

暴搜

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm> 
using namespace std;

int use[29],k[29],q[29][5],las[29];
int n;char x;

inline void print(){
    for(int i=1;i<=n;i++)printf("%d ",k[i]);
    exit(0);
}

inline int check1(int px){
    for(int i=n;i>=px+1;i--){
        if(k[q[px][1]]!=-1&&k[q[px][2]]!=-1&&k[q[px][3]]!=-1){
        //    if((k[q[px][1]]+k[q[px][2]]+las[px-1])%n!=k[q[px][3]])
        if((k[q[px][1]]+k[q[px][2]])%n!=k[q[px][3]]&&(k[q[px][1]]+k[q[px][2]]+1)%n!=k[q[px][3]])
            return false;
        }
    }
    return true;
}

int check2(int px){
    if(k[q[px][1]]!=-1&&k[q[px][2]]!=-1&&k[q[px][3]]!=-1){
        if((k[q[px][1]]+k[q[px][2]]+las[px-1])%n!=k[q[px][3]]){
            return false;
        }else las[px]=(k[q[px][1]]+k[q[px][2]]+las[px-1])/n;
    }
    if(k[q[px][1]]!=-1&&k[q[px][2]]!=-1&&k[q[px][3]]==-1){
        int z=(k[q[px][1]]+k[q[px][2]]+las[px-1])%n;
        if(use[z])return false;
    }
    if(k[q[px][1]]==-1&&k[q[px][3]]!=-1&&k[q[px][2]]!=-1){
        int z=(k[q[px][3]]-k[q[px][2]]-las[px-1]+n)%n;
        if(use[z])return false;
    }
    if(k[q[px][2]]==-1&&k[q[px][1]]!=-1&&k[q[px][2]]!=-1){
        int z=(k[q[px][3]]-k[q[px][1]]-las[px-1]+n)%n;
        if(use[z])return false;
    }
    return true;
}

void dfs(int posx,int posy){
    if(k[q[posx][posy]]==-1){
        if(posy==1||posy==2)
        for(register int i=n-1;i>=0;i--){
            if(use[i]==0){
                use[i]=1;k[q[posx][posy]]=i;
                if(check1(posx)&&check2(posx))dfs(posx,posy+1);
                use[i]=0;k[q[posx][posy]]=-1;
            }
        }else{
            int z=k[q[posx][1]]+k[q[posx][2]]+las[posx-1];
            if(z>=n)z%=n;
            if(use[z]==0){
                use[z]=1;k[q[posx][posy]]=z;
                if(posx==n)print();
                if(check1(posx)&&check2(posx))
                dfs(posx+1,1);
                use[z]=0;k[q[posx][posy]]=-1;
            }
        }
    }else{
        if(check1(posx)&&check2(posx)){
            if(posx==n&&posy==3)print();
            if(posy==1||posy==2)dfs(posx,posy+1);
            else dfs(posx+1,1);
        }
    }
}

int main(){
    scanf("%d",&n);scanf("\n");
    register int i;
    for(i=1;i<=n;i++){scanf("%c",&x);q[i][1]=x-'A'+1;}
    scanf("\n");
    for( i=1;i<=n;i++){scanf("%c",&x);q[i][2]=x-'A'+1;}
    scanf("\n");
    for(i=1;i<=n;i++){scanf("%c",&x);q[i][3]=x-'A'+1;}
    for(i=1;i<=n/2;i++)
    {swap(q[i][1],q[n-i+1][1]);swap(q[i][2],q[n-i+1][2]);swap(q[i][3],q[n-i+1][3]);}
    memset(k,-1,sizeof(k));
    dfs(1,1);
    return 0;
}