【学习笔记】一维差分/二维差分

一、一维差分

1、引入

一个序列 5 4 6 2 7

每个数减去前面一个数得到一个新的序列，第一个数默认减0，得到新序列5  -1  2  -4  5

这个新序列就是差分数组

将差分数组求前缀和 ，得到原序列 5 4 6 2 7

2、区间操作

假设要在区间[2,4]内每个数加2。

接下来对差分数组5 -1 2 -4 5进行如下操作。

第一行为数组下标。在下标为2处+2，在下标为5处-2。

 

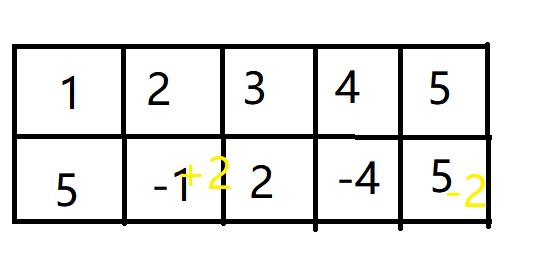
得到新的差分数组 5 1 2 -4 3。

对新的差分数组求前缀和，得到数组5 6 8 4 7。发现实现了区间[2,4]每个数+2的操作。

 

二、二维差分

1、引入

定义：设初始数组为a[][],差分数组为p[][]。

·二维前缀和定义：对于一个左上角为[1,1],右下角为[n,m]的矩阵。二维前缀和数组s[i][j]表示左上角为[1,1]，右下角为[i,j]的矩阵的所有数的和。

可知数组a[][]的前缀和矩阵s[][]   s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]。

·二维差分数组：p[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]。

类比一维差分：对二维数组求得二维差分数组，对二维差分数组求前缀和得到原二维数组。

一个例子：

a[][]: 

1 2 4 3 

5 1 2 4

6 3 5 9

它对应的差分矩阵p[][]:

1   1    2    -1
4   -5   -1   3
1   1    1    2

差分矩阵p[][]的前缀和矩阵：

1 2 4 3

5 1 2 4

6 3 5 9

就是原矩阵a[][]。  

2、区间操作

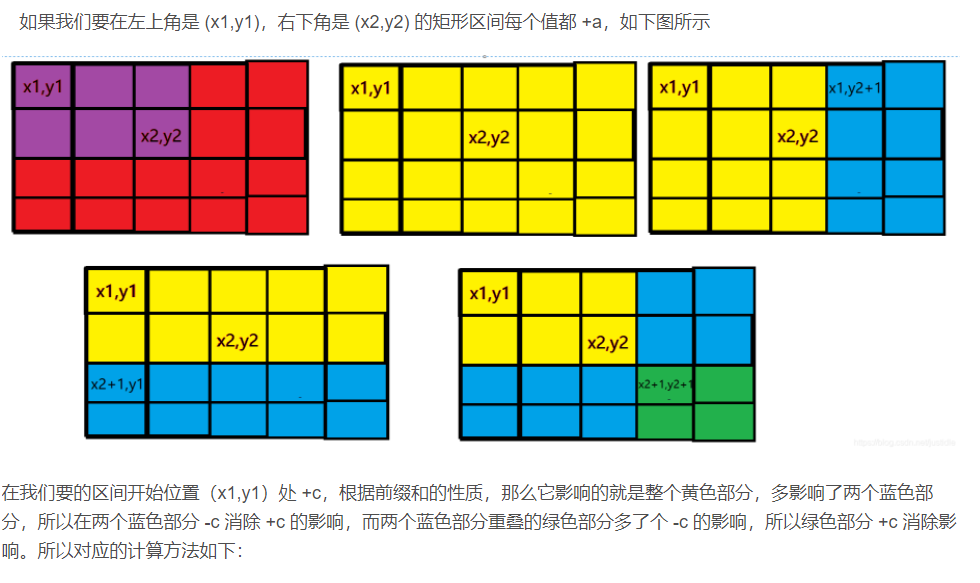
假设要对左上角为[x1,y1],右下角为[x2,y2]的矩阵的每个数加c；

接下来要对差分矩阵p[][]进行如下操作。

p[x1][y1]+=c；

p[x1][y2+1]-=c;

p[x2+1][y1]-=c;

p[x2+1][y2+1]+=c;

原因如下：下图来自https://blog.csdn.net/justidle/article/details/104506724

 

3、题目

（1）传送门

#include<bits/stdc++.h>
using namespace std;
#define N 1009
int n,m,q;

int a[N][N];
int p[N][N];
int s[N][N];

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            cin>>a[i][j];
            p[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];
        } 
    }
    for(int i=1;i<=q;i++)
    {
        int x1,y1,x2,y2,c;
        cin>>x1>>y1>>x2>>y2>>c;
        p[x1][y1]+=c;
        p[x1][y2+1]-=c;
        p[x2+1][y1]-=c;
        p[x2+1][y2+1]+=c;    
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            s[i][j]=s[i][j]+s[i-1][j]+s[i][j-1]-s[i-1][j-1]+p[i][j];
            cout<<s[i][j]<<" ";
        }    
        cout<<endl;
    }
    return 0;
}

（2）2020小米邀请赛J-Matrix Subtraction

题目大意为：给出nXm矩阵，能否每次选中aXb的子矩阵，将子矩阵中的每个数-1，使nXm矩阵减为0.

#include<bits/stdc++.h>
using namespace std;
#define N 1003

int T;
int n,m,a,b;
int c[N][N],p[N][N];
int s[N][N];

int slove(int x1,int y1,int x2,int y2,int c)
{
    p[x1][y1]+=c;
    p[x1][y2+1]-=c;
    p[x2+1][y1]-=c;
    p[x2+1][y2+1]+=c; 
}


int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cin>>T;
    while(T--)
    {
        cin>>n>>m>>a>>b;
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                cin>>c[i][j];
                p[i][j]=c[i][j]-c[i-1][j]-c[i][j-1]+c[i-1][j-1];
            }
        }
        bool flag=true;
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                p[i][j]=p[i][j]+p[i-1][j]+p[i][j-1]-p[i-1][j-1];
                if(p[i][j]<0) {flag=false; break;}
                if(p[i][j]==0){continue;}
                if(p[i][j]>0)
                {
                    if(i+a-1>n||j+b-1>m) {flag=false;break;}
                    slove(i,j,i+a-1,j+b-1,-p[i][j]);
                }
                
            }
            if(!flag) break;
        }
        if(flag) cout<<"^_^\n";
        else cout<<"QAQ\n";
    }
    return 0;
}