Backtracking_51. N皇后

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

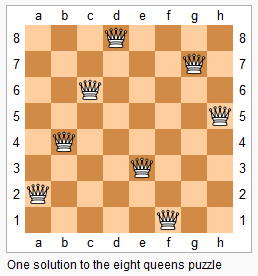
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例:

输入: 4
输出: [
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],

["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

提示：

皇后，是国际象棋中的棋子，意味着国王的妻子。皇后只做一件事，那就是“吃子”。当她遇见可以吃的棋子时，就迅速冲上去吃掉棋子。当然，她横、竖、斜都可走一到七步，可进可退。（引用自 百度百科 - 皇后 ）

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/n-queens

---

思路：

用一个数组来记录路经，即set记录路径，set【0】 = 1表示在第一行，皇后要下在第二个位置you know me

然后用递归回溯的方法，先把set路径都找到，即0~n的set值都填满

然后去调整格式就行了

class Solution {
    //棋盘大小是N*N，定义一个二维数组来表示棋盘
    String [][] chessBoard;
    //定义一个一维数组来存储皇后的位置
    int [] set;
    public List<List<String>> solveNQueens(int n) {
        chessBoard = new String[n][n];
        set = new int[chessBoard.length];
        List<List<String>> res = new LinkedList<>();  //用于接收答案
        List<String> path = new ArrayList<>();  // 用于保存当前路径
        if(n == 1){
            path.add("Q");
            res.add(new ArrayList<>(path));
            return res;
        }
        dfs(chessBoard,0,set,path,res);
        return res;
    }

    //这是一个找皇后位置并落子的函数
    public void dfs(String [][] chessBoard,int n,int [] set,List<String> path,List<List<String>> res){
        if (n == chessBoard.length){
            for (int i = 0; i < n; i++) {
                String temp = "";
                for (int j = 0; j < n; j++) {
                    if (j == set[i]){
                        chessBoard[i][j] = "Q";
                    }else {
                        chessBoard[i][j] = ".";
                    }
                    temp += chessBoard[i][j];
                }
                path.add(temp);
                if (path.toArray().length == n){
                    res.add(new ArrayList<>(path));
                    path.clear();
                }
            }
            return;
        }
        for (int i = 0; i < chessBoard.length; i++) {
            set[n] = i;
            if (judge(chessBoard,n)){
                dfs(chessBoard,n + 1,set,path,res);
            }
        }
    }

    //这是一个判断的函数,假设放置第n个皇后
    public boolean judge(String [][] chessBoard,int n){
        int len = chessBoard.length;
        for (int i = 0; i < n; i++) {
            if (set[i] == set[n] || (Math.abs(n - i) == Math.abs(set[n] - set[i]))){
                return false;
            }
        }
        return true;
    }
}