自引导滤波的定点化计算与近似处理

目的：用于HDR和超夜算法中的单帧降噪，提高计算效率。

原引导滤波公式参照：https://blog.csdn.net/Katiness/article/details/79507729

这里的自引导的意思是输入图像p同时作为引导图I。

*****改进计算公式，系数求解变为a_k = σ²/(σ²+ε)；

*****输出图q = a_k*p + (1-a_k)*μ，μ为均值。

 自身作为引导图最终a_k计算公式简化为：

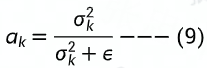
 输出图计算公式简化为：

 

 

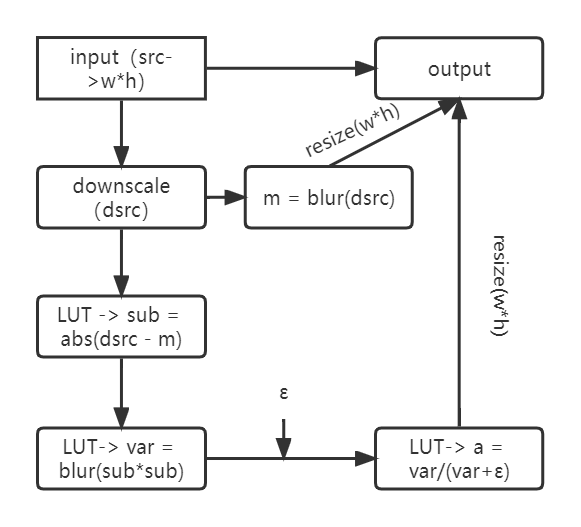
计算方差σ²时，可以有两种方式：

1. 利用σ²=1/n∑(p_i-μ)²，求出原图与均值图的差值再计算平方即可得到方差；

1.1 原图src下采样dsrc，计算均值滤波图mean = blur(dsrc)（选择一定的滤波尺寸，均为uchar类型）；

1.2 查表或者absdiff计算差值绝对值sub = abs(dsrc - mean)；

1.3 sub平方再做均值滤波得方差var = blur(sub*sub)，ushort存储，最大值为65535（注意此步运算是做了近似的，因为这种

方式计算方差，对窗口的每个像素点减去的应该是同一个该窗口内所有像素的均值，实际上是减去了不同均值，每个位置减掉一个

不同均值，这里姑且认为这些均值差异较小，代替了窗口的同一均值；这样可能会使保边效果变差，可能会有斑块感，因为方差或大或小了）；

1.4 设定正则系数ε（决定滤波强度），根据ε值建表（最大长度255*255+1），需要定点化，右移8位，最大255；

通过var的值查表计算的a_k；

1.5 a_k可以滤波也可以不滤，效果影响并不大；

1.6 将a_k和mean都resize到原图尺寸，进行融合计算，此时：

dst[i] = (a[i]*src[i] + (255^a[i])*mean[i] + 256 or 128)>>8

 注意*****：为了提高最终图的清晰度，因为这里系数已经计算完成，所以可以在最终融合计算截断使用高斯滤波图代替均值图；

同时可以考虑在计算系数时对原图做一次高斯滤波消除噪声点的干扰，使最终图噪声形态更佳。

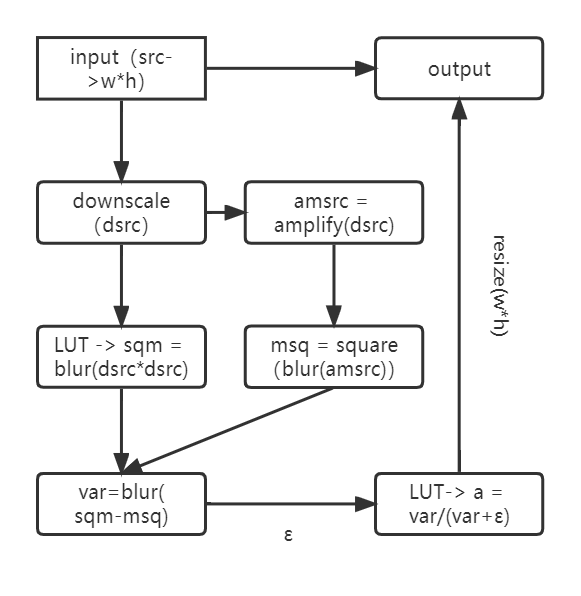
2. 利用σ²=1/n∑(p_i)² - μ²，求出原图平方求平均，再求均值图的平方，两者做差也可以得到方差；

计算方差与方法一差别是利用σ² = mean(p²) - (mean(p))²;

求输入图dsrc的平方再均值滤波，sqm = blur(dsrc*dsrc)；

计算dsrc的均值滤波再平方，mean = blur(dsrc)，msq = mean*mean;

方差var = sqm - msq；

这样计算会存在精度损失，即求均方项msq时，因为mean已经丢掉了精度，再做平方精度丢失被放大，如100.1的平方与100的平方相差约20；

所以计算均值滤波过程中，需要先将dsrc放大倍率（ushort或int存储）以提高均值滤波后保留的精度；

计算sqm时使用查表，同时减少数据类型学转换（uchar到ushort）；

计算var时使用循环并移位运算，var使用ushort存储；

其它步骤与方法一相同。

这个计算过程与opencv引导滤波是基本一致的，但是效果上要想与其一直，需要对a_k做均值滤波，同时(1-a_k)*mean的结果也需要均值滤波才能解决边缘过渡的

问题。

注意*****：在放大倍率计算过程中，对原图做一次小尺寸高斯滤波，减少噪声点的干扰，使得最终图的噪声形态更均匀。

滤波保护

灰度保护：在一些特定的场景，需要对高光或暗光处做滤波保护，即不做滤波处理，在最后计算输出图q = a_k*p + (1-a_k)*μ过程中可以增加阈值判断，高于阈值或低于阈值，全部为输入图像素值。

系数值保护：还可以对计算得到的a_k值截断，高于阈值保留，低于阈值全部设置为0或者使用同一个小值替换。

黑点（斑）抑制

超夜应用中，由于信号很弱，sensor成像质量很差，会存在很多异常的黑点（非零值，且经过MFNR后值也会被拉起来），通过设定灰度阈值和系数阈值，

认为在暗部区域，系数值理论上不应该太大，如果出现大的系数就可能是黑点或黑斑，就将该系数做一个衰减，这里可能会出现误判，所以系数值阈值不能设置过小。实际测试中使用灰度阈值45，系数阈值100，效果上对黑点（黑斑）有较好的抑制作用。这样处理误判会是部分暗部细节会有些损失，可以通过回加方式恢复一些。

算法流程图

以差值平方计算方差近似计算算法流程图：

 

 

以方均减均方（中间包括放大倍数以保持更高的均值滤波精度）近似计算算法流程图：