最小生成树
最小生成树:
最小生成树(Minimum Spanning Tree,MST)是在一个给定的无向图G(V,E)中求一棵树T,使得这棵树拥有图G中的所有顶点,且所有边都是来自图G中的边,并且满足整棵树的边权之和最小。
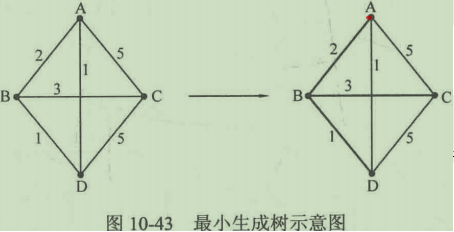
图10-43给出了一个图G及其最小生成树T,其中较粗的线即为最小生成树的边。可以看到,边AB、BC、BD包含了图G的所有顶点,且由它们生成的树的边权之和为6,是所有生成树中权值最小的(例如边AD、BD、CD生成的树,其边权之和为7,大于之前给出的树的边权之和)。
最小生成树有3个性质需要掌握:
①最小生成树是树,因此其边数等于顶点数减1,且树内一定不会有环。
②对给定的图G(V,E),其最小生成树可以不唯一,但其边权之和一定是唯一的。
③由于最小生成树是在无向图上生成的,因此其根结点可以是这棵树上的任意一个结点。于是,如果题目中涉及最小生成树本身的输出,为了让最小生成树唯一,一般都会直接给出根结点,读者只需以给出的结点作为根结点来求解最小生成树即可。
求解最小生成树一般有两种算法,即prim算法与kruskal算法。
这两个算法都是采用了贪心法的思想,只是贪心的策略不太一样。
Prim算法与Kurskal算法比较
(1)从算法的思想可以看出,如果图G中的边数较小时,可以采用Kruskal算法,因为Kruskal 算法每次查找最短的边;边数较多可以用Prim算法,因为它是每次加一个结点。
可见,Kruskal算法适用于稀疏图,而Prim算法适用于稠密图。
(2)从时间上讲,Prim算法的时间复杂度为O(n2),Kruskal 算法的时间复杂度为O(eloge)。
(3)从空间上讲,显然在Prim算法中,只需要很小的空间就可以完成算法,因为每一次都是从V-U集合出发进行扫描的,只扫描与当前结点集到U集合的最小边。但在Kruskal算法中,需要对所有的边进行排序,对于大型图而言,Kruskal算法需要占用比Prim算法大得多的空间。


