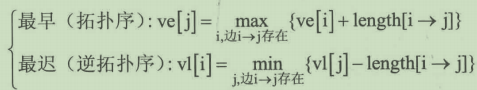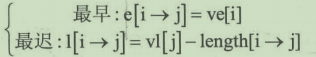关键路径详解

AOV网：

顶点活动（Activity On Vertex，AOV）网是指用顶点表示活动，而用边集表示活动间优先关系的有向图。例如图10-57的先导课程示意图就是AOV网，其中图的顶点表示各项课程，也就是“活动”；有向边表示课程的先导关系，也就是“活动间的优先关系”。显然，图中不应当存在有向环，否则会让优先关系出现逻辑错误。

​

AOE网： 

边活动（Activity On Edge，AOE）网是指用带权的边集表示活动，而用顶点表示事件的有向图，其中边权表示完成活动需要的时间。例如图10-59中，边a1~a6表示需要学习的课程，也就是“活动”，边权表示课程学习需要消耗的时间；顶点V1~V6。表示到此刻为止前面的课程已经学完，后面的课程可以开始学习，也就是“事件”（如V5表示a4计算方法和a3实变函数已经学完，a6泛函分析可以开始学习。从另一个角度来看，a6只有当a4和a5都完成时才能开始进行，因此当a4计算方法学习完毕后必须等待a5实变函数学习完成后才能进入到a6泛函分析的学习），显然“事件”仅代表一个中介状态。

​

源点：在AOE网中，没有入边的顶点称为源点；如顶点V1 

终点：在AOE网中，没有出边的顶点称为终点；如顶点V6 

AOE网的性质：

·只有在进入某顶点的活动都已经结束，该顶点所代表的事件才发生；

·只有在某顶点所代表的事件发生后，从该顶点出发的各活动才开始；

AOE网中的最长路径被称为关键路径（强调：关键路径就是AOE网的最长路径），而把关键路径上的活动称为关键活动，显然关键活动会影响整个工程的进度。

关键概念：

​

1.事件的最早发生时间ve[k]（earliest time of vertex）：即顶点vk的最早发生时间。

从源点向终点方向计算

ve[0] = 0

ve[1] = ve[0] + a0 = 0 + 4 = 4

ve[2] = max( ve[0] + a1, ve[1] + a2 ) = max(0 + 3, 4 + 2 = 6

ve[3] = max(ve[1] + a4, ve[2] + a3) = max(4 + 6, 3 + 4) = 10

 

2.事件的最晚发生时间vl[k]（latest time of vertex）：即顶点vk的最晚发生时间，也就是每个顶点对应的事件最晚需要开始的时间，超出此时间将会延误整个工期。

从终点向源点方向计算

vl[3] = ve[3] = 10

vl[2] = vl[3] - a3 = 10 - 4 = 6

vl[1] = min(vl[3] - a4, vl[2] - a2) = min(10-6, 6-2) = 4//之所以求最小，保证其他的点的最晚发生时间

vl[0] = min(vl[2] - a1, vl[1] - a0) = min(4-4, 4-2) = 0 

 

3.活动的最早开工时间e[k]（earliest time of edge）：即弧ax的最早发生时间。

5条边，5个活动

e[0] = ve[0] = 0

e[1] = ve[0] = 0

e[2] = ve[1] = 4

e[3] = ve[2] = 6

e[4] = ve[1] = 4

 

4.活动的最晚开工时间l[k]（latest time of edge）：即弧ak的最晚发生时间，也就是不推迟工期的最晚开工时间。

e[0] = v[1] - a0 = 4 - 4 = 0

e[1] = vl[2] - a1 = 6 - 3 = 3

e[2] = vl[2] - a2 = 6 - 2 = 4

e[3] = vl[3] - a3 = 10 - 4 = 6

e[4] = vl[3] - a4 = 10 - 6 = 4 

活动的最早开始时间和最晚开始时间相等，则说明该活动时属于关键路径上的活动，即关键活动

算法设计：

关键路径算法是一种典型的动态规划法，设图G=(V, E)是个AOE网，结点编号为1,2,...,n，其中结点1与n 分别为始点和终点，ak=<i, j>∈E是G的一个活动。算法关键是确定活动的最早发生时间ve[k]和最晚发生时间vl[k]，进而获取顶点的最早开始时间e[k]和最晚开始时间l[k]。

根据前面给出的定义，可推出活动的最早及最晚发生时间的计算方法：

e(k) = ve(i)

l(k) = vl(j) - len(i,j)

​

结点的最早发生时间的计算，需按拓扑次序递推：

ve(1) = 0

ve(j) = MAX{ etv(i)+len(i, j) }

 

对所有<i,j> ∈E的i  结点的最晚发生时间的计算，需按逆拓扑次序递推：

vl(n) = ve(n)

vl(i) = MIN{vl(j) - len(i, j)} 对所有<i,j>∈E的j

 

这种计算方法， 依赖于拓扑排序， 即计算ve( j) 前，应已求得j 的各前趋结点的ve值，而计算vl(i)前，应已求得i的各后继结点的vl值。ve的计算可在拓扑排序过程中进行，即在每输出一个结点i后，在删除i的每个出边<i,j>（即入度减1）的同时，执行

if ( ve[i]+len(i,j)) > ve[j] )

ve[j] = ve[i] + len(i,j)

 

这时会发现，如果想要获得ve[j]的正确值，ve[il]~ve[ik]必须已经得到。有什么办法能够在访问某个结点时保证它的前驱结点都已经访问完毕呢？没错，使用拓扑排序就可以办到。

当按照拓扑序列计算ve数组时，总是能保证计算ve[i]的时候ve[il]~ve[ik]都已经得到。但是这时又碰到另一个问题，通过前驱结点去寻找所有后继结点很容易，但是通过后继结点V；去寻找它的前驱结点V1~Vx似乎没有那么直观。一个比较好的办法是，在拓扑排序访问到某个结点时，不是让它去找前驱结点来更新ve[i]，而是使用ve[i]去更新其所有后继结点的ve值。通过这个方法，可以让拓扑排序访问到V；的时候，V1~Vk一定都已经用来更新过ve[i]，此时的ve[i]便是正确值，就可以用它去更新V；的所有后继结点的ve值。

 1 //拓扑序列
 2 
 3 stack<int>topOrder;
 4 
 5 //拓扑排序，顺便求ve数组
 6 
 7 bool topologicalSort()
 8 
 9 {
10 
11     queue<int>q;
12 
13     for(int i=0;i<n;i++)
14 
15         if(inDegree[i]==0)
16 
17             q.push(i);
18 
19     while(!q.empty())
20 
21     {
22 
23         int u=q.front();
24 
25         q.pop();
26 
27         topOrder.push(u);//将u加入拓扑序列
28 
29         for(int i=0;i<G[u].size();i++)
30 
31         {
32 
33             int v=G[u][i].v;//u的i号后继结点编号为v
34 
35             inDegree[v]--;
36 
37             if(inpegree[v]==0)
38 
39                 q.push(v);
40 
41             //用ve[u]来更新u的所有后继结点
42 
43             if(ve[u]+G[u][i].w> ve[v])
44 
45                 ve[v]=ve[u]+G[u][i].w;
46 
47         }
48 
49     }
50 
51     if(toporder.size()== n)
52 
53         return true;
54 
55     else
56 
57         return false;
58 
59 }

同理，如图10-64所示，从事件V出发通过相应的活动ar1~ark可以到达k个事件V1~Vk，活动的边权为length[r1]~length[rk]。假设已经算好了事件V1~Vk的最迟发生时间xl[j1]～vl[jk]，那么事件Vi的最迟发生时间就是vl[j1]-length[r1]~vl[jk]-length[rk]中的最小值。此处取最小值是因为必须保证Vj1~Vjk的最迟发生时间能被满足；可以通过下面这个公式辅助理解。

 和ve数组类似，如果需要算出vl[i]的正确值，vl[j1]~vl[jk]必须已经得到。这个要求与ve数组的刚好相反，也就是需要在访问某个结点时保证它的后继结点都已经访问完毕，而这可以通过使用逆拓扑序列来实现。幸运的是，不必再做一次逆拓扑排序来得到逆拓扑序列，而是可以通过颠倒拓扑序列来得到一组合法的逆拓扑序列。此时会发现，在上面实现拓扑排序的过程中使用了栈来存储拓扑序列，那么只需要按顺序出栈就是逆拓扑序列。而当访问逆拓扑序列中的每个事件Vi时，就可以遍历Vi的所有后继结点Vj1~Vjk，使用vI[j1]~vl[jk]来求出vl[i]。

这部分的代码如下所示：

 1 fill(vl，v1+n，ve[n-1]);//v1数组初始化，初始值为终点的ve值
 2 
 3 //直接使用toporder出栈即为逆拓扑序列，求解v1数组
 4 
 5 while(！topOrder.empty())
 6 
 7 {
 8 
 9     int u=topOrder.top();//栈顶元素为u
10 
11     topOrder.pop();
12 
13     for(int i=0;i<G[u].size();i++)
14 
15     {
16 
17         int v=G[u][i].v;//u的后继结点v
18 
19         //用u的所有后继结点v的v1值来更新v1[u]
20 
21         if(vl[v]-G[u][i].w < vl[u])
22 
23             vl[u]=vl[v]-G[u][i].w;
24 
25     }
26 
27 }

        通过上面的步骤已经把求解关键活动的过程倒着推导了一遍，下面给出上面过程的步骤总结，即“先求点，再夹边”：

①按拓扑序和逆拓扑序分别计算各顶点（事件）的最早发生时间和最迟发生时间：

​

②用上面的结果计算各边（活动）的最早开始时间和最迟开始时间：

​

③e[i-→] = l[i-→i]的活动即为关键活动。

主体部分代码如下（适用汇点确定且唯一的情况，以n-1号顶点为汇点为例）：【主体代码】

求取关键路径：

 1 //遍历邻接表的所有边，计算活动的最早开始时间e和最迟开始时间1
 2 
 3 for(int u=0；u<n；u++)
 4 
 5 {
 6 
 7     for(int i=0；i<G[u].size()；i++)
 8 
 9     {
10 
11         int v=G[u][i].v，w=G[u][i].w；
12 
13         //活动的最早开始时间e和最迟开始时间1
14 
15         int e=ve[u]，l=vl[v]-w；
16 
17         //如果e==1，说明活动u->v是关键活动
18 
19         if(e==1)
20 
21         printf("%d->%d\n"，u,v)；//输出关键活动}
22 
23     }
24 
25     return ve[n-1]；//返回关键路径长度
26 
27 }

 

在上述代码中，没有将活动的最早开始时间e和最迟开始时间l存储下来，这是因为一般来说e和l只是用来判断当前活动是否是关键活动，没有必要单独存下来。如果确实想要将它存储下来，只需要在结构体Node中添加域e和1即可。

如果事先不知道汇点编号，有没有办法比较快地获得关键路径长度呢？当然是有办法的，那就是取ve数组的最大值。原因在于，ve数组的含义是事件的最早开始时间，因此所有事件中ve最大的一定是最后一个（或多个）事件，也就是汇点。于是只需要在fill函数之前添加一小段语句，然后改变下vl函数初始值即可，代码如下：

 1 int maxLength = 0;
 2 
 3 for(int i=0; i<n; ++i)
 4 
 5 {
 6 
 7     if(ve[i] > maxLength)
 8 
 9         maxLength = ve[i];
10 
11 }
12 
13 fill(vl, vl + n, maxLength);

 

posted @ 2019-11-22 15:49  自由之翼Az  阅读(1564)  评论(0)  编辑  收藏  举报