PAT甲级——A1146 TopologicalOrder【25】
This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.
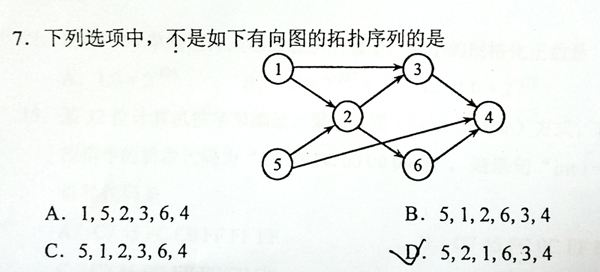
Input Specification:
Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 1,000), the number of vertices in the graph, and M (≤ 10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.
Output Specification:
Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.
Sample Input:
6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6
Sample Output:
3 4
Solution:
使用邻接矩阵来保存这个有向矩阵,并且把每个节点的入度计算,遍历判断的序列,每经过一个节点就判断该节点入度是不是为0,若不是,说明不是拓扑序列
每经过一个节点,将其指向节点的入度-1,表明指向节点的父节点遍历完毕,从而保证了整个序列是个拓扑序列
1 #include <iostream> 2 #include <vector> 3 #include <queue> 4 #include <algorithm> 5 using namespace std; 6 7 8 int main() 9 { 10 int n, m, k; 11 cin >> n >> m; 12 vector<vector<int>>v(n + 1); 13 vector<int>in(n + 1, 0), temp, res;//节点的入度 14 for (int i = 0; i < m; ++i) 15 { 16 int a, b; 17 cin >> a >> b; 18 v[a].push_back(b); 19 in[b]++; 20 } 21 cin >> k; 22 for (int i = 0; i < k; ++i) 23 { 24 bool flag = true; 25 temp = in; 26 for (int j = 0; j < n; ++j) 27 { 28 int x; 29 cin >> x; 30 if (temp[x] != 0)flag = false; 31 for (auto a : v[x])--temp[a];//出现一次入度减一 32 } 33 if (!flag) 34 res.push_back(i); 35 } 36 for (int i = 0; i < res.size(); ++i) 37 cout << (i == 0 ? "" : " ") << res[i]; 38 return 0; 39 }



