PAT甲级——A1099 Build A Binary Search Tree

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
• Both the left and right subtrees must also be binary search trees.

Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.

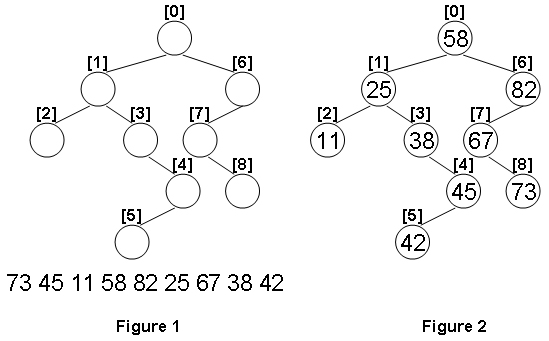
Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤) which is the total number of nodes in the tree. The next N lines each contains the left and the right children of a node in the format left_index right_index, provided that the nodes are numbered from 0 to N−1, and 0 is always the root. If one child is missing, then − will represent the NULL child pointer. Finally N distinct integer keys are given in the last line.

Output Specification:

For each test case, print in one line the level order traversal sequence of that tree. All the numbers must be separated by a space, with no extra space at the end of the line.

Sample Input:

9
1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1
73 45 11 58 82 25 67 38 42

Sample Output:

58 25 82 11 38 67 45 73 42

#include <iostream>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
struct Node
{
    int val, l, r;
}node[105];
vector<int>nums(105), levelOrder;
int N, k = 0;
void inOrderTravel(int root)//得到树的中序遍历
{
    if (root == -1)
        return;
    inOrderTravel(node[root].l);
    node[root].val = nums[k++];
    inOrderTravel(node[root].r);
}
void levelOrderTravel(int root)//得到树的中序遍历
{
    queue<int>q;
    q.push(root);
    while (!q.empty())
    {
        root = q.front();
        q.pop();
        levelOrder.push_back(node[root].val);
        if (node[root].l != -1)
            q.push(node[root].l);
        if (node[root].r != -1)
            q.push(node[root].r);
    }
}
int main()
{
    cin >> N;    
    int l, r;
    int root = 0;
    for (int i = 0; i < N; ++i)//按题目意思使用前序遍历构建一棵树
    {
        cin >> l >> r;
        node[i].l = l;
        node[i].r = r;
    }
    for (int i = 0; i < N; ++i)
        cin >> nums[i];
    sort(nums.begin(), nums.begin() + N);//得到中序遍历
    inOrderTravel(root);//通过中序遍历重构二叉树
    levelOrderTravel(root);
    for (int i = 0; i < N; ++i)
        cout << levelOrder[i] << (i == N - 1 ? "" : " ");
    return 0;
}