插入排序[数据结构]（复习）
主要由三个插入排序的重要算法：直接插入排序、折半插入排序和希尔排序。
其基本思想在于每次讲一个待排序的记录，按其关键字大小插入到前面已经排好序的子序列中，直到全部记录插入完成。
直接插入排序 稳定 O(n^2)
适用性：直接插入排序算法适用于顺序存储和链式存储的线性表。当为链式存储时，可以从前往后查找指定元素的位置
大部分排序算法都仅适用于顺序存储的线性表。
1 /** 2 * 插入排序 3 * 平均O(n^2),最好O(n),最坏O(n^2);空间复杂度O(1);稳定;简单 4 * @author zuo 5 * 6 */ 7 static void insertionSort(int[] a) { 8 int tmp; 9 for(int i=1;i<a.length;i++){ 10 for(int j=i;j>0;j--){ 11 if(a[j]<a[j-1]){ 12 tmp=a[j-1]; 13 a[j-1]=a[j]; 14 a[j]=tmp; 15 } 16 } 17 } 18 } 19 20 public static void main(String[] args) { 21 int array[] = {10,9,2,3,6,4,7,1,5,11,8}; 22 insertionSort(array); 23 for (int i : array) 24 System.out.print(i + " "); 25 }
初始： 10、9、2、3、6、4、7、1、5、11、8
第一趟：9、10、2、3、6、4、7、1、5、11、8
第二趟：2、9、10、3、6、4、7、1、5、11、8
第三趟：2、3、9、10、6、4、7、1、5、11、8
第四趟：2、3、6、9、10、4、7、1、5、11、8
第五趟：2、3、4、6、9、10、7、1、5、11、8
第六趟：2、3、4、6、7、9、10、1、5、11、8
第七趟：1、2、3、4、6、7、9、10、5、11、8
第八趟：1、2、3、4、5、6、7、9、10、11、8
第九趟：1、2、3、4、5、6、7、9、10、11、8
第十趟：1、2、3、4、5、6、7、8、9、10、11
折半插入排序
①每次插入，都从前面的有序子表中查找出待插入元素应该被插入的位置；
②给插入位置腾出空间，将待插入元素复制到表中的插入位置。
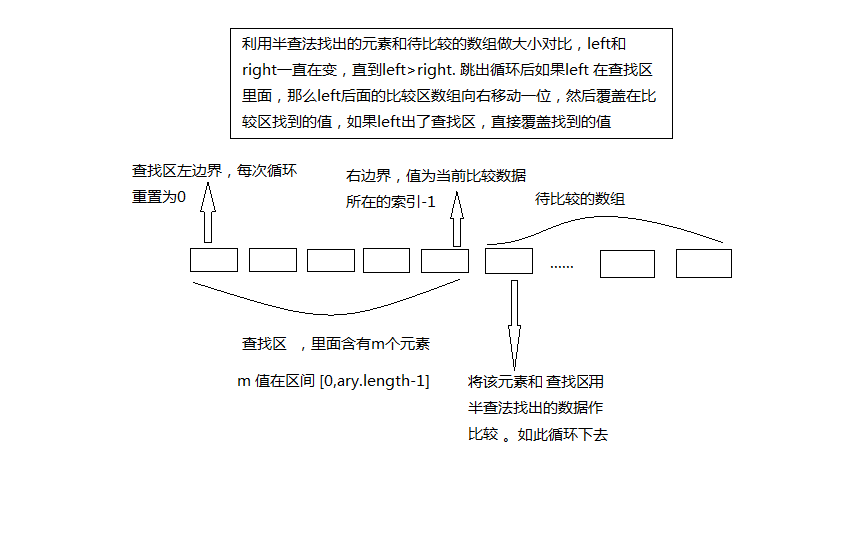
注意到该算法中，总是边比较边移动元素，下面将比较和移动操作分离开来，即先折半查找出元素的待插入位置，然后再同意地移动待插入位置之后的所有元素。当排序表为顺序存储的线性表时，可以对直接插入排序算法作如下改进：由于是顺序存储的线性表，所以查找有序子表时可以用折半查找来实现。在确定出待插入位置后，就可以统一地向后移动元素了。
1 /** 2 * 折半插入排序 3 * 折半查找只是减少了比较次数，但是元素的移动次数不变。 4 * 它的空间复杂度 O(1) ，时间复杂度O(n^2)，是一种稳定的排序算法 5 * @param data 6 * @author zuo 7 */ 8 static void binaryInsertSort(int[] data) { 9 for(int i=1;i<data.length;i++){ 10 if(data[i]<data[i-1]){ 11 int tmp=data[i];//缓存处的元素值 12 int low=0;//记录搜索范围的左边界 13 int high=i-1;//记录搜索范围的右边界 14 while(low<=high){ 15 int mid=(low+high)/2;//记录中间 16 if(data[mid]<tmp){//比较中间位置数据和处数据大小，以缩小搜索范围 17 low=mid+1; 18 }else{ 19 high=mid-1; 20 } 21 } 22 for(int j=i;j>low;j--){ 23 data[j]=data[j-1]; 24 } 25 data[low]=tmp; 26 print(data); 27 } 28 } 29 } 30 31 public static void main(String[] args) { 32 int array[] = {10,9,2,3,6,4,7,1,5,11,8}; 33 binaryInsertSort(array); 34 for (int i : array) 35 System.out.print(i + " "); 36 }
每一趟和直接插入排序相同。
性能分析:
折半查找只是减少了比较次数，但是元素的移动次数不变。约为O(nlog2n)，该比较次数与待排序表的初始状态无关，仅取决于表中的元素个数n；
而元素的异动次数没有变，它依赖于待排序表的初始状态，因此折半插入排序的时间复杂度仍为O(n^2)。
希尔排序
又称为缩小增量排序。
希尔排序的基本思想是：先将待排序表分割成若干个形如L[i,i+d,i+2d,...,i+kd]的“特殊”字表，分别进行直接插入排序；
然后取第二个步长d2<d1,重复上述过程，直到所取到的dt=1，即所有记录已放在同一组中，再进行直接插入排序，
由于此时已经具有较好的局部有序性，故可以很快得到最终结果。
1 static void shellSortSmallToBig(int[] data) { 2 int j = 0; 3 int temp = 0; 4 for (int increment = data.length / 2; increment > 0; increment /= 2) { 5 System.out.println("increment:" + increment); 6 for (int i = increment; i < data.length; i++) { 7 System.out.println("i:" + i); 8 temp = data[i]; 9 for (j = i - increment; j >= 0; j -= increment) { 10 System.out.println("j:" + j); 11 System.out.println("temp:" + temp); 12 System.out.println("data[" + j + "]:" + data[j]); 13 if (temp < data[j]) { 14 data[j + increment] = data[j]; 15 } else { 16 break; 17 } 18 } 19 data[j + increment] = temp; 20 } 21 for (int i = 0; i < data.length; i++) 22 System.out.print(data[i] + " "); 23 } 24 } 25 26 public static void main(String[] args) { 27 int array[] = {10,9,2,3,6,4,7,1,5,11,8}; 28 shellSortSmallToBig(array); 29 for (int i : array) 30 System.out.print(i + " "); 31 }
性能分析:
空间效率：仅使用了常数个辅助单元，空间复杂度为0(1)
时间效率：由于希尔排序的时间复杂度依赖于增量序列的函数，这涉及数学上还未解决的难题，所以其时间复杂度分析比较困难。当n在某个特定范围时，希尔排序的世界复杂度约为O(n^1.3)。在最坏情况下希尔排序的时间复杂度为O(n^2)。
稳定性：当相同关键字的记录被划分到不同字表时，可能会改变他们之间的相对次序，因此，希尔排序是一个不稳定的排序方法。
例如：表L={3,2,2}，经过一趟排序后，L={2，2，3},显然2与2的相对次序发生变化。
适用性：希尔排序算法仅适用于当线性表为顺序存储的情况。
