机器学习入门ONE——线性回归+Python用解析解的方式，模拟预测求解

前言：通过考研让我加深了对数学的理解，提升一小步数学思想，终于可以开始机器学习的新征程了。

刚学了线性回归、梯度下降和归一化。感觉考研数学一完全可以驾驭。目前....

求最大似然估计是每年数学一的必考题。

梯度下降也可以用导数知识轻松解释。

实时证明沉寂了一年多的我去考研，不碰代码。对我来说完全是个正确的决定。

 

 

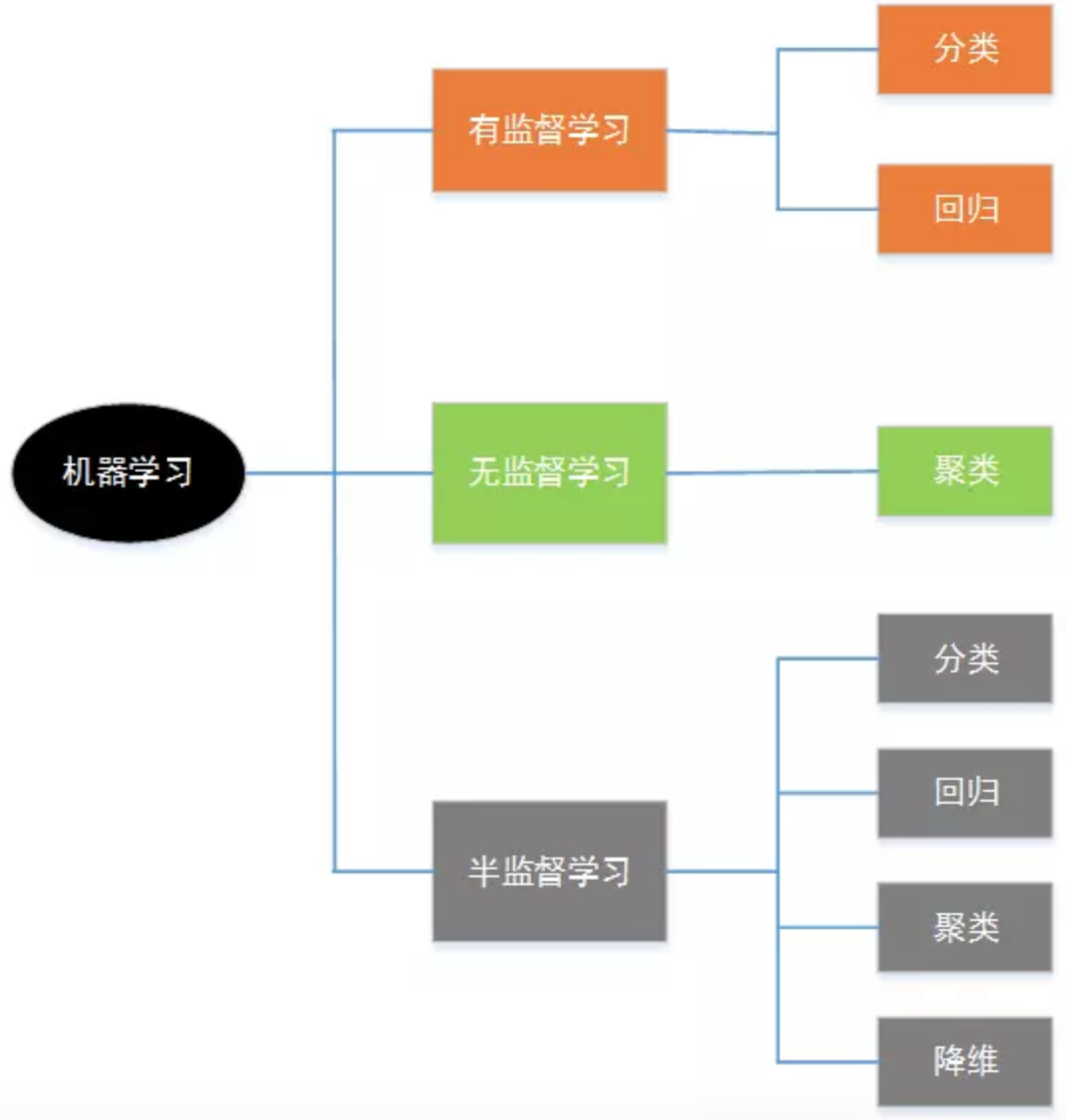
 线性回归

　　线性：y=a*x 一次方的变化
　　回归：回归到平均值

简单线性回归
　　算法==公式
　　一元一次方程组

　　一元指的一个X：影响Y的因素，维度

　　一次指的X的变化：没有非线性的变化

　　y = a*x + b
　　x1,y1 x2,y2 x3,y3 x4,y4 ...

 

做机器学习，没有完美解，只有最优解，做机器学习就是要以最快的速度，找到误差最小的最优解。

一个样本的误差：yi^ - yi　

找到误差最小的时刻，为了去找到误差最小的时刻，需要反复尝试，a,b根据最小二乘法去求得误差反过来误差最小时刻的a,b就是最终最优解模型

多元线性回归
　　本质上就是算法（公式）变换为了多元一次方程组 
　　y = w1*x1 + w2*x2 + w3*x3 + ... + wn*xn + w0*x0

总结问题
1、为什么求总似然的时候，要用正太分布的概率密度函数？
　　根据中心极限定理，如果假设样本之间是独立事件，误差变量随机产生，那么就服从正太分布

2、总似然不是概率相乘吗？为什么用了概率密度函数的f(xi)进行了相乘？
　　因为概率不好求，所以当我们可以找到概率密度相乘最大的时候，就相当于找到了概率相乘最大的时候

3、概率为什么不好求？
　　因为求得是面积，需要积分，麻烦

4、总似然最大和最优解得关系？
　　当我们找到可以使得总似然最大的条件，也就是可以找到我们的DataSet数据集最吻合某个正太分布
　　即找到了最优解

 

通过最大似然估计得思想，利用了正太分布的概率密度函数，推导出来了损失函数

1、何为损失函数？
　　一个函数最小，就对应了模型是最优解！预测历史数据可以最准！

2、线性回归的损失函数是什么？
　　最小二乘法，MSE，mean squared error，平方均值损失函数，均方误差

3、线性回归的损失函数有哪些假设？
　　样本独立，随机变量，正太分布

通过对损失函数求导，来找到最小值，求出theta的最优解

代码如下：

sklearn方法：

import numpy as np
from sklearn.linear_model import LinearRegression

X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

lin_reg = LinearRegression()
lin_reg.fit(X, y)  # 训练 求解模型
print(lin_reg.intercept_, lin_reg.coef_)

X_new = np.array([[0], [2]])
print(lin_reg.predict(X_new))

 

原始求解方法：

import numpy as np
import matplotlib.pyplot as plt

# rand均匀分布 随机x维度x1 返回一个均匀分布的随机数据
X = 2 * np.random.rand(100, 1)  # 100行1列的均匀分布数据  0-1之间  *2
# 人为设置真实的Y一列，randn 是标准正太分布，真实的y=预测的y+误差
# 4和3是模型  3=w1 4=w0
y = 4 * 1 + 3 * X + np.random.randn(100, 1)  # 100行1列的标准正态分布数据（误差）
# 记！ 解析解 =(X^T X)^-1 X^T y

# 整合X0和X1
X_b = np.c_[np.ones((100, 1)), X]  # c_ 是combine整合
# print(X_b)

# 常规等式求解theta   linalg线性代数  inv求逆
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
# print(theta_best)

# 创建测试集里面的X1
X_new = np.array([[0], [2]])
X_new_b = np.c_[(np.ones((2, 1))), X_new]
print(X_new_b)
y_predict = X_new_b.dot(theta_best)
print(y_predict)

plt.plot(X_new, y_predict, 'r-')
plt.plot(X, y, 'b.')
plt.axis([0, 2, 0, 15])
plt.show()