蓝桥杯练习 Day6 题解
蓝桥杯练习 Day6 题解
A
题意:给你一个等式ax+by = c,问你x,y是否有整数解。
思路:gcd(a,b) = t,如果方程有解,那么\((a/t)*x + (b/t)*y = c/t\)
方程\((a/t)*x + (b/t)*y=1\)是肯定有整数解的求得\(x'\),\(y'\),上式右边乘\((a/t)*x' + (b/t)*y'\)可求得\(x = (c/t)*x'\),那么\(x\)要为整数就必须有\(c/t\)为整数,及\(c\)能整除\(t\).
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
int gcd(int n,int m)
{
if(m == 0)
return n;
else return gcd(m,n%m);
}
int main(void)
{
int T,cn = 0;
scanf("%d",&T);
while(T--)
{
int n,m,c;
scanf("%d %d %d",&n,&m,&c);
LL gc = gcd(n,m);
printf("Case %d: ",++cn);
if(c%gc == 0)
printf("Yes\n");
else printf("No\n");
}
return 0;
}
B
题意:给\(N\)个球标号为\([1,N]\);从里面一下子抽取两个球,问这两个球上数字和小于\(k\)的概率;
思路:这题数据比较水暴力也能过。
先分\(k\)为奇偶讨论一下,如果k为偶数,\(cnt = (k-1)/2\);那么小于\(cnt\)的数和另一个数组合小于k的方案数为\(f-1\)(假设那个数为\(f\)),大于\(cnt\)的数和另一个数组合方案数为\((N-f)\)个,所以大于\(cnt\)和小于\(cnt\)两边的符合要求个数是对称的,那么总的符合要求的个数为\(a = (cnt + 1)*cnt\),当\(k\)为奇数时可以同样去推一下.总的方案数为\(b=N*(N-1)/2\),最后求下gcd化简下\((a/b)\).
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL gcd(LL n,LL m);
int main(void)
{
LL n,m;
while(scanf("%lld %lld",&n,&m),n!=-1&&m!=-1)
{
LL b = n*(n-1)/2;
LL a = 0;
if(m%2)
{
LL cnt = (m-1)/2;
a = ((LL)1+cnt)*cnt;
a -= cnt;
}
else
{ LL cnt = (m-1)/2;
a = ((LL)1+cnt)*cnt;
}
LL gc = gcd(a,b);
if(a == 0)printf("0\n");
else if(a == b)printf("1\n");
else
printf("%lld/%lld\n",a/gc,b/gc);
}
return 0;
}
LL gcd(LL n,LL m)
{
if(m == 0)return n;
else return gcd(m,n%m);
}
C
题意:从一个点开始,然后可以向六个方向走,然后问经过\(n\)步后从新回到开始的点的方案数有多少种.
思路:记忆化搜索;
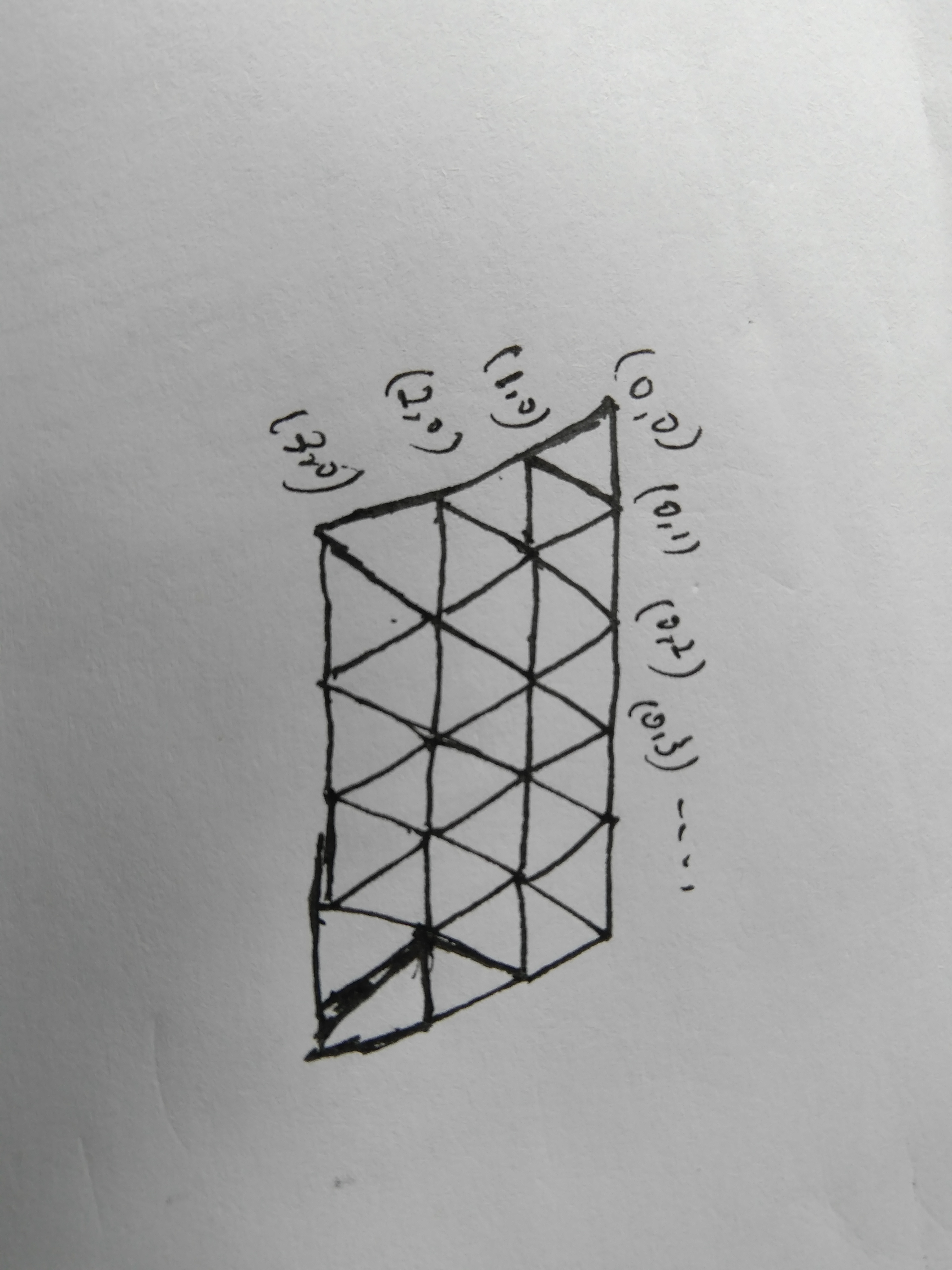
先取个起点(50,50),因为最多走14步,所以不可能超出边界.\(dp[n][m][k]\)表示走k步走到点\((n,m)\)的方案数,那么\(dp[n][m][k] = sum(dp[n+tx][m+ty][k-1])\) \(tx,ty\)表示的是6的不同方向上的对于当前点的增量。那么末状态为\(dp[n][m][k]\),然后记忆化搜索,复杂度为O(\(6*k^3\)).
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL dp[100][100][15];
int xx[6] = {0,-1,-1,0,1,1};//增量数组
int yy[6] = {-1,0,1,1,0,-1};
int slove(int n,int m,int k);
int main(void)
{
int T;
scanf("%d",&T);
while(T--)
{
int n;
scanf("%d",&n);
memset(dp,0,sizeof(dp));
int ask = slove(50,50,n);
ask = max(ask,0);
printf("%d\n",ask);
}
return 0;
}
int slove(int n,int m,int k)
{
if(dp[n][m][k] == -1)return -1;//当前状态不可到达
else if(dp[n][m][k])return dp[n][m][k];//当前状态可到达,如果已经被搜到过直接返回方案数
if(k == 1)//当k为1时只能在起始点的6个方向
{
if(n == 50&&m == 49)
return dp[n][m][k] = 1;
if(n == 49&&m == 50)
return dp[n][m][k] = 1;
if(n == 49&&m == 51)
return dp[n][m][k] = 1;
if(n == 50&&m == 51)
return dp[n][m][k] = 1;
if(n == 51&&m == 50)
return dp[n][m][k] = 1;
if(n == 51&&m == 49)
return dp[n][m][k] = 1;
else return dp[n][m][k] = -1;
}
int sum = 0;
for(int i = 0;i <= 5;i++)
{ int nx = n + xx[i];
int ny = m + yy[i];
int ask = slove(nx,ny,k-1);
if(ask!=-1)
{
sum += ask;
}
}
if(sum!=0)return dp[n][m][k] = sum;
else return dp[n][m][k] = -1;
}
D
题意:将给你的字串按要求输出.
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
char str[205];
char maxtr[20][20];
int main(void)
{
int n;
while(scanf("%d",&n),n!=0)
{
scanf("%s",str);
int l = strlen(str);
int cnt = 0,x = 0,y = 0;
for(int i = 0; i < l; i++)
{
maxtr[x][y] = str[i];
if(cnt%2)
{
y--;
if(y == -1)
y++,x++,cnt++;
}
else
{
y++;
if(y == n)
y--,x++,cnt++;
}
}
for(int j = 0; j < n; j++)
{
for(int i = 0; i < x; i++)
{
printf("%c",maxtr[i][j]);
}
}
printf("\n");
}
return 0;
}
E
题意:找出第\(k\)个立方的后三位是888的数.
思路:没思路打表找下规律,可以发现要找的数的末三为有4种可能s={\(192,442,692,942\)},那么4个一循环.让最后的解为\(head*1000 + t(t \in s)\),\(head\)开始为0,那么每4个过后\(head\)都加1.
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
void slove(LL n);
int table[4] = {942,192,442,692};
int main(void)
{
int T;
scanf("%d",&T);
while(T--)
{
LL n;
scanf("%lld",&n);
slove(n);
}
return 0;
}
void slove(LL n)
{
LL head = n/4;
if(n%4==0)head--;
head*=(LL)1000;
head += table[n%4];
printf("%lld\n",head);
}
F
题意:
问\([a,b]\)中的数的约数的个数为\(n\)的个数的个数.
因为\(b-a <= 10^4\),可以想到枚举约数\([1,sqrt(b)]\),然后开个数组记录在\([a,b]\)每个数的约数个数,复杂度O(\(sqrt(b)*log(b-a)\))
#include<bits/stdc++.h>
using namespace std;
int cnt[10005];
int main(void)
{
int a,b,n;
scanf("%d %d %d",&a,&b,&n);
for(int i = 1; i <= sqrt(b); i++)
{
for(int j = a/i; j <= b/i + 1; j++)
{
if(j*i >= a&&j*i <= b)
{
if(j<=sqrt(b))cnt[j*i-a]++;
else cnt[j*i-a] += 2;
}
}
}
int sum = 0;
for(int i = 0; i <= b-a; i++)
{
if(cnt[i] == n)
sum++;
}
printf("%d\n",sum);
return 0;
}
G
思路:根据题意可知没有环,可知任意两点之间若有路径,则经过的边数必不超过1,若超过1就不满足条件了。首先按给出的矩阵建图,然后对每个点bfs或dfs一次,判断是否有超过1的路径
#include <bits/stdc++.h>
using namespace std;
const int N = 2100;
vector<int> vec1[N], vec2[N];
int dis[N];
char str[N];
bool bfs(int s, vector<int> vec[])
{
queue<int> que;
memset(dis, 0, sizeof dis);
que.push(s);
while(! que.empty())
{
int v = que.front(); que.pop();
for(int i = 0; i < vec[v].size(); i++)
{
int u = vec[v][i];
if(dis[u] == 0)
{
if(v != s) return false;
dis[u] = dis[v] + 1, que.push(u);
if(dis[u] > 1) return false;
}
}
}
return true;
}
int main()
{
int t, n;
scanf("%d", &t);
while(t--)
{
scanf("%d", &n);
for(int i = 1; i <= n; i++)
{
scanf("%s", str+1);
for(int j = 1; j <= n; j++)
{
if(str[j] == 'P') vec1[i].push_back(j);
if(str[j] == 'Q') vec2[i].push_back(j);
}
}
bool flag = true;
for(int i = 1; i <= n; i++)
{
if(! bfs(i, vec1))
{
flag = false; break;
}
if(! bfs(i, vec2))
{
flag = false; break;
}
}
if(! flag) printf("N\n");
else printf("T\n");
for(int i = 1; i <= n; i++)
vec1[i].clear(), vec2[i].clear();
}
return 0;
}



