Robot(hdu5673)

Robot

Accepts: 92

Submissions: 188

Time Limit: 12000/6000 MS (Java/Others)

Memory Limit: 65536/65536 K (Java/Others)

问题描述

有一个机器人位于坐标原点上。每秒钟机器人都可以向右移到一个单位距离，或者在原地不动。如果机器人的当前位置在原点右侧，它同样可以
向左移动单位距离。一系列的移动（左移，右移，原地不动）定义为一个路径。问有多少种不同的路径，使得nnn秒后机器人仍然位于坐标原点？
答案可能很大，只需输出答案对1,000,000,0071,000,000,0071,000,000,007的模。

输入描述

输入包含多组数据. 第一行有一个整数T(1≤T≤100)T (1\leq T\leq 100)T(1≤T≤100), 表示测试数据的组数. 对于每组数据:
输入一个整数 n(1≤n≤1,000,000)n (1\leq n\leq 1,000,000)n(1≤n≤1,000,000)。

输出描述

对于每组数据，输出一个整数

输入样例

3
1
2
4

输出样例

1
2
9

思路：默慈金数

在一个网格上，若限定每步只能向右移动一格，可以右上，右下，

横向，向右，并禁止移动到以下的地方，则以这种走法移动步从到的可能形成的路径的总数

为的默慈金数。如下图示

 

         

 

默慈金数满足如下递推式：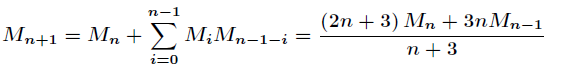 
可以将点的过程想象成上图，那么就是一个很裸的默慈金数；

#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<string.h>
#include<queue>
#include<set>
#include<math.h>
#include<map>
const int N =1e9+7;
using namespace std;
typedef long long LL;
LL quick(LL n,LL m,LL mod);
LL M[1000005];
int main(void)
{
    M[1] = 1;M[0] = 1;int i;
    for(i = 2;i <= 1000000;i++)
    {
       LL x = (2*i+1)*M[i-1]%N;
       LL y = (3*i-3)*M[i-2]%N;
       x = (x+y)%N;
       y = i+2;
       LL ni = quick(y,N-2,N);
       //printf("%lld\n",ni);
       M[i] = x*ni%N;
    }
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int n;
        scanf("%d",&n);
        printf("%lld\n",M[n]);
    }
    return 0;
}
LL quick(LL n,LL m,LL mod)
{
    n%=mod;
    LL ask = 1;
    while(m)
    {
        if(m&1)
            ask = ask*n%mod;
        n = n*n%mod;
        m>>=1;
    }
    return ask;
}