Grids
Grids
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 717 Accepted Submission(s): 296
Problem Description
度度熊最近很喜欢玩游戏。这一天他在纸上画了一个2行N列的长方形格子。他想把1到2N这些数依次放进去,但是为了使格子看起来优美,他想找到使每行每列都递增的方案。不过画了很久,他发现方案数实在是太多了。度度熊想知道,有多少种放数字的方法能满足上面的条件?
Input
第一行为数据组数T(1<=T<=100000)。
然后T行,每行为一个数N(1<=N<=1000000)表示长方形的大小。
然后T行,每行为一个数N(1<=N<=1000000)表示长方形的大小。
Output
对于每组数据,输出符合题意的方案数。由于数字可能非常大,你只需要把最后的结果对1000000007取模即可。
Sample Input
2
1
3
Sample Output
Case #1:
1
Case #2:
5
Hint
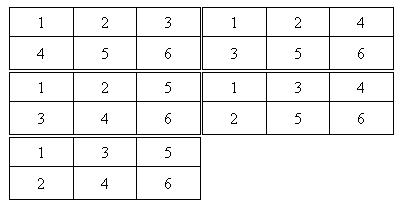
对于第二组样例,共5种方案,具体方案为:
Source
思路:卡特兰数+费马小定理求逆元;
为啥是卡特兰数,我们把第一行看成是入栈,第二行看成是出栈,那么观察下1只能放在第一,接下来我们需要放2,2可以放在2个位置,1.放在1的下边,那么此时3就只能放在第一行的第二个,这就表示1出栈了,那么3需要进栈,2.放在第一行的第二个的话,那么3可以放在1的下端,也可以放在第一行的第3个.....
那么我们从中可以知道只要队列不空那么当前的数就可以放在下边,并且是下边没放的第一个,这样后来的数大,就保证了升序合法,同样放上面也是这个原则,所以这个就和火车入栈出栈一样,是卡特兰数的应用。然后递推下卡特兰数,取模时费马小定理求下逆元即可。
1 #include<stdio.h> 2 #include<algorithm> 3 #include<iostream> 4 #include<string.h> 5 #include<queue> 6 #include<stack> 7 #include<set> 8 #include<math.h> 9 using namespace std; 10 typedef long long LL; 11 const int N=1e9+7; 12 LL dp[1000005]; 13 LL quick(LL n,LL m); 14 int main(void) 15 { 16 int i,j,k; 17 dp[1]=1; 18 dp[2]=2; 19 dp[3]=5; 20 for(i=4; i<=1000000; i++) 21 { 22 dp[i]=dp[i-1]*(4*i-2)%N; 23 dp[i]=dp[i]*quick((LL)(i+1),N-2)%N; 24 } 25 scanf("%d",&k); 26 int s; 27 int t; 28 for(s=1; s<=k; s++) 29 { 30 scanf("%d",&t); 31 printf("Case #%d:\n",s); 32 printf("%lld\n",dp[t]); 33 } 34 return 0; 35 } 36 LL quick(LL n,LL m) 37 { 38 LL ak=1; 39 while(m) 40 { 41 if(m&1) 42 { 43 ak=ak*n%N; 44 } 45 n=(n*n)%N; 46 m/=2; 47 } 48 return ak; 49 }
油!油!you@



