A. Watchmen(Codeforces 650A)

A. Watchmen

time limit per test
3 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

Watchmen are in a danger and Doctor Manhattan together with his friend Daniel Dreiberg should warn them as soon as possible. There are n watchmen on a plane, the i-th watchman is located at point (xi, yi).

They need to arrange a plan, but there are some difficulties on their way. As you know, Doctor Manhattan considers the distance between watchmen i and j to be |xi - xj| + |yi - yj|. Daniel, as an ordinary person, calculates the distance using the formula .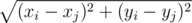

The success of the operation relies on the number of pairs (i, j) (1 ≤ i < j ≤ n), such that the distance between watchman i and watchmen j calculated by Doctor Manhattan is equal to the distance between them calculated by Daniel. You were asked to compute the number of such pairs.

Input

The first line of the input contains the single integer n (1 ≤ n ≤ 200 000) — the number of watchmen.

Each of the following n lines contains two integers xi and yi (|xi|, |yi| ≤ 109).

Some positions may coincide.

Output

Print the number of pairs of watchmen such that the distance between them calculated by Doctor Manhattan is equal to the distance calculated by Daniel.

Examples
input
3
1 1
7 5
1 5
output
2
input
6
0 0
0 1
0 2
-1 1
0 1
1 1
output
11
Note

In the first sample, the distance between watchman 1 and watchman 2 is equal to |1 - 7| + |1 - 5| = 10 for Doctor Manhattan and 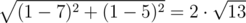 for Daniel. For pairs (1, 1), (1, 5) and (7, 5), (1, 5) Doctor Manhattan and Daniel will calculate the same distances.

思路：Manhattan and Daniel will calculate the same distances曼哈顿距离和两点间的距离相等，A（x1，y1） ，B（X2，Y2）；

|x1-x2|+|y1-y2|=sqrt((x1-x2)^2+(y1-y2)^2);

画个三角形你可以发现曼哈顿距离就是两直角边的和，而两点的距离为斜边

那么当且x1==x2||y1==y2;这两种距离相等

 

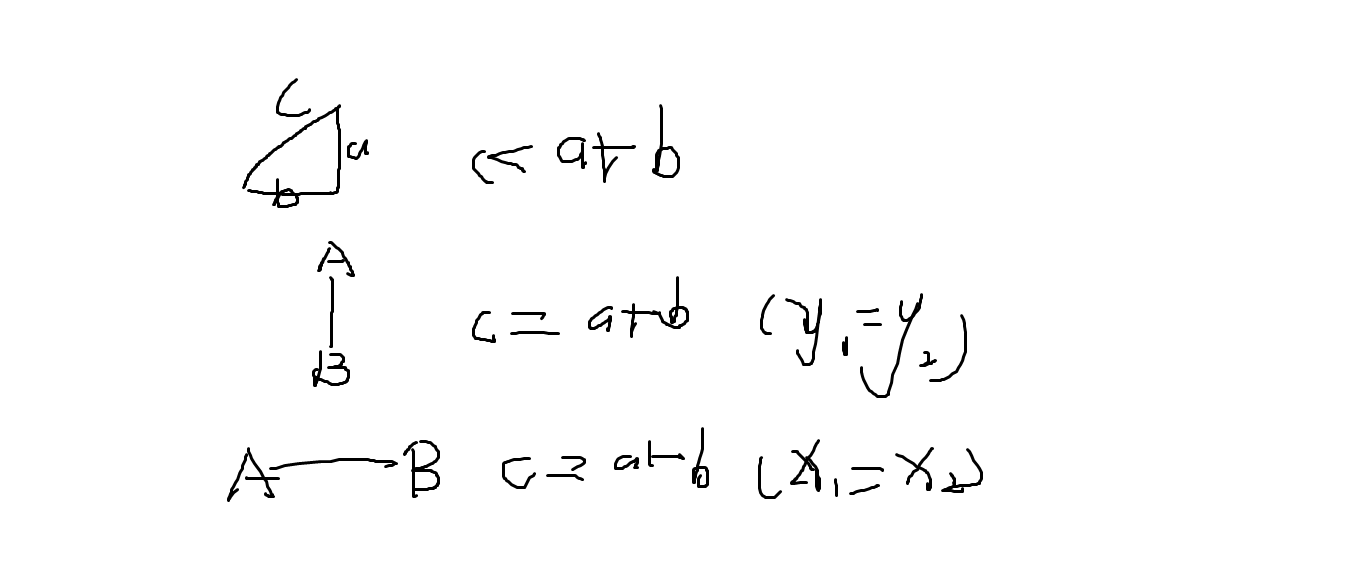
那么只要找x1==x2||y1==y2，开个数组记录各个x的种类及其个数，y的种类和个数，c[x]，b[y]，由于x和y的数值比较大所以离散化下可以。

sum+=c[x]*（c[x]-1）/2（c[x]〉=1）；sum+=c[y]*（c[y]-1）/2；最如果点相同这样算就相当重复算了一遍，所以只要再找出那些相同的点，以及种类个数

R[i]；ans+=（R[i]*（R[i]-1）/2；最后答案就是sum-ans；

  1 #include<stdio.h>
  2 #include<algorithm>
  3 #include<iostream>
  4 #include<stdlib.h>
  5 #include<string.h>
  6 #include<map>
  7 #include<queue>
  8 #include<math.h>
  9 #include<set>
 10 #include<stack>
 11 #include<map>
 12 int cmp(const void*p,const void*q);
 13 using namespace std;
 14 typedef long long LL;
 15 typedef struct pp
 16 {
 17     LL x;
 18     LL y;
 19 } ss;
 20 ss aa[200005*4];LL bb[200005*4];
 21 ss ak[200005*4];ss bk[200005*4];
 22 LL cc[4*200005];LL yy[200005*4];
 23 LL vv[200005*4];
 24 typedef pair<int,int> P;
 25 int main(void)
 26 {
 27    LL i,j,k,p,q;
 28   scanf("%I64d",&k);
 29    {   LL cnt=0;LL x,y;memset(vv,0,sizeof(vv));
 30       map<P,LL>my;memset(yy,0,sizeof(yy));my.clear();
 31        for(i=0;i<k;i++)
 32        {
 33            scanf("%I64d %I64d",&x,&y);
 34             bb[cnt++]=x;
 35             bb[cnt++]=y;
 36        }
 37        for(i=0;i<cnt;i++)
 38        {
 39            aa[i].x=bb[i];
 40            aa[i].y=i;
 41        }
 42        qsort(aa,cnt,sizeof(ss),cmp);
 43        cc[0]=0;LL ans=0;
 44        for(i=1;i<cnt;i++)
 45        {
 46            if(aa[i].x!=aa[i-1].x)
 47            ans++;
 48            cc[aa[i].y]=ans;
 49        }LL uu=0;
 50        for(i=0;i<cnt;i++)
 51        {
 52            if(i%2==0)
 53            {
 54                ak[uu].x=cc[i];
 55            }
 56            else {ak[uu].y=cc[i];uu++;}
 57        }LL rns=0;LL bbq=1;
 58        for(i=0;i<uu;i++)
 59        {P l;l.first=ak[i].x;l.second=ak[i].y;
 60            if(my[l]==0)
 61            {
 62                my[l]=bbq++;
 63            }
 64        }for(i=0;i<uu;i++)
 65        {P l;l.first=ak[i].x;l.second=ak[i].y;
 66            vv[my[l]]++;
 67        }
 68        LL an=0;
 69        for(i=1;i<bbq;i++)
 70        {
 71            if(vv[i]>=2)
 72            {
 73                an+=vv[i]*(vv[i]-1)/2;
 74            }
 75        }
 76        for(i=0;i<uu;i++)
 77        {
 78            yy[ak[i].x]++;
 79        }LL sum=0;
 80        for(i=0;i<500005;i++)
 81        {
 82            if(yy[i]>=2)
 83            {
 84                sum+=yy[i]*(yy[i]-1)/2;
 85            }
 86        }memset(yy,0,sizeof(yy));
 87        for(i=0;i<uu;i++)
 88        {
 89            yy[ak[i].y]++;
 90        }
 91          for(i=0;i<500005;i++)
 92        {
 93            if(yy[i]>=2)
 94            {
 95                sum+=yy[i]*(yy[i]-1)/2;
 96            }
 97        }
 98        printf("%I64d\n",sum-an);
 99    }
100    return 0;
101 }
102 
103 int cmp(const void*p,const void*q)
104 {
105     ss*nn=(ss*)p;
106     ss*mm=(ss*)q;
107     return nn->x-mm->x;
108 }

 

posted @ 2016-03-07 22:34  sCjTyC  阅读(908)  评论(0)  编辑  收藏  举报