二叉树

二叉树

• 根节点：树中上部的节点
• 左叶子节点
• 右叶子节点
• 子树
  • 完整的子树
    • 一个根节点，左右叶子节点组成
  • 不完整的子树
    • 根节点，左叶子节点
    • 根节点，右叶子节点
    • 根节点
      • 特点：每一个节点都可以作为某一颗子树的根节点

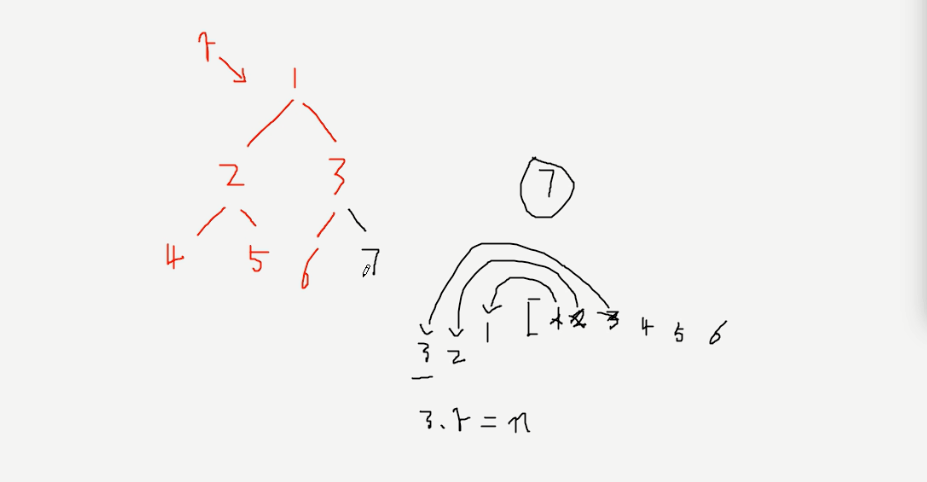
构造二叉树

• 想法：创建列表，每次循环判断节点的left和right，如果不为空将该节点放入列表，用于下次pop(0)取出节点再次判断，如果没空插入即可

  class Node():
      def __init__(self,item):
          self.item = item
          self.left = None #指向该节点的左叶子节点
          self.right = None#指向该节点的右叶子节点
  class Tree():
      def __init__(self):#构建一颗空树
          self.root = None #永远指向二叉树中的根节点
      #自上到下从左到右的准则插入新的节点
      def insert(self,item):#向树种插入一个节点
          node = Node(item)
          #如果树为空
          if self.root == None:
              self.root = node
              return
          #如果树为非空
          cur = self.root
          q = [cur]
          while True:
              n = q.pop(0)
              if n.left != None:
                  q.append(n.left)
              else:
                  n.left = node
                  break
              if n.right != None:
                  q.append(n.right)
              else:
                  n.right = node
                  break
                  
      #广度遍历
      def travel(self):
      	 if self.root == None:
           	return
          cur = self.root
          q = [cur]
          while q:
              n = q.pop(0)
              print(n.item)
              if n.left != None:
                  q.append(n.left)
              if n.right != None:
                  q.append(n.right)
  
  #                
  tree = Tree()
  tree.insert(1)
  tree.insert(2)
  tree.insert(3)
  tree.insert(4)
  tree.insert(5)
  tree.insert(6)
  tree.travel()
  

  结果：1 2 3 4 5 6
  

  二叉树的遍历

  • 广度遍历
    • 上述代码中的遍历，就是广度遍历。自上到下逐行遍历叫做广度遍历。
    • 横向遍历
  • 深度遍历：纵向遍历。前中后序遍历形式需要作用到子树中。前中后序中的前中后指的是子树中根节点的位置（递归）
    • 前序：根左右，先遍历子树的根节点，在遍历子树的左节点然后是右节点
    • 中序：左根右
    • 后序：左右根

前中后序遍历形式需要作用到子树中，需要我们传入根节点
#前序遍历
    #参数root表示的是子树的根节点，需要给递归调用的forward传入不同子树的根节点
    def forward(self,root):#根左右
        if root == None:
            return
        print(root.item)
        self.forward(root.left)
        self.forward(root.right)

    def middle(self,root):#左跟右
        if root == None:
            return
        self.middle(root.left)
        print(root.item)
        self.middle(root.right)
    def back(self,root):#左右根
        if root == None:
            return
        self.back(root.left)
        self.back(root.right)
        print(root.item)
        

前序结果：

1 2 4 5 3 6 7

中序结果：

4 2 5 1 6 3 7

后序结果：

4 5 2 6 7 3 1

深度遍历的实现思路

• 深度遍历是需要作用到每一颗子树中
• 子树和子树之间的区别体现在根节点中。
• 如果写一个函数，该函数可以将一个子树中的节点进行遍历，则将该函数作用到其他子树中就可以将整棵树进行深度遍历。

排序二叉树

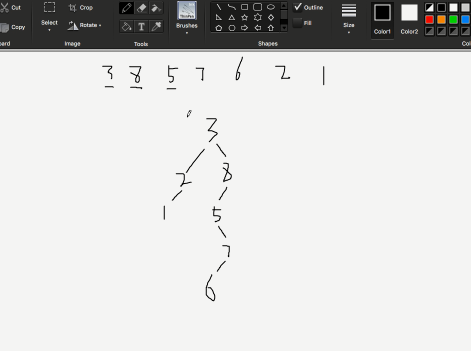
• 排序二叉树用中序遍历，获取有序序列！

• class Node():
      def __init__(self,item):
          self.item = item
          self.left = None #指向该节点的左叶子节点
          self.right = None#指向该节点的右叶子节点
  class SortTree():
      def __init__(self):
          self.root = None
      def add(self,item):#将节点插入到排序二叉树中
          node = Node(item)
          if self.root == None: #树为空的情况
              self.root = node
              return
          cur = self.root
          while True:
              #树为非空
              if cur.item > item:#插入的节点值小于根节点，该节点需要插入到根节点的左侧
                  if cur.left == None:#如果左节点为空，则直接插入
                      cur.left = node
                      break
                  else:#左节点为非空
                      cur = cur.left
              else: #插入节点的值大等于于根节点，该节点需要插入到根节点的右侧
                  if cur.right == None:
                      cur.right = node
                      break
                  else:
                      cur = cur.right
      def middle(self,root):#左跟右
          if root == None:
              return
          self.middle(root.left)
          print(root.item)
          self.middle(root.right)
  

  alist = [3,8,5,7,6,2,1]
  tree = SortTree()
  for item in alist:
      tree.add(item)
  tree.middle(tree.root)
  
  #结果：
  1 2 3 5 6 7 8