第七章学习小结

本章学习了三种不同结构的查找表：线性表、树表和散列表。查找的术语包括：查找表、关键字（主关键字、次关键字）、查找（查找成功、查找不成功）、动态查找表和静态查找表、平均查找长度（ASL）

（一）线性表的查找

1、顺序查找

typedef struct   //数据元素类型定义 
{
    KeyType key;    
    InfoType otherinfo;    
}ElemType;
typedef struct   //顺序表的定义
{
    ElemType *R;    //基地址
    int length;    
}SSTable;

//查找 
int Search_Seq(SSTable ST, KeyType key)
{
    for(i=ST.length; i>=1; --i)
           if(ST.R[i].key==key)      
               return i;   //从后往前找
    return 0;
}
//or设置监视哨的顺序查找
int Search_Seq(SSTable ST, KeyType key)
{
    ST.R[0].key=key;   //“哨兵”
    for(i=ST.length; ST.R[i].key!=key; --i)
    return i;  
}

时间复杂度为O(n)，空间复杂度为O(1)。

优点：对表结构无任何要求，既适用于顺序结构，也适用于链式结构，无论记录是否按关键字有序均可应用。

缺点：平均查找长度较大，查找效率较低，所以当n很大时，不宜采用顺序查找。

习题：

n个数存在一维数组A[1...n]中，在进行顺序查找时，这n个数的排列有序或无序其平均查找长度ASL不同。----正确

析：查找概率相等时，ASL相同；查找概率不等时，如果从前向后查找，则按查找概率由大到小排列的有序表其ASL要比无序表ASL小。

2、折半查找/二分查找

//非递归算法 
int Search_Bin(SSTable ST, KeyType key)
{
    low=1;   high=ST.length;    
    while(low<=high)
    {
        mid=(low+high)/2;    
        if(key==ST.R[mid].key)    return mid;   
        else if(key<ST.R[mid],key)    high=mid-1;    //前一子表查找
        else   low=mid+1;     //后一子表查找
    }
    return 0;  
}
//递归算法
int Search_Bin(SSTable ST, KeyType key, int low, int high)
{
    if(low>high)     
        return 0;
    mid=(low+high)/2;
    if(key==ST.elem[mid].key)    
        return mid;
    else if(key<ST.elem[mid].key)
        return Search_Bin(ST, key, low, mid-1)   //递归
    else   
        return Search_Bin(ST, key, mid+1, high)    //递归
}

时间复杂度为O(log₂n)。

优点：比较次数少，查找效率高。

缺点：对表结构要求高，只能用于顺序存储的有序表。查找前需要排序。不适用于数据元素经常变动的线性表。

3、分块查找/索引顺序查找

特点：块间有序，块内无序

查找效率：ASL=L_b+L_w 。L_b ：对索引表查找的ASL；L_w ：对块内查找的ASL。

查找块：顺序查找 Or 折半查找（更优）；块内查找：顺序查找。

优点：由于块内是无序的，故插入和删除比较容易，无需进行大量移动。如果线性表既要快速查找又经常动态变化，则可采用分块查找。

缺点：要增加一个索引表的存储空间并对初始索引表进行排序运算。

（二）树表的查找

1、二叉排序树

空树 Or 具有下列性质的二叉树：

(1)若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

(2)若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

(3)它的左、右子树也分别为二叉排序树。

二叉排序树是递归定义的。一个重要性质：中序遍历一棵二叉树时可以得到一个结点值递增的有序序列。

typedef struct    //结点的数据域结构
{
    KeyType key;    
    InfoType otherinfo; 
}ElemType;   
typedef struct BSTNode   //结点结构
{
    ElemType data;   
    struct BSTNode *lchild, *rchild;   
}BSTNode, *BSTree;

//递归查找
BSTree SearchBST(BSTree T, KeyType key)
{
    if((!T)||key==T->data.key)   return T;     
    else if(key<T->data.key)   return SearchBST(T->lchild, key);  
    else  return SearchBST(T->rchild, key);    
}

//插入--插入的元素一定在叶结点上
void InsertBST(BSTree &T, ElemType e)
{
    if(!T)
    {//找到插入位置，递归结束
        S=new BSTNode;     //生成新结点*S
        S->data=e;      //新结点*S的数据域置为e
        S->lchild=S->rchild=NULL;    //新结点*S作为叶子结点
        T=S;     //把新结点*S链接到已找到的插入位置
    }
    else if(e.key<T->data.key)
          InsertBST(T->lchild, e);      //将*S插入左子树
    else if(e.key>T->data.key)
          InsertBST(T->rchild, e);      //将*S插入右子树
}

//创建
void CreateBST(BSTree &T)
{//依次读入一个关键字为key的结点，将此结点插入二叉排序树T中
    T=NULL;      //将二叉排序树T初始化为空树
    cin>>e;  
    while(e.key!=ENDFLAG)     //ENDFLAG为自定义常量，作为输入结束标志
    {
        InsertBST(T, e);     //将此结点插入二叉排序树T中
        cin>>e; 
    }  
}

//删除
void DeleteBST(BSTree &T, KeyType key)
{//从二叉排序树T中删除关键字等于key的结点
    p=T;  f=NULL;    //初始化
    /*------下面的while循环从根开始查找关键字等于key的结点*p------*/
    while(p)
    {
        if(p->data.key==key)   break;//找到关键字等于key的结点*p
        f=p;     //*f为*p的双亲结点
        if(p->data.key>key)   p=p->lchild;  //在*p的左子树中继续查找
        else p=p->rchild;     //在*p的右子树中继续查找
    }
    if(!p)      return;    //找不到被删结点则返回
    /*---考虑3种情况实现p所指子树内部的处理：*p左右子树均不空、无右子树、无左子树-----*/
    if((p->lchild)&&(p->rchild))     //被删结点*p左右子树均不空
    {
        q=p;  s=p->lchild;
        while(s->rchild)
        //在*p的左子树中继续查找其前驱家电，即最右下结点
        {
            q=s;  s=s->rchild;   //向右到尽头
        }
        p->data=s->data;     //s指向被删结点的“前驱”
        if(q!=p)    q->rchild=s->lchild;     //重接*q的右子树
        else  q->lchild=s->lchild;     //重接*q的左子树
        delete s;
        return;
    }
    else if(!p->rchild)    //被删结点*p无右子树，只需重接其左子树
    {
        q=p;   p=p->lchild;    delete q;
    }
    else if(!p->lchild)    //被删结点*p无左子树，只需重接其右子树
    {
        q=p;   p=p->rchild;   delete q;
    }
    /*---将p所指的子树挂接到其双亲结点*f相应的位置---------*/
    if(!f)    T=p;    //被删结点为根结点
    else if(q=f->lchild)    f->lchild=p;    //挂接到*f的左子树位置 
    else  f->rchild=p;    //挂接到*f的右子树位置
    delete q;    
}

查找的时间复杂度为 O(log₂n)，而插入和删除的基本操作也是查找，时间复杂度均为O(log₂n)。创建的时间复杂度为 O(nlog₂n)。

查找性能分析：

平均查找长度和二叉树的形态有关，即

最好：log₂n（形态匀称，与二分查找的判定树相似）

最坏:（n+1)/2（单支树）

2、平衡二叉树（AVL树）

空树 Or 具有如下特征的二叉排序树：

(1)左子树和右子树的深度之差的绝对值不超过1;

(2)左子树和右子树也是平衡二叉树。 

平衡因子只可能是-1、0和1。

深度和log₂n是同数量级的（其中n为结点个数）。由此，其查找的时间复杂度是O(log₂n)。

平衡二叉树的平衡调整方法：LL、RR、LR、RL。

对于同样的数据量，二叉查找树的深度大，而多叉树的深度小，因此多叉树适用于要求查找深度小的检索。

3、B树（多叉树）：B-树和B+树

特点：平衡、有序、多路

（三）散列表的查找

散列查找法又叫杂凑法或散列法。

优点：查找速度极快O(1)，查找效率与元素个数n无关。

1、术语：

散列函数（哈希函数）和散列地址：p=H(key),称这个对应关系H为散列函数，p为散列地址。H函数称为哈希函数。

散列表：一个有限连续的地址空间，用以存储按散列函数计算得到相应散列地址的数据记录。通常散列表的存储空间是一个一维数组，散列地址是数组的下标。

冲突：对不同的关键字可能得到同一散列地址。

同义词：具有相同函数值的关键字。

2、散列函数的构造方法

(1)数字分析法：适合于能预先估计出全体关键字的每一位上各种数字出现的频度。

(2)平法取中法：适合于关键字中每一位都有某些数字重复出现频度很高的现象。

(3)折叠法：适合于关键字的数字位数特别多。

(4)除留余数法：Hash(key)=key mod p(p是一个整数)

一般情况下，可以选p为小于表长的最大质数。

3、处理冲突的方法

(1)开放地址法：H_i=(H(key)+d_i) MOD m       i=1,2,…，k(k≦m-1)

其中，H(key)为散列函数，m为散列表表长，d_i为增量序列。根据d_i取值的不同，可以分为以下3种探测方法：

A.线性探测法：d_i=l,2,3,…,m-1

B.二次探测法：d_i=1²,-1²,2²,-2²,3²,…,+k²,-k²(k≦m/2)

C.伪随机探测法：d_i=伪随机数序列

优点：只要散列表未填满，总能找到一个不发生冲突的地址。

缺点：会产生“二次聚集”现象。而二次探测法和伪随机探测法的优点是：可以避免“二次聚集”现象。缺点也很显然：不能保证一定找到不发生冲突的地址。

(2)链地址法（拉链法）

优点：非同义词不会冲突，无“聚集”现象；链表上结点空间动态申请，更适合于表厂不确定的情况。

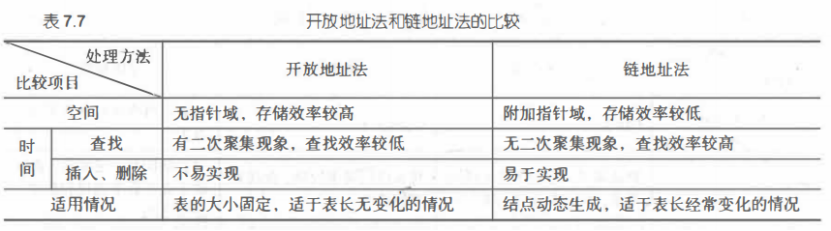
4、ASL的决定因素：散列函数、处理冲突的方法和散列表的装填因子α（α=表中填入的记录数/散列表的长度）。 

散列表的ASL是处理冲突方法和装载因子的函数。

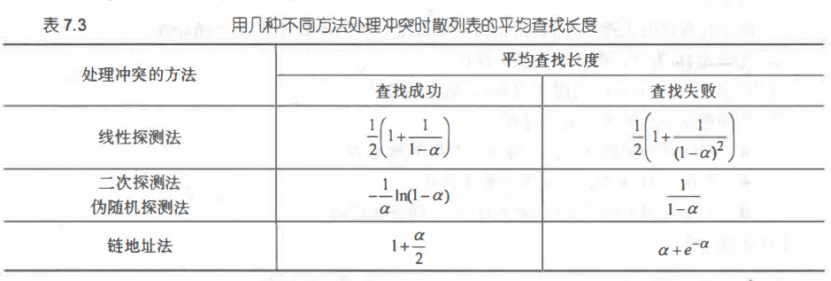
哈希表的平均查找长度是α的函数，而不是n的函数。

哈希表所特有的特点：用哈希表构造查找表时，可以选择一个适当的装填因子α，使得平均查找长度限定在某个范围内。

关于哈希查找的几点结论： 

1.哈希表技术具有很好的平均性能，优于一些传统的技术

2.链地址法优于开地址法

3.除留余数法作哈希函数优于其它类型函数