堆排序 Heapsort

堆排序：

由三个函数组成：

Max_heapify ( int A[] ,int i ,int heap_size)//堆化  T(n)=log(n);

Build_max_heap(int A[],int heap_size)//建堆   T(n)=n ;

Heap_sort(int A[],int length)//排序 T(n)=n*log(n);

#include<stdio.h>
//#include<stdlib.h>

void PrintArray(int data[] ,int length){
    int i;
    for(i=0;i<length;i++){
        printf("%d ",data[i]);
    }
    printf("\n");
}

//heap_size;堆的大小
// 堆化，保持堆的性质
// Max_Heapify让A[i]在最大堆中"下降"，
// 使以i为根的子树成为最大堆
void Max_heapify( int A[] ,int i ,int heap_size){
    int l=2*i+1;//左子树下标
    int r=2*i+2;//右子树下标
    int largest,t;
    if(l<heap_size&&A[l]>A[i]){
        largest=l;
    }
    else largest=i;
    if(r<heap_size&&A[r]>A[largest]){
        largest=r;
    }
    if(largest!=i){
        t=A[i];    
        A[i]=A[largest];
        A[largest]=t;
        Max_heapify(A,largest,heap_size);
    }
}

// 建堆
// 自底而上地调用MaxHeapify来将一个数组a[1..size]变成一个最大堆
Build_max_heap(int A[],int heap_size){
    int i;
    for(i=heap_size/2;i>=0;i--){
        Max_heapify(A,i,heap_size);
    }
}

// 堆排序
// 初始调用BuildMaxHeap将a[1..size]变成最大堆
// 因为数组最大元素在a[1]，则可以通过将a[1]与a[size]互换达到正确位置
// 现在新的根元素破坏了最大堆的性质，所以调用MaxHeapify调整，
// 使a[1..size-1]成为最大堆，a[1]又是a[1..size-1]中的最大元素，
// 将a[1]与a[size-1]互换达到正确位置。
// 反复调用Heapify，使整个数组成从小到大排序。
// 注意： 交换只是破坏了以a[1]为根的二叉树最大堆性质，它的左右子二叉树还是具备最大堆性质。
//        这也是为何在BuildMaxHeap时需要遍历size/2到1的结点才能构成最大堆，而这里只需要堆化a[1]即可
Heap_sort(int A[],int length){
    int i,t;
    int heap_size=length;
    Build_max_heap(A,length);
    printf("初始最大堆：\n");
    PrintArray(A,length);
    for(i=length-1;i>=1;i--){
        t=A[i];
        A[i]=A[0];
        A[0]=t;
        heap_size--;
        Max_heapify(A,0,heap_size);
        printf("中间过程：\n");
        PrintArray(A,length);
    }
}



void main(){
    int A[]={4,6,1,8,15,2,17,9,3};
    int length=sizeof(A)/sizeof(A[0]);
    Heap_sort(A,length);
    printf("\n最后结果：\n");
    PrintArray(A,length);
}

结果：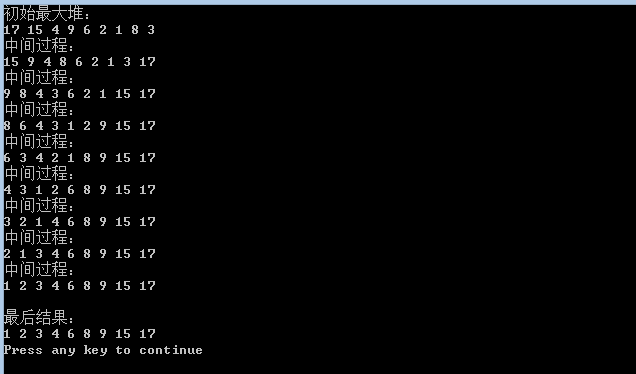

时间复杂度为：n*logn