C#实现有向无环图(DAG)拓扑排序
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序.
线性结构概念
总的来说,“线性结构”是一个有序数据元素的集合 线性结构满足以下特点:
- 集合中必存在唯一“第一个元素”;
- 集合中必存在唯一“最后一个元素”;
- 除了最后一个元素,所有元素均有唯一“后继结点”;
- 除了第一个元素,所有元素均有唯一“前趋结点”
和我们abp Module很像,第一个加载模块永远是其ABP核心模块,最后一个模块永远是我们的启动模块
举例
1.大学课程排序
大学课程的学习是有先后顺序的,C语言是基础,数据结构依赖于C语言,其它课程也有类似依赖关系。这样的一个课程安排是怎么实现的呢?
2.VS项目编译顺序
假设VS中有三个项目A,B,C,它们的关系如下。VS编译器是如何判断三个项目的编译顺序的呢?
A->B->C A引用B B引用C
A->B->C->A 提示循环引用
ABP的Module
ABP中的模块也是如此,不可循环引用相互依赖A->B B->A X
前面说到ABP中的第一个模块和最后一个模块是确定的。
呢么中间的是怎么排序的呢。其实用的是拓扑算法
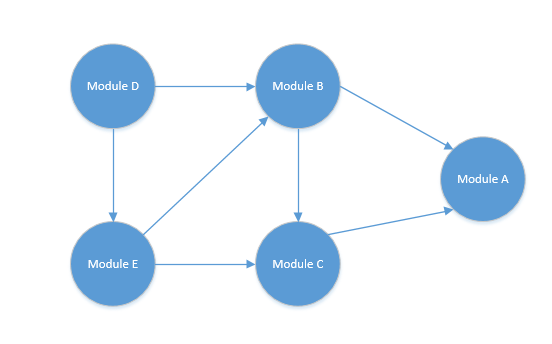
从图中可以得知:
1.A模块是最核心的,不依赖于其他任何模块
2.D依赖E和B,E依赖B和C,B依赖C和A,C依赖A
那么根据拓扑排序,应该如何排序呢?
1.从图中找一个没有前驱指向它的顶点
2.删除该顶点.以及该顶点的前驱
3.重复步骤 1 and 2 ,直到图中顶点为空 或者 找不到步骤1中这样的顶点 为止.
排序如下:
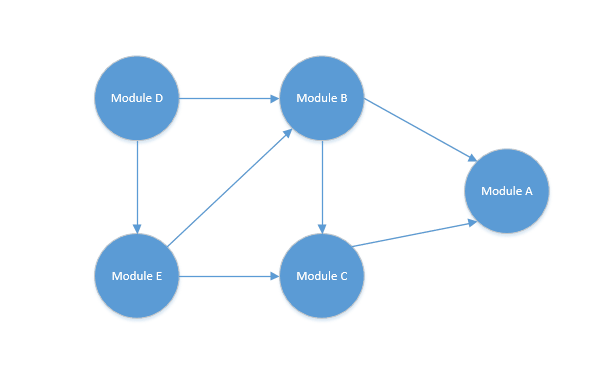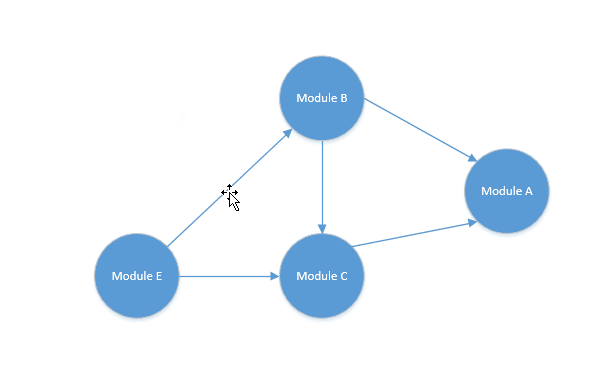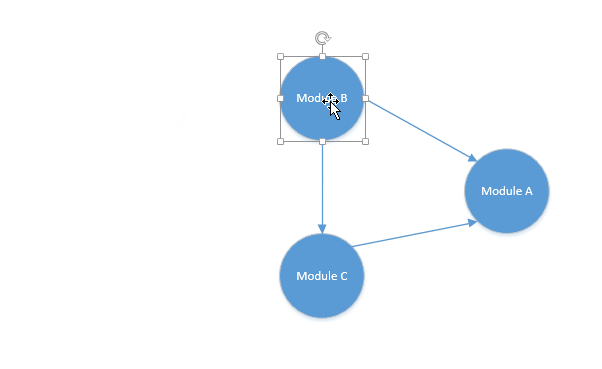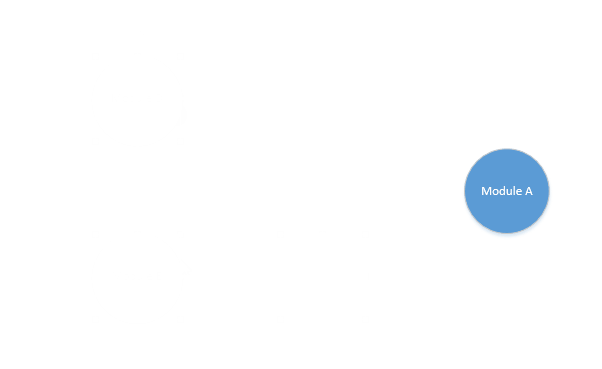
结果就是D->E->B->C->A 排完之后正好对应D依赖E和B,E依赖B和C,B依赖C和A,C依赖A
这个顺序在ABP的模块这看来是行不通的,需要在反转一次,最先加载A,才行。
C#实现深度优先搜索
有这样一个DAG图

如果对它进行排序的话,其实过程是这样的.
图中,顶点A是没有指向它的前驱的,所以从它开始访问
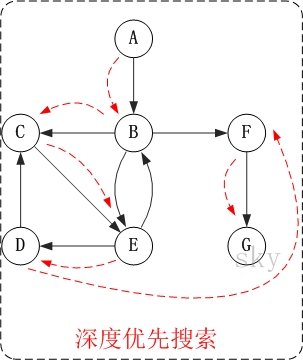
1.访问 A
2.访问 B
3.访问 C
在访问了 B 后应该是访问 B 的另外一个顶点,这里可以是随机的也可以是有序的,具体取决于你存储的序列顺序,这里先访问 C 。
4.访问 E
5.访问 D
这里访问 D 是因为 B 已经被访问过了,所以访问顶点 D 。
6.访问 F
因为顶点 C 已经被访问过,所以应该回溯访问顶点 B 的另一个有向边指向的顶点 F 。
7.访问 G
那么代码应该如何写呢?
source:需要排序的集合
getDepends:一个func委托,用于获取当前模块依赖的其他模块
方法内部维护了一个字典对象Visited 用于存储已经访问过的模块,key表示模块,value是一个bool,true时表示正在处理,false表示以及处理完成,
处理完成的模块会加入到sorted集合中
static List<T> MySort<T>(IEnumerable<T> source, Func<T, IEnumerable<T>> getDepends)
{
// 访问过的路径
Dictionary<T, bool> visited = new Dictionary<T, bool>();
// 已经排过序的
List<T> sorted = new List<T>();
foreach (var item in source)
{
Visit<T>(item, getDepends, visited, sorted);
}
return sorted;
}
static void Visit<T>(T item, Func<T, IEnumerable<T>> getDepends, Dictionary<T, bool> visited, List<T> sorted)
{
//已经访问过了
if (visited.ContainsKey(item))
{
bool isVisit = visited[item];
if (isVisit == true)
{
throw new Exception("循环引用");
}
}
//未访问
else
{
visited.Add(item, true);//true :正在访问 false:访问完成
//获取所有依赖
var depends = getDepends(item);
foreach (var depend in depends)
{
Visit(depend, getDepends, visited, sorted);
}
//访问完成
visited[item] = false;
sorted.Add(item);
}
}


