AGC019

质量果然挺高的。

贪心。

ll Q,H,S,D,N;
int main()
{
    cin>>Q>>H>>S>>D>>N;
    H=min(H,Q+Q);
    S=min(S,H+H);
    D=min(D,S+S);
    ll ans=N/2*D+(N&1)*S;
    cout<<ans<<"\n";
}

认真目测样例可以发现答案为不相等的字符对数+1。

char str[SZ]; int n;
int app[SZ];
int main()
{
    scanf("%s",str+1);
    n=strlen(str+1);
    for(int i=1;i<=n;++i)
        ++app[str[i]];
    ll tot=n*(ll)(n-1)/2;
    for(int i='a';i<='z';++i)
        tot-=(app[i]-1)*ll(app[i])/2;
    cout<<tot+1<<"\n";
}

首先答案大体上就是曼哈顿距离*100，为了几个喷泉绕路显然不优。

每一个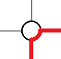可以使答案变小20-5pi，每个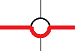会使答案变大10pi-20。

为了让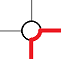尽量多，我们会经过尽量多的喷泉，这个可以直接按行排序之后把列LIS。

什么时候会有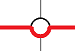呢？只有正好每行或者每列都怼了一个喷泉的时候。判一下就好了。

#define y1 yyy1
#define y2 yyy2
int x1,y1,x2,y2,n;
pii ps[SZ];
ld pi=acos(-1);
int bs[SZ];
void upd(int x,int y)
{
    for(;x<=n;x+=x&-x) bs[x]=max(bs[x],y);
}
int qmax(int x)
{
    int ans=-1e9;
    for(;x>=1;x-=x&-x) ans=max(ans,bs[x]);
    return ans;
}
#define yn yyn
int ys[SZ],yn=0;
int lis[SZ];
int main()
{
    memset(bs,-127/3,sizeof bs);
    scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&n);
    for(int i=1;i<=n;++i)
        scanf("%d%d",&ps[i].fi,&ps[i].se);
    if(x1>x2)
    {
        x1*=-1; x2*=-1;
        for(int i=1;i<=n;++i)
            ps[i].fi*=-1;
    }
    if(y1>y2)
    {
        y1*=-1; y2*=-1;
        for(int i=1;i<=n;++i)
            ps[i].se*=-1;
    }
    ps[++n]=pii(x1,y1);
    ps[++n]=pii(x2,y2);
    sort(ps+1,ps+1+n);
    for(int i=1;i<=n;++i)
        ys[++yn]=ps[i].se;
    sort(ys+1,ys+1+yn);
    int yy1=lower_bound(ys+1,ys+1+yn,y1)-ys;
    int yy2=lower_bound(ys+1,ys+1+yn,y2)-ys;
    for(int i=1;i<=n;++i)
        ps[i].se=lower_bound(ys+1,ys+1+yn,ps[i].se)-ys;
    int rr=0;
    for(int i=1;i<=n;++i)
    {
        lis[i]=qmax(ps[i].se)+1;
        if(ps[i]==pii(x1,yy1)) lis[i]=0;
        else if(ps[i]==pii(x2,yy2)) rr=lis[i]-1;
        upd(ps[i].se,lis[i]);
    }
    ld ans=(x2-x1)+(y2-y1);
    ans*=100.0;
    ans+=(pi-4)*5*rr;
    if(rr==min(x2-x1+1,y2-y1+1)&&rr)
        ans+=pi*5;
    printf("%.20lf\n",ans);
}

为了方便描述，我们记一个计数器t，往右+1，往左-1。那么当前a[i]对着的就是b[i+t]（模|A|意义下）。

假设我们枚举最后相等的时候的t=s，那么a[i]对着b[i+s]，我们就知道了哪些位需要flip一下。

考虑A在转的时候设计数器最小值为minn，最大值为maxn（minn<=0<=maxn）。要翻转A的某一位，可以往左转到第一个B为1的位置，也可以往右转到第一个B为1的位置，即有一个条件minn<=某个值或者 maxn>=某个值。

要取到某个minn和maxn、最后到达s，需要的最小翻的次数是多少呢？可以发现恰好是2(maxn-minn)-|s|。这个公式可以这么理解：如果s=0，那么显然要2(maxn-minn)，先移到maxn，再移到minn，再移回来或者先到minn再到maxn再回来。如果s>0，那么先到minn，再到maxn，然后只要移回到s，所以就是2(maxn-minn)-s。

假设s>=0，那么需要次数就是2(maxn-minn)-s，并且maxn>=s，minn<=0。设x=-minn，y=maxn-s，那么我们就是要最小化2(y+s+x)-s=2(x+y)+s，即最小化x+y，原来的条件就是x>=某个数 or y>=某个数。扫一下就好了。（从大到小枚举x，对不满足x的y需求取max）

如果s<0那就把A和B全翻过来。

char A[SZ],B[SZ]; int n,ans;
int mi[SZ],ma[SZ],mx[SZ];
void work()
{
    for(int i=0;i<n;++i)
    {
        mi[i]=ma[i]=0;
        while(B[(i+ma[i])%n]!='1') ++ma[i];
        while(B[(i+mi[i]+n)%n]!='1') --mi[i];
    }
    for(int s=0;s<n;++s)
    {
        for(int r=0;r<n;++r) mx[r]=0;
        int dif=0;
        for(int r=0;r<n;++r) if(A[r]!=B[(r+s)%n])
            mx[-mi[r]]=max(mx[-mi[r]],ma[r]-s),++dif;
        int ly=0,ca=1e9;
        for(int r=n-1;r>=0;--r)
            ca=min(ca,ly+r), ly=max(ly,mx[r]);
        ans=min(ans,2*ca+s+dif);
    }
}
int main()
{
    scanf("%s%s",A,B);
    n=strlen(A); ans=1e9;
    bool ha=0,hb=0;
    for(int i=0;i<n;++i)
        if(A[i]=='1')ha=1;
    for(int i=0;i<n;++i)
        if(B[i]=='1')hb=1;
    if(!hb)
    {
        if(ha) puts("-1");
        else puts("0");
        return 0;
    }
    work(); reverse(A,A+n);
    reverse(B,B+n); work();
    printf("%d\n",ans);
}

这里讲一下 http://codeforces.com/blog/entry/54027?#comment-381549 这个做法。

考虑swap有几种：

A 10 10 11 11

B 01 11 11 01

其中

交换完之后第一列的10就固定了，直接就GG了。

首先我们可以注意到01和10的列数是一样的（否则A和B里1的个数就不同了）。

我们先考虑11 11这种情况，贡献A的一方只能是11，因为如果是01换过来一个1，那么A已经换过了，贡献B的一方可以是换过来一个1的01（而且01合法的只能是换过来一个1）（注意这里贡献A和B的可以是同一个）。

因为11 11换了也是白换，所以我们可以先把这部分的方案数计算一下。

假设有x个列为01，y个列为11，设有y-i个11 11这种情况，那么贡献A的可以是y个中任一，贡献B的可以是x+y中任一，所以只要把另外两种情况的方案数乘上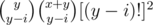就好。

接下来我们只有

10 和 10 这两种情况了。

01 11

此时，设g[x][i]为有x个列为01，x个列为10，i个列为11的方案数，那么g[x][i]=x^2g[x-1][i]（10和01匹配）+xig[x][i-1]（11和01匹配）

通过换元这个式子还可以进一步化简，不是重点这里就不说了，可以参看上面那个链接。

char A[SZ],B[SZ];
int n;
ll f[10009];
#define MOD 998244353
ll fac[SZ],rfac[SZ];
ll qp(ll a,ll b)
{
    ll x=1;
    while(b)
    {
        if(b&1) x=x*a%MOD;
        a=a*a%MOD; b>>=1;
    }
    return x;
}
int main()
{
    fac[0]=1;
    for(int i=1;i<SZ;++i)
        fac[i]=fac[i-1]*i%MOD;
    rfac[SZ-1]=qp(fac[SZ-1],MOD-2);
    for(int i=SZ-1;i>=1;--i)
        rfac[i-1]=rfac[i]*i%MOD;
    scanf("%s%s",A+1,B+1); n=strlen(A+1);
    int x=0,y=0;
    for(int i=1;i<=n;++i) if(A[i]=='1')
        (B[i]=='0')?(++x):(++y);
    f[0]=1;
    for(int i=1;i<=x;++i)
        for(int j=1;j<=y;++j)
            f[j]=(f[j]+i*f[j-1])%MOD;
    ll ans=0;
    for(int j=0;j<=y;++j)
        ans=(ans+f[j]*rfac[x+j])%MOD;
    ans=ans*fac[x]%MOD*fac[x]%MOD
    *fac[y]%MOD*fac[x+y]%MOD;
    ans=(ans%MOD+MOD)%MOD;
    printf("%d\n",int(ans));
}

多项式做法可以参见 http://blog.csdn.net/wxh010910/article/details/77622473

因为每次回答后都告诉了你正误，所以最优策略一定是答剩的比较多的一个，答对概率就是剩的多的个数 / 总个数。

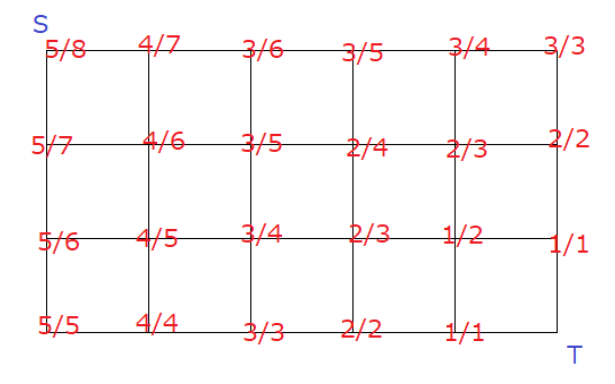
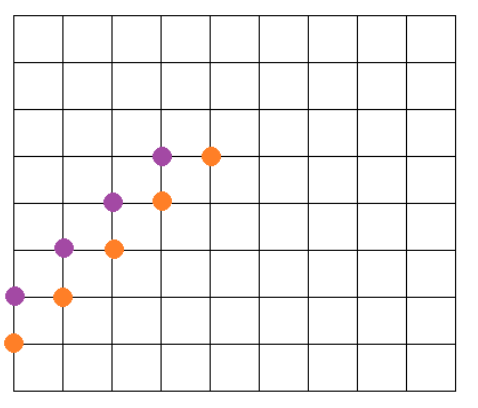
考虑把回答的过程画成图中这样，每个点上标上之前说的剩的多的个数/总个数，那么问的就是这个网格图中往右往下走从S到T的期望路径长度。

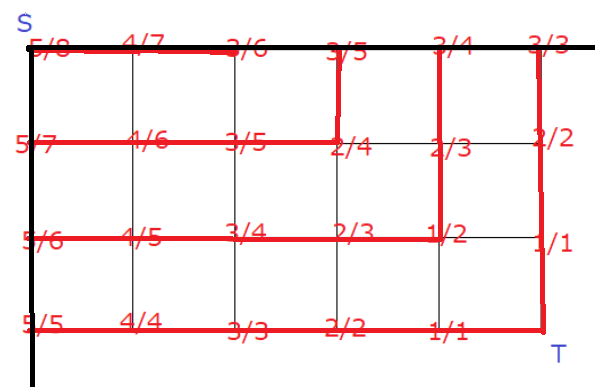
考虑把分子不一样的格线标成实线，那么图一定形如这样

主要的思路是从T开始一条一条对角线往上枚举。一条路径显然恰过每条对角线的一个点。

考虑一条路径在当前这条对角线的交点的分子，如果我们知道了每个分子的和，那么ans+=分子/公分母/路径数即可。

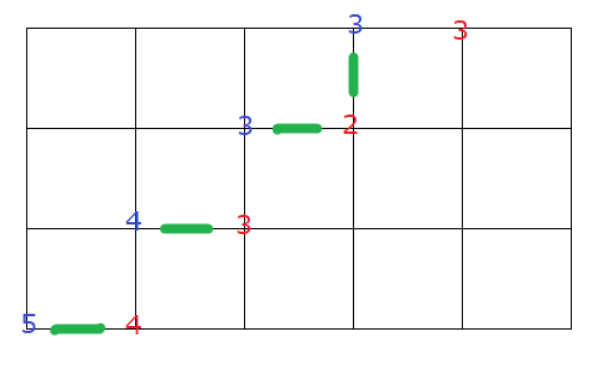
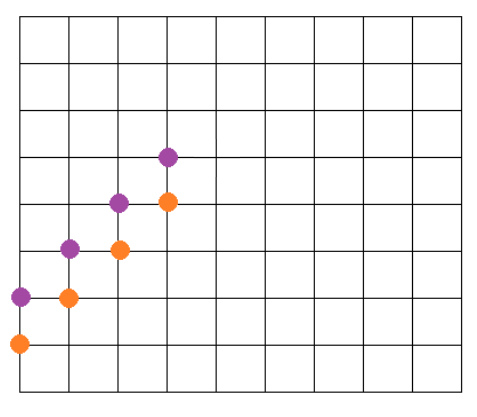
如下图考虑一条分子为5433的对角线，上一条对角线分子为4323。

考虑一条路径经过上一条对角线之后经过这一条对角线，分子只能+1或者不变，如果经过实线的话就会+1，否则不变。

那么现在我们的任务就变成了统计经过这些实线的路径条数。

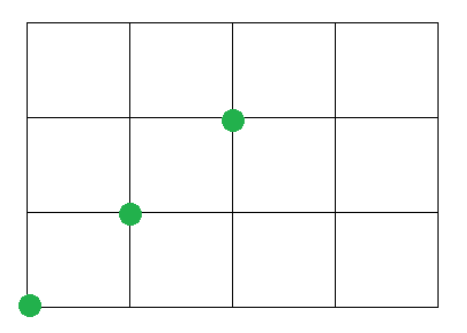
如上图，我们先考虑横着的实线，计数线不太好，我们考虑把格子往左压扁一格：

显然原来经过实线对应现在经过绿点。

这个计数仍然不好计，考虑还是利用递推，假设我们知道了上一条对角线经过这些点的方案数如何推出下一条的？

有两种基本情况：

假设我们知道了经过橙点的方案数。

这种情况下考虑经过紫点的路径一定也经过橙点，而经过橙点的路径，不经过紫点的只有经过最右边那个橙点，并且没经过最右边的紫点的路径，方案数即从(S到这个橙点路径数-S到最右边紫点路径数)*这个橙点到T的路径数。

这种情况类似，经过紫点而不经过橙点的路径数只有 S到最右边紫点路径数*(最右边紫点到T路径数-最右边橙点到T路径数)。

需要注意的是实际上是哪种情况并不是由点数决定的，而是由最右边的紫点和橙点的位置关系决定的。

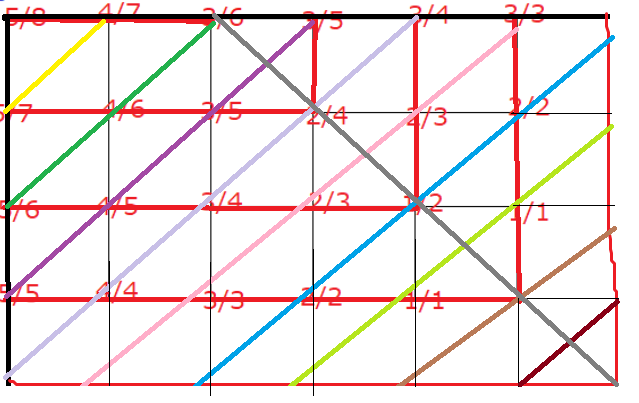
如何方便地求出某两条对角线间最右边的一段实线呢？如图（瞎画的，不要在意细节）：

把对角线和灰线求交点，上/下取整即为最右边的实线位置。

#define SZ 1234567
int n,m;
const int MOD=998244353;
ll fac[SZ],rfac[SZ];
ll qp(ll a,ll b)
{
    ll x=1;
    while(b)
    {
        if(b&1) x=x*a%MOD;
        a=a*a%MOD; b>>=1;
    }
    return x;
}
inline ll rt(int a,int b)
{
    return fac[a+b]*rfac[a]%MOD*rfac[b]%MOD;
}
int main()
{
    fac[0]=1;
    for(int i=1;i<SZ;++i) fac[i]=fac[i-1]*i%MOD;
    rfac[SZ-1]=qp(fac[SZ-1],MOD-2);
    for(int i=SZ-1;i>=1;--i)
        rfac[i-1]=rfac[i]*i%MOD;
    cin>>n>>m;
    if(n>m) swap(n,m);
    //灰线为y=x+m-n
    int px1,py1,px2,py2; ll cv1,cv2,cv=0,ans=0;
    //考虑对角线x+y=g和x+y=g+1的关系 
    for(int g=m+n-1;g>=0;--g)
    {
        {
        int r=max(g+n-m+1,0),y,u=min(g,n);
        if(r&1) y=(r+1)/2;
        else y=r/2;
        int a=y,b=g-y;
        if(y==u) cv1=rt(y,g-y)*rt(n-y,m-1-(g-y))%MOD;
        else if(px1==a)
            cv1-=(rt(px1,py1)-rt(a,b))*rt(n-px1,m-1-py1)%MOD;
        else
            cv1+=rt(a,b)*(rt(n-a,m-1-b)-rt(n-px1,m-1-py1))%MOD;
        px1=a; py1=b; cv1%=MOD;
        }
        {
        int r=g+n-m+1,y,d=max(g-m,0);
        if(r&1) y=(r-1)/2;
        else y=r/2; --y;
        if(d>y) cv2=0;
        else
        {
        int a=y,b=g-y;
        if(y==d) cv2=rt(y,g-y)*rt(n-1-y,m-(g-y))%MOD;
        else if(px2!=a)
            cv2-=(rt(px2,py2)-rt(a,b))*rt(n-1-px2,m-py2)%MOD;
        else
            cv2+=rt(a,b)*(rt(n-1-a,m-b)-rt(n-1-px2,m-py2))%MOD;
        px2=a; py2=b; cv2%=MOD;
        }
        }
        cv+=cv1+cv2; cv%=MOD;
        ans+=cv*qp(m+n-g,MOD-2)%MOD;
    }
    ans=ans%MOD*qp(rt(n,m),MOD-2)%MOD;
    ans=(ans%MOD+MOD)%MOD;
    printf("%d\n",int(ans));
}

UPD：wxh吊打tourist http://blog.csdn.net/wxh010910/article/details/77752687

考虑答案变得不那么套路的时候，就是经过灰线的时候，直接算就好了

posted @ 2017-08-29 10:54 fjzzq2002 阅读(1600) 评论(0) 编辑收藏举报

刷新页面返回顶部

AGC019

公告