NEERC=Not Easy European Regional Contest
据说NEERC天天被搬，赶紧做了好了。在Claris和Google的帮助下做了10题，感谢cls。
http://codeforces.com/gym/100851
需要注意的是在cf上面做的时候标明文件名的题要开freopen（没标的那题是交互）。
这套题很好，所以希望想要认真想想的同学还是别手贱点开题解了，下面的顺序按通过人数降序。
A
给一个n*n的矩阵，开始(x,y)的格子上填的是x+y。
有两种询问（操作），第一种是输出一行的和并把这行清零，第二种是输出一列的和并把这列清零。
询问个数为q。n<=1e6，q<=1e5。
题解
如果没有清空直接等差数列求和。
如果一行或一列询问两次清空后显然没用。
否则对于某个行求和，影响它的只是之前的列清空，把清空的列号和记下来即可。
E
有n位老司机要出题，第i位老司机想了p[i]道简单题，每道难度在[0,49]。每位老司机都经验丰富，他们每人都有无限道难度为50的难题。他们要选k道题出成NEERC。
他们是这样出题的，第一位老司机从自己的简单题列表选出第一道，如果简单题用完了就选出一道难题，如果这道题的难度不小于之前所有选出的题难度之和，那么就选出这题，接下来换第二位老司机，第三位老司机...第n位老司机选完后又轮到第一位老司机。如果已经没有题可以选了（没有题满足这道题的难度不小于之前所有选出的题难度之和），那么剩下就啥都不管全选难题。选完k道题就结束。
问选出的题难度值之和。数据范围很小。
题解
G
给n个正常的线性同余随机数生成器：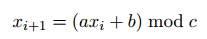
，求n个随机数生成器生成出的任意n个数之和中，不被k整除的最大可能值。如果不存在就输出-1。n<=10000，k<=1e9，c[i]<=1000。
题解
先求出每个随机数生成器可以求出哪些数。
首先如果每个随机数生成器生成出的最大值不被k整除那么就稳了。
否则我们只要对于每个随机数生成器，再找到不和最大值mod k同余的最大的就好。
F
有一只蛤要过河，河长这样：
他开始在x=0，要跳到x=w，河上有若干石头，他要最小化自己每一步跳过的距离的最大值。
因为蛤有神力，它可以放下一块石头，使这个值变小，输出任何一个可以最小化这个值的放石子位置，保留三位小数。
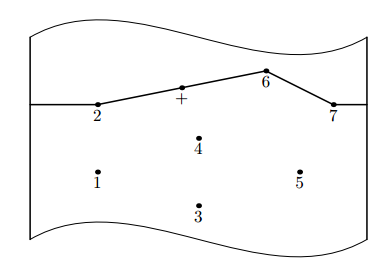
坐标1e9，石子数量<=1000。
题解
如果不能多放石子，那么就是从S到T的一个简单的min值最短路，使用prim（或者叫做dijkstra也行，反正就是同一个东西）即可。不要用堆优化啥的，图是稠密的，直接用平方暴力就好。
现在可以多放石子，那么就建分层图，第一层是没放石子的，第二层是放石子的，跨过层的中间放一个石子，可以使距离减半。注意边界情况。
J
曾经有一个善良的交互库，交互库中藏了一个n位的01串，n是一个偶数。你只知道n，你每次可以输入一个n位01串，交互库会告诉你有几位与隐藏串相同，你需要还原出隐藏串。
邪恶的出题人改动了这个交互库，现在你每输入一个n位01串，设与隐藏串相同位数为p，如果p=n/2或p=n，那么交互库会输出p，否则交互库只会输出0。
现在你仍然需要还原隐藏串，当交互库输出n时你就还原成功了。你的询问次数必须不超过n+500。n<=1000。
题解
首先我们先要想办法让交互库输出点信息，比如输出n/2。
我们来随机一个01串！每位匹配的概率都是1/2，所以有很大概率搞出一个n/2！
讲道理：“很大”概率为C(n,n/2)/2^n，n=1000时约为0.025225，虽然看起来好像不大，但是400次还没有随到的概率为(1-0.025225)^400约等于0.0036%，如果没有随出来应该是时候买张彩票了。
有了这样一个匹配n/2位的串，我们可以这么做：从前往后考虑相邻两位，把它们都取反，如果仍然n/2个匹配，那么必然是一位正确另一位不正确，否则两位正确与否相同。那么经过n-1次我们已经知道了每相邻两位匹配状态相同或不同了，我们只要再枚举两次第一位匹配还是不匹配就可以还原出来了。
L
你正在玩一个建造金字塔的2d游戏，开始一条线上宽度为w的一排，每格叠了若干石块，没有悬空的。
现在你可以放一些石块，但是有限制，你在一个格子上能放石块，当且仅当它的下面三格（左下方、下方、右下方这三格）都已经有石块了。直接在地上放也不行。
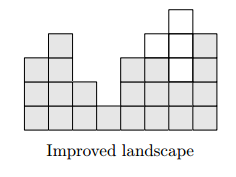
你现在最多能放n块石块，想要叠的尽量高（使最高的一块高度尽量高），输出最高高度。
开始的石块堆数w<=1e5，n<=1e18，开始每格高度[1,1e9]。
题解
我们先枚举要把哪块堆成最高点，考虑堆高怎么堆，最后肯定是堆成金字塔状的一个形状。
类似这样，由于不能堆到地上，所以这个形状肯定左边和右边都得有东西挡住。
反正就是左边和右边都得有一列至少不低于这个形状，然后只有没有挡住的中间这些要计入答案。
比如中间一列为x，高度为a[x]，那么左边的某一列l，需要的高度就为a[x]-(x-l)=a[x]-x+l，如果它没有被挡住，那么就需要付出a[x]-x+l-a[l]个石子，被挡住的充要条件也就是a[x]-x<=a[l]-l。
对于左边我们只要二分一下到哪里被挡住了，查一下a[l]-l的最大值比较一下，把中间的a[x]-x+l-a[l]计入要用的石子数即可。右边同理。
知道堆到每个高度需要的石子个数，只要二分一下就好了。
这样是两个log的（如果你用O(1)rmq），通过一些技巧可以去掉一个log。
网上好像有一种更加科学的做法，参见 http://blog.csdn.net/u010568270/article/details/52382293。
K
给一个有向图，问有没有哈密顿回路（经过每个点恰好一次、不重复经过一条边），有的话输出任意一个以1开始和结束的哈密顿回路顶点序列。
顶点数<=1e5，边数<=顶点数+20。
题解（感谢Claris）
先考虑给每个点指定一个出边。
如果每个点指定了一个出边，如何判断是否合法？我们首先得确保边的另一端点也是一个排列，这个只要记每个点被作为另一端几次，没有一个点被作为两次就好了。接下来我们已经确定了这是一个置换，那么我们只要确保所有点连上出边只有一个联通块即可。
考虑原问题。如果有一个点没出边显然无解。考虑边数<=顶点数+20，大部分点都只会有一条出边，只会有至多20个点有多条出边。
暴搜这些点的出边，按照上面的做法判断即可。每个点被作为另一端几次开个数组，所有点连上出边只有一个联通块只要用正常的按秩合并并查集就好了。
B
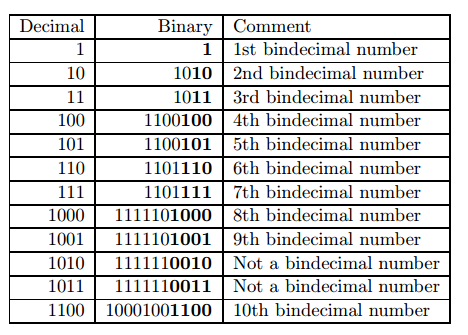
定义一个数x是bindecimal的当且仅当这个数转成二进制后，这个数的十进制表示是这个01串的后缀。
求从小到大第n个bindecimal数，n<=10000。
题解（不会，Google的）
我们定义一个数为k-bindecimal数当且仅当这个数<10^k并且10进制下最后k位与2进制下最后k位相同（不够则补0）。
首先注意到10^n=2^n*5^n，那么10^n肯定是(n+1)-bindecimal数。
考虑(k+1)-bindecimal数和k-decimal数之间的关系，一个(k+1)-bindecimal数如果第10^k这一位是0，那么它就是k-bindecimal数的一个子集（k-bindecimal数中2^k一位为0的），否则由于10^k本身就是(k+1)-bindecimal的，那么去掉这一位还是k-bindecimal数2^k一位为0的这一子集。
所以我们只要从小到大枚举每个k，每次把k-bindecimal数集中2^k一位为0的每个数加入(k+1)-bindecimal数集，加上10^k之后再加入(k+1)-bindecimal数集，这样就可以生成每个k-bindecimal数集。当然k-bindecimal数集中的数不一定全部合法，只有10^k这一位不是0的才是真的bindecimal数。
经过测试k<=180的k-bindecimal数集中真的bindecimal数大约就有1.5w个了，排序后输出即可。
由于这些数比较大，建议使用比较科学的语言，例如python。当然如果是acm现场就只能java保平安了。
C
定义仙人掌为没有自环、重边的无向连通图，其中每条边至多在一个简单环上。
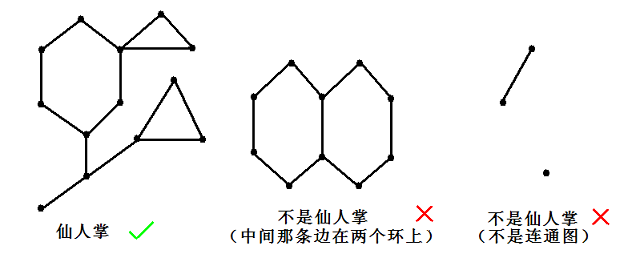
现在给你一棵仙人掌，问有多少种方案删去一条边再加上一条不同的（连接顶点不同的）边使得产生的图仍为仙人掌，删去或加入的边不同就算不同方案。顶点数<=50000，采用neerc特色仙人掌读入方式（读入参见bzoj1023）。
题解
仙人掌？考虑圆方树dfs树。
我们对仙人掌进行dfs，那么得到了一棵dfs树，现在仙人掌上有两种边，一种叫树边，一种叫非树边。
对于一条非树边，它会cover树上这条边两个端点间的路径，由于一条边只在一个简单环上，那么一条边只会被cover一次。
那么现在仙人掌上有三种边了，一种是没被cover的树边，一种是被cover的树边，一种是非树边。
考虑删除哪一种边，如果删除的是没被cover的树边，那么这条边去掉之后把仙人掌割开了，加入的边就需要把仙人掌重新连上，所以方案数就是分开之后两个联通块点数之积。
对于另两种情况，先假设没有删边直接添一条边，那么我们可以把没被cover的树边全部连上，新的边只能在每个这样的树块里面连。
如果删除的是被cover的树边或者是非树边，那么这一整个环都由被cover树边变成了没被cover的树边。反正删哪条边都一样，只要拿个按秩合并并查集大力连上然后算方案数就好。
需要注意不能连重边和删加同一条边，不过样例过了应该就没啥事了。
D
给一个多边形和一种三角剖分，按这个连边，边权为1，多次询问顶点间最短路。
顶点数<=50000，询问数<=1e5。
题解（Google的）
考虑分治。每次找一条分得尽量均匀的对角线把多边形裁成两半，然后两半继续分治，分治到三角形结束。
可以证明每次最坏只会分成1:2这样的（不会证，题解这么写的），所以分治只会有log层。
分治的时候从这条对角线的两个顶点开始bfs，因为跨过对角线的两个点最短路一定要经过对角线，所以只要对经过两端点的最短路取个min就好。
把分治树建出来求个lca，那么只要找到lca那层分治的最短路求答案就好了。
还有一道奇怪的计算几何和一道奇怪的大模拟，所以大概也不会再做了。完结撒花！
，求n个随机数生成器生成出的任意n个数之和中，不被k整除的最大可能值。如果不存在就输出-1。n<=10000，k<=1e9，c[i]<=1000。
