Weekly Traning Farm 16
先安利一下这套比赛,大概是doreamon搞的,每周五晚上有一场,虽然没人做题目质量挺高的 http://codeforces.com/group/gRkn7bDfsN/contests(报名前要先报名group,不用审核) 每一次的题解可以在这里看到 http://dreamoon4.blogspot.tw/(梯子自备)
这场是http://codeforces.com/group/gRkn7bDfsN/contest/210418
这一场是类似之前某一场cf把每题拆成几个数据规模的题目分别给分。之前连续出了两三场乱七八糟的构造题
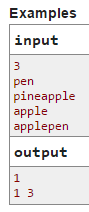
A Apple Pen
给出n个字符串和一个母串,问这个母串能用多少种方式从n个字符串中选2个拼成并输出方案(可以假装方案不是很多)。2<=n<=10^6,字符串总长<=2e7,母串长度<=1e6。
喜闻乐见的样例。
这个题十分菜啊,假装每个字符串分别为前缀或者后缀判断是否可行,然后合在一起输出。之前脑子里进水了想了一堆奥妙重重的做法
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first #define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);} #define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);} #define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);} #define es(x,e) (int e=fst[x];e;e=nxt[e]) #define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e]) #define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");} #define VIZ2 {printf("graph G{\n"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;\n",i,vb[e]); puts("}");} #define SZ 1234567 int n; string s[1000007]; string t; char tmp[20000007]; vector<int> vs[1234567],vs2[1234567]; vector<pii> rst; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%s",tmp); s[i]=tmp; } scanf("%s",tmp); t=tmp; for(int i=1;i<=n;i++) { if(s[i].length()>t.length()) continue; if(t.substr(0,s[i].length())==s[i]) vs[s[i].length()].pb(i); if(t.substr(t.length()-s[i].length(),s[i].length())==s[i]) vs2[t.length()-s[i].length()].pb(i); } for(int i=0;i<t.length();i++) { for(auto a:vs[i]) { for(auto b:vs2[i]) { if(a==b) continue; rst.pb(pii(min(a,b),max(a,b))); } } } sort(rst.begin(),rst.end()); rst.erase(unique(rst.begin(),rst.end()),rst.end()); printf("%d\n",rst.size()); for(int i=0;i<rst.size();i++) printf("%d %d\n",rst[i].fi,rst[i].se); }
B Two Swords
有n把剑,有20种属性,每把可能会有或无每种属性,询问q次,每次要求找出两把剑,每种要求的属性至少要有一把剑具有,问找出这两把剑的方案数。n,q<=50W。
大概是个fwt/集合幂级数的裸题。
首先我们先把每种属性是否具有当做一个二进制数,拿个数组存下来每个二进制数出现的次数,就叫数组x好了。
那我们第一步就是要求
for(int i=0;i<(1<<20);i++) for(int j=0;j<(1<<20);j++) a[i|j]+=x[i]*x[j];
从fwt的角度理解:这就是个or的fwt,直接用fwt水~ http://picks.logdown.com/posts/179290-fast-walsh-hadamard-transform(我当时比赛时就是这么想的...)
从集合幂级数的角度理解:这就是个集合并卷积,我们可以用经典的快速莫比乌斯变换+快速莫比乌斯反演来做。(似乎ysy和出题人都是这么想的)
其实这两个做法只是同一个东西的两种写法...
这个数组求出来之后我们可以求出或恰好为一个数的方案数,但是题目中询问对不要求的属性不作要求,然后我们可以把每一位反过来,再用一发快速莫比乌斯变换。
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first #define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);} #define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);} #define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);} #define es(x,e) (int e=fst[x];e;e=nxt[e]) #define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e]) #define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");} #define VIZ2 {printf("graph G{\n"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;\n",i,vb[e]); puts("}");} #define SZ 666666 int mx=(1<<20); int n,q; ll cnt[2333333],qwq[2333333],inv[2333333]; char s[233]; int toi(char* s) { int x=0; for(int i=0;s[i];i++) x=x*2+s[i]-48; return x; } void trans(ll* g,int k) { for(int i=0;i<20;i++) { int all=(mx-1)^(1<<i); for(int s=0;s<mx;s++) { if((s&all)!=s) continue; g[s^(1<<i)]+=g[s]*k; } } } int main() { scanf("%d%d",&n,&q); for(int i=1;i<=n;i++) { scanf("%s",s); ++cnt[toi(s)]; } for(int i=0;i<mx;i++) qwq[i]=cnt[i]; trans(cnt,1); for(int i=0;i<mx;i++) cnt[i]*=cnt[i]; trans(cnt,-1); for(int i=0;i<mx;i++) inv[(mx-1)^i]=(cnt[i]-qwq[i])/2; trans(inv,1); while(q--) { scanf("%s",s); int x=toi(s); printf("%I64d\n",inv[(mx-1)^x]); } }
代码十分简洁明了。当然你可以把trans换成分治fwt效果是一样的= =
C Zekken
有一条数轴,你开始在0的位置,每单位时间你至多能移动d个单位,在ti时刻xi位置会出现一个宝物,然后马上消失,只有ti时刻你站在xi位置才能捡到。问最多你能捡到几个宝物。宝物数量n<=50W,没有ti、xi都相等的宝物。
先说结论,把一个点换成(ti*d-xi,ti*d+xi),如果有任一维<0就忽略这个点,否则将一维排序另一维lis即为答案。
我们先考虑d=1的情况,对于d≠1的显然只要把一秒续成d秒就行了(即ti*=d)。
我们考虑把(xi,ti)当做一个点,显然下一个点只能在左右45°内
我们往右转45°就变成了要在这个点的右上方,(a,b)右转45°就成了((a+b)/sqrt(2),(b-a)/sqrt(2)),我们忽略那个sqrt(2),(xi,ti)转完就相当于(xi+ti,ti-xi)。
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first #define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);} #define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);} #define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);} #define es(x,e) (int e=fst[x];e;e=nxt[e]) #define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e]) #define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");} #define VIZ2 {printf("graph G{\n"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;\n",i,vb[e]); puts("}");} #define SZ 666666 typedef pair<ll,ll> pll; int n,d,x[SZ],t[SZ],bs[SZ],dp[SZ]; ll gg[SZ],tmp[SZ]; pll ps[SZ]; int mx(int g) { int ans=0; for(;g>=1;g-=g&-g) ans=max(ans,bs[g]); return ans; } void edt(int x,int y) { for(;x<=n;x+=x&-x) bs[x]=max(bs[x],y); } int main() { scanf("%d%d",&n,&d); for(int i=1;i<=n;i++) { scanf("%d%d",x+i,t+i); ps[i]=pll(t[i]*(ll)d-x[i],t[i]*(ll)d+x[i]); if(ps[i].fi<0||ps[i].se<0) { --i; --n; continue; } } sort(ps+1,ps+1+n); for(int i=1;i<=n;i++) gg[i]=ps[i].se; for(int i=1;i<=n;i++) tmp[i]=gg[i]; sort(tmp+1,tmp+1+n); int ans=0; for(int i=1;i<=n;i++) { gg[i]=(lower_bound(tmp+1,tmp+1+n,gg[i])-tmp); dp[i]=mx(gg[i])+1; edt(gg[i],dp[i]); ans=max(ans,dp[i]); } printf("%d\n",ans); }