圆方树学习
圆方树是一种数据结构。
这个东西原始的出处应该是paper
《Maintaining bridge-connected and biconnected components on-line》
tarjan和另外一个人写的...当时叫forest data structure
然后这个东西似乎已经流行很久了?http://blog.csdn.net/PoPoQQQ/article/details/49513819
cjk大爷最近发了一篇博客写这个:http://immortalco.blog.uoj.ac/blog/1955
这篇里的例题啊啥的都是cjk大爷的
首先圆方树是用来解决静态仙人掌问题的。
(这里的静态仙人掌是说仙人掌不会活动,没有link啊,cut啊啥的)
仙人掌是啥大家都知道吧...
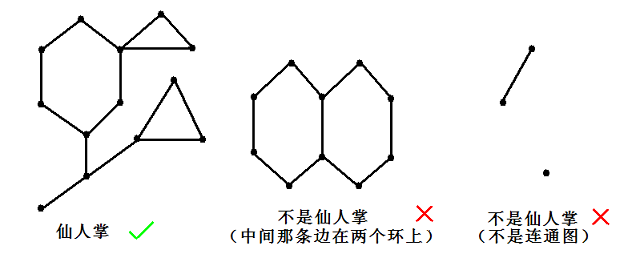
比如开始有一个这样的仙人掌:
可以发现这张图上有两个环,哪两个就不说了。
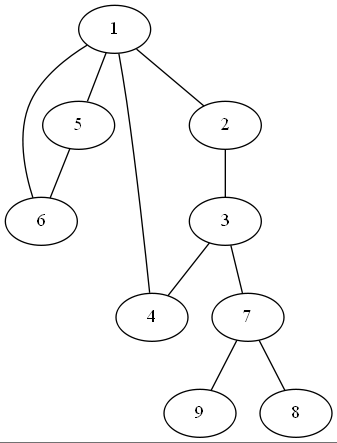
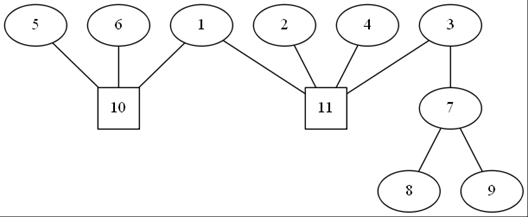
我们把图上的每个环单独当做一个点,我们叫这些新点方点,原来的点叫原点,然后把原来的环连成一个菊花,我们就有了一棵美观的圆方树!
啊圆方树就是这么简单的一个东西。
首先怎么建这个圆方树?
我们在仙人掌上面跑tarjan,我们考虑x的一条出边x->b(出边就是说x比b先访问到),那么如果dfn[x]<=low[b],我们发现我们找到了一个环。
(需要注意的是,这里的环可能只是一条边,要特判掉)
此时我们维护一个栈,一直弹栈,弹到b停下,加上x就组成了一个环。此时我们把x叫做这个环的根。
此时我们可以发现弹栈的顺序正好组成了环一圈的顺序,并且正好是倒着的dfs序。
那我们倒过来(当然不倒你舒服也行),就可以二分找一个点在环上什么位置了。
(当然如果你追求常数,你可以先判一下这个点是不是环根,否则每个点只会在一个环里就可以记下来,不过感觉不是很优美就没写)
然后我们可以把这些东西拿一坨vector存下来...圆方树就建好啦~
由于比较弱只写了前面的几题...还是比较好写的...
A. bzoj2125
给出一棵仙人掌,q次询问两点最短路径。
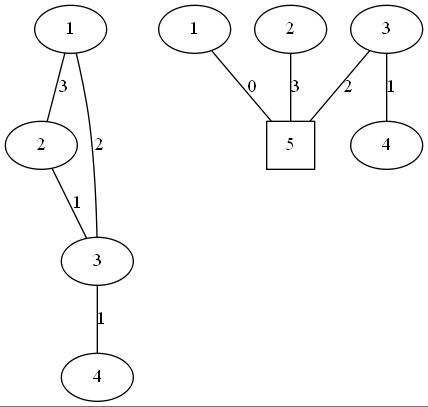
现在我们这个圆方树上可以加边权啦!如果一条边是圆圆边,那么就是原来的边权,如果是圆方边,那么边权等于环的根到那个圆点的最短路径长度。
现在我们要询问两个点的最短路,我们查一下lca,如果是圆点,那么这个最短路就是树上的长度。如果是方点,我们倍增跳到这个环上,在每个环上记一下前缀和,判一下走哪一侧就行了。
感人至深的代码
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first #define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);} #define es(x,e) (int e=fst[x];e;e=nxt[e]) #define SZ 666666 //don't pass directly in arguments! struct G { int n,M,fst[SZ],vb[SZ],vc[SZ],nxt[SZ]; G() {M=0; n=0;} void ad_de(int a,int b,int c) { ++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b; vc[M]=c; } void adde(int a,int b,int c) { ad_de(a,b,c); ad_de(b,a,c); } }; //CST=Circle-Square-Tree namespace cst { G* s; //source int M,n,fst[SZ],vb[SZ],nxt[SZ],vc[SZ]; void ad_de(int a,int b,int c) { ++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b; vc[M]=c; } void adde(int a,int b,int c) { ad_de(a,b,c); ad_de(b,a,c); } int ss[SZ],sn=0,C=0,dfn[SZ],low[SZ],fe[SZ]; int cl[SZ],rot[SZ],tag[SZ]; vector<int> hs[SZ],ls[SZ]; vector<ll> qzl[SZ]; void tarjan(int x) { dfn[x]=low[x]=++C; ss[++sn]=x; for(int e=s->fst[x];e;e=s->nxt[e]) { int b=s->vb[e]; if(dfn[b]) {low[x]=min(low[x],dfn[b]); continue;} fe[b]=s->vc[e]; tarjan(b); low[x]=min(low[x],low[b]); if(dfn[x]<=low[b]) { if(ss[sn]==b) {adde(x,b,s->vc[e]); --sn; continue;} int g=++n,tl=0; rot[g]=x; int fl=ss[sn]; tag[fl]=g; while(1) { int cur=ss[sn--]; hs[g].push_back(cur); ls[g].push_back(fe[cur]); tl+=fe[cur]; if(cur==b) break; } hs[g].push_back(x); ls[g].push_back(-1); cl[g]=tl; } } for(int e=s->fst[x];e;e=s->nxt[e]) { int b=s->vb[e]; if(!tag[b]) continue; int r=tag[b]; cl[r]+=s->vc[e]; ls[r][ls[r].size()-1]=s->vc[e]; tag[b]=0; } } #define S 20 ll dc[SZ]; int fa[SZ],p[SZ][S],sz[SZ],dep[SZ]; void dfs(int x,int f=0) { sz[x]=1; for es(x,e) { int b=vb[e]; if(b==f) continue; fa[b]=p[b][0]=x; dep[b]=dep[x]+1; dc[b]=dc[x]+vc[e]; dfs(b,x); sz[x]+=sz[b]; } } int jump(int x,int d) { for(int s=S-1;s>=0;s--) { if(p[x][s]&&dep[p[x][s]]>=d) x=p[x][s]; } if(dep[x]!=d) exit(-1); return x; } int lca(int a,int b) { if(dep[a]>dep[b]) swap(a,b); b=jump(b,dep[a]); if(a==b) return a; for(int s=S-1;s>=0;s--) { if(p[a][s]!=p[b][s]) a=p[a][s], b=p[b][s]; } return p[a][0]; } void pre() { n=s->n; M=0; for(int i=1;i<=s->n;i++) if(!dfn[i]) tarjan(i); for(int i=s->n+1;i<=n;i++) reverse(hs[i].begin(),hs[i].end()), reverse(ls[i].begin(),ls[i].end()); //now same circle is at dfn-order for(int i=s->n+1;i<=n;i++) { ll len=-ls[i][0]; for(int j=0;j<hs[i].size();j++) { len+=ls[i][j]; qzl[i].push_back(len); adde(i,hs[i][j],min(len,cl[i]-len)); } } for(int i=1;i<=n;i++) if(!fa[i]) dfs(i); for(int i=1;i<S;i++) { for(int j=1;j<=n;j++) p[j][i]=p[p[j][i-1]][i-1]; } } int fpos(int p,int x) { vector<int> &h=hs[p]; int l=0,r=h.size()-1; while(l<r) { int mid=(l+r)>>1; if(dfn[h[mid]]>=dfn[x]) r=mid; else l=mid+1; } return l; } ll query(int a,int b) { int lc=lca(a,b); if(lc<=s->n) return dc[a]+dc[b]-dc[lc]*2; int pa=jump(a,dep[lc]+1),pb=jump(b,dep[lc]+1); ll ans=dc[a]-dc[pa]+dc[b]-dc[pb]; int ppa=fpos(lc,pa),ppb=fpos(lc,pb); ll hl=qzl[lc][max(ppa,ppb)]-qzl[lc][min(ppa,ppb)]; hl=min(hl,cl[lc]-hl); return ans+hl; } } #define gc getchar() int g_i() { int tmp=0; bool fu=0; char s; while(s=gc,s!='-'&&(s<'0'||s>'9')) ; if(s=='-') fu=1; else tmp=s-'0'; while(s=gc,s>='0'&&s<='9') tmp=tmp*10+s-'0'; if(fu) return -tmp; else return tmp; } #define gi g_i() #define pob #define pc(x) putchar(x) namespace ib {char b[100];} inline void pint(int x) { if(x==0) {pc(48); return;} if(x<0) {pc('-'); x=-x;} char *s=ib::b; while(x) *(++s)=x%10, x/=10; while(s!=ib::b) pc((*(s--))+48); } G otr; int main() { cst::s=&otr; otr.n=gi; int m=gi,q=gi; for(int i=1;i<=m;i++) { int a=gi, b=gi, c=gi; otr.adde(a,b,c); } cst::pre(); while(q--) { int a=gi,b=gi; printf("%lld\n",cst::query(a,b)); } }
注意这里tarjan函数用了一些奇技淫巧...实现的时候发现的
比如我们现在要找环,我们找到了这些点,那么边权怎么找呢?
我们可以发现例如a b c d,一定是a搜到b,b搜到c,c搜到d。这样我们只要记一下每一个点搜过来的那条边的边权就行了。注意到d到a这条边的边权我们好像没法确定,我们在d这个点上打个标记,最后再扫描一下a这个点的边,把这个边权补上。
B. bzoj4316
给出一个仙人掌森林(就是说不一定联通),求最大独立集。
感人至深的仙人掌上dp啊。
首先我们先明确一下这类dp的思路,就是说我们先考虑这个树的情况,然后考虑在尽量不改方程的情况下处理环的情况。
好,那么现在有棵树,我们就类似这样dp,记f[x][0/1]为x不选/选时这棵子树内的最大独立集,枚举所有孩子计算一下,类似这样:
简洁优雅的dp。
现在我们有了喜闻乐见的方点,我们考虑如果圆点的dp方程不变,方点的dp就应该是:dp[x][0]表示这个点的父亲选,dp[x][1]表示这个点的父亲可以选也可以不选。
那我们就枚举这个点的父亲选不选,在环上跑一个简单的dp就行了。
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first #define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);} #define es(x,e) (int e=fst[x];e;e=nxt[e]) #define SZ 666666 //don't pass directly in arguments! struct G { int n,M,fst[SZ],vb[SZ],nxt[SZ]; G() {M=0; n=0;} void ad_de(int a,int b) { ++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b; } void adde(int a,int b) { ad_de(a,b); ad_de(b,a); } }; //CST=Circle-Square-Tree namespace cst { G* s; //source int M,n,fst[SZ],vb[SZ],nxt[SZ]; void ad_de(int a,int b) { ++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b; } void adde(int a,int b) { ad_de(a,b); ad_de(b,a); } int ss[SZ],sn=0,C=0,dfn[SZ],low[SZ]; int rot[SZ]; vector<int> hs[SZ]; void tarjan(int x) { dfn[x]=low[x]=++C; ss[++sn]=x; for(int e=s->fst[x];e;e=s->nxt[e]) { int b=s->vb[e]; if(dfn[b]) {low[x]=min(low[x],dfn[b]); continue;} tarjan(b); low[x]=min(low[x],low[b]); if(dfn[x]<=low[b]) { if(ss[sn]==b) {adde(x,b); --sn; continue;} int g=++n; rot[g]=x; while(1) { int cur=ss[sn--]; adde(g,cur); hs[g].push_back(cur); if(cur==b) break; } adde(g,x); hs[g].push_back(x); } } } bool vis[SZ]; int dp[SZ][2]; int fpos(int p,int x) { vector<int> &h=hs[p]; int l=0,r=h.size()-1; while(l<r) { int mid=(l+r)>>1; if(dfn[h[mid]]>=dfn[x]) r=mid; else l=mid+1; } return l; } int tmp[SZ][2]; void dfs(int x,int f=0) { if(vis[x]) return; vis[x]=1; if(x<=s->n) //circle { dp[x][1]=1; dp[x][0]=0; for es(x,e) { int b=vb[e]; if(b==f) continue; dfs(b,x); dp[x][1]+=dp[b][0]; dp[x][0]+=max(dp[b][0],dp[b][1]); } } else //square { for es(x,e) { int b=vb[e]; if(b==f) continue; dfs(b,x); } vector<int> &h=hs[x]; int fp=fpos(x,f),s=h.size(); tmp[0][0]=0; tmp[0][1]=-1000000000; for(int i=1;i<s;i++) { int r=h[(i+fp)%s]; tmp[i][1]=tmp[i-1][0]+dp[r][1]; tmp[i][0]=max(tmp[i-1][0],tmp[i-1][1])+dp[r][0]; } dp[x][1]=max(tmp[s-1][1],tmp[s-1][0]); tmp[0][0]=-1000000000; tmp[0][1]=0; for(int i=1;i<s;i++) { int r=h[(i+fp)%s]; tmp[i][1]=tmp[i-1][0]+dp[r][1]; tmp[i][0]=max(tmp[i-1][0],tmp[i-1][1])+dp[r][0]; } dp[x][0]=tmp[s-1][0]; } } void pre() { n=s->n; M=0; for(int i=1;i<=s->n;i++) if(!dfn[i]) tarjan(i); for(int i=s->n+1;i<=n;i++) reverse(hs[i].begin(),hs[i].end()); for(int i=1;i<=n;i++) if(!vis[i]) dfs(i); int ans=0; for(int i=1;i<=n;i++) ans=max(ans,max(dp[i][0],dp[i][1])); printf("%d\n",ans); } } #define gc getchar() int g_i() { int tmp=0; bool fu=0; char s; while(s=gc,s!='-'&&(s<'0'||s>'9')) ; if(s=='-') fu=1; else tmp=s-'0'; while(s=gc,s>='0'&&s<='9') tmp=tmp*10+s-'0'; if(fu) return -tmp; else return tmp; } #define gi g_i() #define pob #define pc(x) putchar(x) namespace ib {char b[100];} inline void pint(int x) { if(x==0) {pc(48); return;} if(x<0) {pc('-'); x=-x;} char *s=ib::b; while(x) *(++s)=x%10, x/=10; while(s!=ib::b) pc((*(s--))+48); } G otr; int main() { cst::s=&otr; otr.n=gi; int m=gi; for(int i=1;i<=m;i++) { int a=gi, b=gi; otr.adde(a,b); } cst::pre(); }
C. bzoj1023
求一棵仙人掌的直径,边权为1。(输入格式十分奇葩,不过没有什么卵用)
对于树的情况大家都会dp吧!
每个点记录它儿子往上的链最长的和次长的,用最长的+次长的更新答案,把最长的记下来继续转移。
接下来对于方点的情况,那我们就要考虑它父亲往下的路径最长值,以及更新答案。
它父亲往下的路径最长值这个我们直接暴力枚举所有点算下长度统计即可。
接下来考虑更新答案,假设原来有0 1 2 3 4 ... s这么多点。
现在我们拷贝一份,变成0 1 2 3 4 ... s 0 1 2 3 4 ... s。
对于一个点x,拷贝一份之后的就可以和[x+1...x+s-1]组在一块。
我们目测一下,发现x与j∈[x+1...x+s/2]直接走坐标之差(j-i)比较近,与j∈[x+s/2+1,x+s-1]绕外面一圈(i-j+s)走比较近。
反正多个log也没什么事,我们拿个数据结构过来维护一下就行了(当然用单调队列复杂度更加靠谱)
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first #define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);} #define es(x,e) (int e=fst[x];e;e=nxt[e]) #define SZ 666666 template<class T> void gmax(T& a,T b){if(a<b) a=b;} template<class T> void gmin(T& a,T b){if(a>b) a=b;} //don't pass directly in arguments! struct G { int n,M,fst[SZ],vb[SZ],nxt[SZ]; G() {M=0; n=0;} void ad_de(int a,int b) { ++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b; } void adde(int a,int b) { ad_de(a,b); ad_de(b,a); } }; //CST=Circle-Square-Tree namespace cst { G* s; //source int M,n,fst[SZ],vb[SZ],nxt[SZ]; void ad_de(int a,int b) { ++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b; } void adde(int a,int b) { ad_de(a,b); ad_de(b,a); } int ss[SZ],sn=0,C=0,dfn[SZ],low[SZ]; int rot[SZ]; vector<int> hs[SZ]; void tarjan(int x) { dfn[x]=low[x]=++C; ss[++sn]=x; for(int e=s->fst[x];e;e=s->nxt[e]) { int b=s->vb[e]; if(dfn[b]) {low[x]=min(low[x],dfn[b]); continue;} tarjan(b); low[x]=min(low[x],low[b]); if(dfn[x]<=low[b]) { if(ss[sn]==b) {adde(x,b); --sn; continue;} int g=++n; rot[g]=x; while(1) { int cur=ss[sn--]; adde(g,cur); hs[g].push_back(cur); if(cur==b) break; } adde(g,x); hs[g].push_back(x); } } } bool vis[SZ]; int fpos(int p,int x) { vector<int> &h=hs[p]; int l=0,r=h.size()-1; while(l<r) { int mid=(l+r)>>1; if(dfn[h[mid]]>=dfn[x]) r=mid; else l=mid+1; } return l; } //rmq start from 0 struct rmqer { int rm[233333][40],gs[233333],t[233333]; void initst(int n) { int* a=t; --a; for(int i=1;i<=n;i++) rm[i][0]=a[i]; for(int s=1;(1<<s)<=n;s++) { for(int i=1;i+(1<<s)-1<=n;i++) rm[i][s]=max(rm[i][s-1],rm[i+(1<<(s-1))][s-1]); } for(int i=1;i<=n;i++) { int gl=1,s=0; while(gl<=i) gl<<=1, ++s; gs[i]=s-1; } } int query(int l,int r) { ++l; ++r; int s=gs[r-l+1]; int p=max(rm[l][s],rm[r-(1<<s)+1][s]); return p; } }r1,r2; int dp[SZ],rs[SZ]; void dfs(int x,int f=0) { if(vis[x]) return; vis[x]=1; if(x<=s->n) //circle { int ma=0,fm=0; for es(x,e) { int b=vb[e]; if(b==f) continue; dfs(b,x); int p=dp[b]+1; if(p>=ma) fm=ma, ma=p; else if(p>=fm) fm=p; } dp[x]=ma; rs[x]=ma+fm; } else //square { for es(x,e) { int b=vb[e]; if(b==f) continue; dfs(b,x); } vector<int> &h=hs[x]; int fp=fpos(x,f),s=h.size(); for(int i=1;i<s;i++) { int r=h[(i+fp)%s],d=min(i,s-i)-1; dp[x]=max(dp[x],d+dp[r]); } for(int i=0;i<s+s;i++) r1.t[i]=dp[h[(i+fp)%s]]+i; for(int i=0;i<s+s;i++) r2.t[i]=dp[h[(i+fp)%s]]-i; r1.initst(s+s); r2.initst(s+s); for(int i=0;i<s;i++) { int f1=i+s/2,f2=i+s-1; //for j∈[i+1,f1] dis=j-i //for j∈[f1+1,f2] dis=i-j+s if(i+1<=f1) gmax(rs[x],r1.query(i+1,f1)-i+dp[h[(i+fp)%s]]); if(f1+1<=f2) gmax(rs[x],r2.query(f1+1,f2)+i+s+dp[h[(i+fp)%s]]); } } } void pre() { n=s->n; M=0; for(int i=1;i<=s->n;i++) if(!dfn[i]) tarjan(i); for(int i=s->n+1;i<=n;i++) reverse(hs[i].begin(),hs[i].end()); for(int i=1;i<=n;i++) if(!vis[i]) dfs(i); int ans=0; for(int i=1;i<=n;i++) ans=max(ans,rs[i]); printf("%d\n",ans); } } #define gc getchar() int g_i() { int tmp=0; bool fu=0; char s; while(s=gc,s!='-'&&(s<'0'||s>'9')) ; if(s=='-') fu=1; else tmp=s-'0'; while(s=gc,s>='0'&&s<='9') tmp=tmp*10+s-'0'; if(fu) return -tmp; else return tmp; } #define gi g_i() #define pob #define pc(x) putchar(x) namespace ib {char b[100];} inline void pint(int x) { if(x==0) {pc(48); return;} if(x<0) {pc('-'); x=-x;} char *s=ib::b; while(x) *(++s)=x%10, x/=10; while(s!=ib::b) pc((*(s--))+48); } G otr; int tmp[SZ]; int main() { cst::s=&otr; otr.n=gi; int m=gi; for(int i=1;i<=m;i++) { int k=gi; for(int j=0;j<k;j++) tmp[j]=gi; for(int j=1;j<k;j++) otr.adde(tmp[j-1],tmp[j]); } cst::pre(); }
C. uoj87
给定一棵边带权的仙人掌。每次询问给定一个点集,求这个点集中点两两距离最大值。
先按A那样建出一棵带权圆方树,然后我们在这个点集上面建出虚树。
鬼畜的是虚树上面可能有一些鬼畜的圆方边和方方边。
为了比较和谐,我们考虑虚树上面的每个点。
如果虚树上面一个方点的父亲不是圆方树上的父亲,就把圆方树上的父亲加入虚树。
如果虚树上面一个圆点的父亲是方点而且不是圆方树上的父亲,就把圆方树上的父亲加入虚树。
这样进行喜闻乐见的树形dp就行了,还是拿个rmq维护。
注意tarjan的那个dfn不要作死在建虚树的时候用(一个是仙人掌的,一个是圆方树的)。
由于复杂度多了一个log用时光荣垫底。
(Q:怎么把log去掉?A:首先可以把找环的位置那个函数改成O(1)的,只需要判一下是否是环根即可。然后rmq的那个log也可以去掉,用单调队列,不过往上跳的那个log和sort的log显然去不掉)
写(调)了两天...前方高能预警
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first #define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);} #define es(x,e) (int e=fst[x];e;e=nxt[e]) #define SZ 1200010 #define SM 300010 #define S2 600010 template<class T> void gmax(T& a,T b){if(a<b) a=b;} template<class T> void gmin(T& a,T b){if(a>b) a=b;} #define gc getchar() int g_i() { int tmp=0; bool fu=0; char s; while(s=gc,s!='-'&&(s<'0'||s>'9')) ; if(s=='-') fu=1; else tmp=s-'0'; while(s=gc,s>='0'&&s<='9') tmp=tmp*10+s-'0'; if(fu) return -tmp; else return tmp; } #define gi g_i() #define pc(x) putchar(x) namespace ib {char b[100];} inline void pll(ll x) { if(x==0) {pc(48); return;} if(x<0) {pc('-'); x=-x;} char *s=ib::b; while(x) *(++s)=x%10, x/=10; while(s!=ib::b) pc((*(s--))+48); } struct G { int n,M,fst[SM],vb[SZ],vc[SZ],nxt[SZ]; G() {M=0; n=0;} void ad_de(int a,int b,int c) { ++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b; vc[M]=c; } void adde(int a,int b,int c) { ad_de(a,b,c); ad_de(b,a,c); } }; namespace cst { G* s; int M,n,fst[S2],vb[SZ],nxt[SZ]; ll vc[SZ]; void ad_de(int a,int b,ll c) { ++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b; vc[M]=c; } void adde(int a,int b,ll c) { ad_de(a,b,c); ad_de(b,a,c); } int ss[S2],sn=0,C=0,dfn[S2],low[S2],fe[S2]; int rot[S2],tag[S2]; ll cl[S2]; vector<int> hs[S2],ls[S2]; vector<ll> qzl[S2]; void tarjan(int x) { dfn[x]=low[x]=++C; ss[++sn]=x; for(int e=s->fst[x];e;e=s->nxt[e]) { int b=s->vb[e]; if(dfn[b]) {low[x]=min(low[x],dfn[b]); continue;} fe[b]=s->vc[e]; tarjan(b); low[x]=min(low[x],low[b]); if(dfn[x]<=low[b]) { if(ss[sn]==b) {adde(x,b,s->vc[e]); --sn; continue;} int g=++n; rot[g]=x; tag[ss[sn]]=g; ll tl=0; while(1) { int cur=ss[sn--]; hs[g].push_back(cur); ls[g].push_back(fe[cur]); tl+=fe[cur]; if(cur==b) break; } hs[g].push_back(x); ls[g].push_back(-1); cl[g]=tl; } } for(int e=s->fst[x];e;e=s->nxt[e]) { int b=s->vb[e]; if(!tag[b]) continue; int r=tag[b]; cl[r]+=s->vc[e]; ls[r][ls[r].size()-1]=s->vc[e]; tag[b]=0; } } #define S 21 ll dc[S2]; int fa[S2],p[S2][S],sz[S2],dep[S2],dfn2[S2]; void dfs(int x,int f=0) { sz[x]=1; dfn2[x]=++C; for es(x,e) { int b=vb[e]; if(b==f) continue; fa[b]=p[b][0]=x; dep[b]=dep[x]+1; dc[b]=dc[x]+vc[e]; dfs(b,x); sz[x]+=sz[b]; } } int jump(int x,int d) { for(int s=S-1;s>=0;s--) { if(p[x][s]&&dep[p[x][s]]>=d) x=p[x][s]; } if(dep[x]!=d) exit(-1); return x; } int lca(int a,int b) { if(dep[a]>dep[b]) swap(a,b); b=jump(b,dep[a]); if(a==b) return a; for(int s=S-1;s>=0;s--) { if(p[a][s]!=p[b][s]) a=p[a][s], b=p[b][s]; } return p[a][0]; } ll dis(int a,int b) { int l=lca(a,b); return dc[a]+dc[b]-dc[l]*2; } void pre() { n=s->n; M=0; for(int i=1;i<=s->n;i++) if(!dfn[i]) tarjan(i); for(int i=s->n+1;i<=n;i++) reverse(hs[i].begin(),hs[i].end()), reverse(ls[i].begin(),ls[i].end()); for(int i=s->n+1;i<=n;i++) { ll len=-ls[i][0]; for(int j=0;j<hs[i].size();j++) { len+=ls[i][j]; qzl[i].push_back(len); adde(i,hs[i][j],min(len,cl[i]-len)); } } for(int i=1;i<=n;i++) if(!fa[i]) dfs(i); for(int i=1;i<S;i++) { for(int j=1;j<=n;j++) p[j][i]=p[p[j][i-1]][i-1]; } } int fpos(int p,int x) { vector<int> &h=hs[p]; int l=0,r=h.size()-1; while(l<r) { int mid=(l+r)>>1; if(dfn[h[mid]]>=dfn[x]) r=mid; else l=mid+1; } if(h[l]==x) return l; return -1; } namespace vt { #define f_ first #define s_ second typedef pair<int,int> pii; int sn,ss[S2],vn,vs[S2],stn=0,rot=0; int st[S2],vfa[S2]; bool cmp_dfsn(int a,int b) {return dfn2[a]<dfn2[b];} int M,fst[S2],vb[SZ],nxt[SZ]; ll vc[SZ]; void ad_de(int a,int b,ll c) { ++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b; vc[M]=c; } void adde(int a,int b,ll c) { ad_de(a,b,c); ad_de(b,a,c); } ll dp[S2],rs[S2]; bool vis[S2]; void gg() { rot=M=0; sn=gi; vn=stn=0; for(int i=1;i<=sn;i++) ss[i]=gi; sort(ss+1,ss+1+sn,cmp_dfsn); sn=unique(ss+1,ss+1+sn)-ss-1; for(int i=1;i<=sn;i++) vs[++vn]=ss[i]; for(int i=1;i<=sn;i++) { int x=ss[i]; if(!stn) {st[++stn]=x; vfa[x]=0; continue;} int lc=lca(x,st[stn]); for(;dep[st[stn]]>dep[lc];--stn) { if(dep[st[stn-1]]<=dep[lc]) vfa[st[stn]]=lc; } if(st[stn]!=lc) { vs[++vn]=lc; vfa[lc]=st[stn]; st[++stn]=lc; } vfa[x]=lc; st[++stn]=x; } for(int i=1;i<=vn;i++) { if(vs[i]>s->n&&vfa[vs[i]]&&vfa[vs[i]]!=fa[vs[i]]) { int tmp=fa[vs[i]]; vs[++vn]=tmp; vfa[tmp]=vfa[vs[i]]; vfa[vs[i]]=tmp; } } for(int i=1;i<=vn;i++) { if(vs[i]<=s->n&&vfa[vs[i]]>s->n&&fpos(vfa[vs[i]],vs[i])==-1) { int tmp=jump(vs[i],dep[vfa[vs[i]]]+1); vs[++vn]=tmp; vfa[tmp]=vfa[vs[i]]; vfa[vs[i]]=tmp; } } for(int i=1;i<=vn;i++) { if(!rot||dep[vs[i]]<dep[rot]) rot=vs[i]; } for(int i=1;i<=vn;i++) fst[vs[i]]=vis[vs[i]]=rs[vs[i]]=dp[vs[i]]=0; for(int i=1;i<=vn;i++) { if(vfa[vs[i]]) adde(vs[i],vfa[vs[i]],dis(vs[i],vfa[vs[i]])); } } struct rmqer { ll rm[SZ][21],gs[SZ],t[SZ]; void initst(int n) { ll* a=t; --a; for(int i=1;i<=n;i++) rm[i][0]=a[i]; for(int s=1;(1<<s)<=n;s++) { for(int i=1;i+(1<<s)-1<=n;i++) rm[i][s]=max(rm[i][s-1],rm[i+(1<<(s-1))][s-1]); } for(int i=1;i<=n;i++) { int gl=1,s=0; while(gl<=i) gl<<=1, ++s; gs[i]=s-1; } } ll query(int l,int r) { ++l; ++r; int s=gs[r-l+1]; ll p=max(rm[l][s],rm[r-(1<<s)+1][s]); return p; } }r1,r2; ll discyc_(int r,int a,int b) { int pa=fpos(r,a),pb=fpos(r,b); ll qq=qzl[r][pb]-qzl[r][pa]; if(qq<0) qq+=cl[r]; return qq; } ll discyc(int r,int a,int b) { ll l=discyc_(r,a,b); return min(l,cl[r]-l); } pair<ll,int> rp[SZ]; void dfs(int x,int f=0) { if(vis[x]) return; vis[x]=1; if(x<=s->n) //circle { dp[x]=-100000000000000000LL; ll ma=0,fm=0; for es(x,e) { int b=vb[e]; if(b==f) continue; dfs(b,x); ll p=dp[b]+vc[e]; if(p>=ma) fm=ma, ma=p; else if(p>=fm) fm=p; } dp[x]=ma; rs[x]=ma+fm; } else //square { for es(x,e) { int b=vb[e]; if(b==f) continue; dfs(b,x); } dp[x]=-100000000000000000LL; if(f) { for es(x,e) { int b=vb[e]; if(b==f) continue; dp[x]=max(dp[x],discyc(x,f,b)-dis(f,x)+dp[b]); } } int s=0,sr=vb[fst[x]]; for(int e=fst[x],i=0;e;e=nxt[e],++i) s=i+1,rp[i].se=vb[e],rp[i].fi=discyc_(x,sr,rp[i].se); sort(rp,rp+s); for(int i=s;i<s+s;i++) rp[i]=rp[i-s], rp[i].fi+=cl[x]; for(int i=0;i<s+s;i++) { ll l=rp[i].fi; r1.t[i]=dp[rp[i%s].se]+l; r2.t[i]=dp[rp[i%s].se]-l; } r1.initst(s+s); r2.initst(s+s); int cur=0; for(int i=0;i<s;i++) { int f2=i+s-1; ll ttt; while(ttt=rp[cur].fi-rp[i].fi, ttt<cl[x]-ttt&&cur<=f2) ++cur; int f1=cur-1; ll l=rp[i].fi; if(i+1<=f1) gmax(rs[x],r1.query(i+1,f1)-l+dp[rp[i].se]); if(f1+1<=f2) gmax(rs[x],r2.query(f1+1,f2)+l+cl[x]+dp[rp[i].se]); } } } void gans() { dfs(rot); ll ans=0; for(int i=1;i<=vn;i++) ans=max(ans,rs[vs[i]]); pll(ans); pc(10); } } } G otr; struct edg {int a,b,c;}es[S2]; bool operator < (edg a,edg b) { if(a.a!=b.a) return a.a<b.a; return a.b<b.b; } int main() { cst::s=&otr; otr.n=gi; int m=gi; for(int i=1;i<=m;i++) { es[i].a=gi, es[i].b=gi, es[i].c=gi; if(es[i].a>es[i].b) swap(es[i].a,es[i].b); } sort(es+1,es+1+m); for(int i=1;i<=m;i++) { if(es[i].a==es[i+1].a&&es[i].b==es[i+1].b) { es[i+1].c=min(es[i+1].c,es[i].c); continue; } otr.adde(es[i].a,es[i].b,es[i].c); } cst::pre(); int q=gi; while(q--) { cst::vt::gg(); cst::vt::gans(); } }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号