十连测泛做 题解
deep
一棵n个点的树上有k个点有果实,现在要删去一些边使最大联通块最小且每个联通块都有果实,求这个联通块数量最小值。k<=n<=200000。
不妨二分答案。我们考虑x所在的子树,x所在的联通块大小最小是多少。注意到x的子树如果可以在答案内包含关键点就一定要包含,那我们就让f[x]为联通块大小,可以包含关键点为正,否则为负。
如果x是关键点,那么只要累加所有孩子里负的f即可,如果爆了显然这个最小值就不合法。
如果x不是关键点,考虑它一定要连上孩子中f最小的正的,然后所有孩子里负的再连上去。如果这样已经爆了,那就只能让它和所有负的在一起,f值就为负,如果还爆了那就不合法。
啊还有下面的这个代码会爆栈。。。开栈:-Wl,--stack=268435456
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair #define pii pair<int,int> #define ll long long #define ld double #define vi vector<int> #define fi first #define se second #define fe first #define SZ 666666 int M=0,fst[SZ],vb[SZ],nxt[SZ],n,m,dp[SZ]; bool gs[SZ],ok=1; void ad_de(int a,int b) {++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b;} int inf=1000000000; void dfs(int x,int f=0) { bool gj=gs[x]; int sum=1,minn=inf; for(int e=fst[x];e;e=nxt[e]) { int b=vb[e]; if(b==f) continue; dfs(b,x); if(dp[b]<0) sum-=dp[b]; if(gj||dp[b]<0) continue; minn=min(minn,dp[b]); } if(minn+sum>m) minn=inf; if(gj) dp[x]=(sum<=m)?sum:(ok=0,-inf); else dp[x]=(minn!=inf)?(minn+sum):(-sum); } int main() { freopen("deep.in","r",stdin); freopen("deep.out","w",stdout); int k; scanf("%d%d",&n,&k); for(int i=1;i<n;i++) { int a,b; scanf("%d%d",&a,&b); ad_de(a,b); ad_de(b,a); } for(int i=1;i<=k;i++) { int x; scanf("%d",&x); gs[x]=1; } int l=0,r=n; while(l<r) { m=(l+r)>>1; ok=1; dfs(1); ok&=dp[1]>0; if(ok) r=m; else l=m+1; } printf("%d\n",l); }
dark
n个点的无向图,每条边都可能存在,一个图的权值是连通块个数的m次方,求所有可能的图的权值和。答案对998244353取模。多组数据,T<=1000,n<=30000,m<=15。
啊一看就是fft题,首先我们来翻翻彭老师的博客发现一个好玩的东西:
http://picks.logdown.com/posts/189620-inverse-element-of-polynomial
看起来很有道理,那我们就可以求出n个点的无向连通图个数。
然后接下来就不会了,贴一波题解
嗯很有道理。。。
然后答案似乎可以这样计算:
那么可以把j提出来变成这样:
后面的东西是一个跟n和j有关的量。
那么只要对于每次询问枚举j即可。
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <algorithm> #include <vector> using namespace std; #define ll long long #define pb push_back ll MOD=998244353; #define SZ 666666 ll w[2][SZ]; ll qp(ll a,ll b) { ll ans=1; while(b) { if(b&1) ans=ans*a%MOD; a=a*a%MOD; b>>=1; } return ans; } int K; void fftinit(int n) { for(K=1;K<n;K<<=1); w[0][0]=w[0][K]=1; ll g=qp(3,(MOD-1)/K); //3是原根 for(int i=1;i<K;i++) w[0][i]=w[0][i-1]*g%MOD; for(int i=0;i<=K;i++) w[1][i]=w[0][K-i]; } void fft(int* x,int v) { for(int i=0,j=0;i<K;i++) { if(i>j) {x[i]^=x[j]; x[j]^=x[i]; x[i]^=x[j];} for(int l=K>>1;(j^=l)<l;l>>=1); } for(int i=2;i<=K;i<<=1) { for(int j=0;j<K;j+=i) { for(int l=0;l<i>>1;l++) { ll t=(ll)x[j+l+(i>>1)]*w[v][K/i*l]%MOD; x[j+l+(i>>1)]=((x[j+l]-t)%MOD+MOD)%MOD; x[j+l]=(x[j+l]+t)%MOD; } } } if(!v) return; ll rv=qp(K,MOD-2); for(int i=0;i<K;i++) x[i]=x[i]*rv%MOD; } struct poly { vector<int> ps; int cs() {return ps.size()-1;} int& operator [] (int x) {return ps[x];} //ps.at(x) void sc(int x) {ps.resize(x+1);} void dbg() { bool fi=0; for(int i=cs();i>=0;i--) { if(!ps[i]) continue; if(fi) { if(i==0) printf("+%d",ps[i]); else if(ps[i]==1) printf("+"); else if(ps[i]==-1) printf("-"); else printf("+%d",ps[i]); } else { if(i==0) printf("%d",ps[i]); else if(ps[i]==1); else if(ps[i]==-1) printf("-"); else printf("%d",ps[i]); } if(i>1) printf("x^%d",i); else if(i==1) printf("x"); fi=1; } if(!fi) printf("0"); putchar(10); } void clr() { int p=cs()+1; while(p&&!ps[p-1]) --p; sc(p-1); } }; ll gm(ll x) { x=x%MOD; if(x<0) x+=MOD; return x; } namespace PolyMul{int ta[SZ],tb[SZ],tc[SZ];} poly operator * (poly a,poly b) { using namespace PolyMul; if(a.cs()<200||b.cs()<200) { poly g; g.sc(a.cs()+b.cs()); for(int i=0;i<=a.cs();i++) { for(int j=0;j<=b.cs();j++) g[i+j]=gm(g[i+j]+a[i]*(ll)b[j]%MOD); } return g; } poly c; int t=a.cs()+b.cs(); c.sc(t); fftinit(t+1); memset(ta,0,sizeof(int)*K); memset(tb,0,sizeof(int)*K); memset(tc,0,sizeof(int)*K); for(int i=a.cs();i>=0;i--) ta[i]=a[i]; for(int i=b.cs();i>=0;i--) tb[i]=b[i]; fft(ta,0); fft(tb,0); for(int i=0;i<K;i++) tc[i]=(ll)ta[i]*tb[i]%MOD; fft(tc,1); for(int i=t;i>=0;i--) c[i]=tc[i]; c.clr(); return c; } namespace PolyInv{int ay[SZ],a0[SZ],tmp[SZ];} void ginv(int t) { using namespace PolyInv; if(t==1) {a0[0]=qp(ay[0],MOD-2); return;} ginv((t+1)>>1); fftinit(t+t+3); memset(tmp,0,sizeof(int)*K); for(int i=t;i<K;i++) tmp[i]=a0[i]=0; for(int i=0;i<t;i++) tmp[i]=ay[i]; fft(tmp,0); fft(a0,0); for(int i=0;i<K;i++) a0[i]=gm((2-(ll)tmp[i]*a0[i])%MOD*a0[i]); fft(a0,1); for(int i=t;i<K;i++) a0[i]=0; } poly inv(poly x) { using namespace PolyInv; poly y; y.sc(x.cs()); for(int i=x.cs();i>=0;i--) ay[i]=x[i]; ginv(x.cs()+1); for(int i=x.cs();i>=0;i--) y[i]=a0[i]; y.clr(); return y; } ll H(ll x) { return qp(2,x*(x-1)/2); } ll h[SZ],g[SZ],fac[SZ],rfac[SZ],ny[SZ]; int gi[SZ]; ll C(ll a,ll b) { return fac[a]*rfac[a-b]%MOD*rfac[b]%MOD; } int G[18][66666],tmp[SZ]; ll s[18][18]; #define P 30002 int main() { freopen("dark.in","r",stdin); freopen("dark.out","w",stdout); fac[0]=rfac[0]=1; for(int i=1;i<=P;i++) ny[i]=qp(i,MOD-2); for(int i=1;i<=P;i++) fac[i]=fac[i-1]*(ll)i%MOD, rfac[i]=rfac[i-1]*(ll)ny[i]%MOD; for(int i=1;i<=P;i++) h[i]=H(i); poly a; a.sc(P-1); a[0]=1; for(int i=1;i<P;i++) a[i]=h[i]*(ll)rfac[i]%MOD; poly c; c.sc(P-1); for(int i=1;i<P;i++) c[i]=h[i]*(ll)rfac[i-1]%MOD; poly b=inv(a)*c; gi[0]=0; for(int i=1;i<=P;i++) g[i]=fac[i-1]*(ll)b[i]%MOD, gi[i]=g[i]*(ll)rfac[i]%MOD; for(int i=0;i<=P;i++) G[0][i]=h[i]*(ll)rfac[i]%MOD; G[0][0]=1; fftinit(P+P); fft(gi,0); for(int j=1;j<=15;j++) { for(int i=0;i<K;i++) tmp[i]=G[j-1][i]; fft(tmp,0); for(int i=0;i<K;i++) G[j][i]=tmp[i]*(ll)gi[i]%MOD; fft(G[j],1); for(int i=P;i<K;i++) G[j][i]=0; } s[0][0]=1; for(int i=1;i<=15;i++) { for(int j=1;j<=15;j++) s[i][j]=(j*(ll)s[i-1][j]%MOD+s[i-1][j-1])%MOD; } int T,n,m; scanf("%d",&T); while(T--) { scanf("%d%d",&n,&m); ll ans=0; for(int i=0;i<=m;i++) ans+=s[m][i]*fac[n]%MOD*G[i][n]%MOD, ans%=MOD; ans=(ans%MOD+MOD)%MOD; printf("%d\n",int(ans)); } }
huffman
n<=100000。
这个题解十分显然吧...就算不知道也可以调a的值试出来。
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first typedef long long ll; ll MOD=1000000007; #define SZ 666666 int n,a[SZ]; ll qp(ll a,ll b) { ll ans=1; a%=MOD; while(b) { if(b&1) ans=ans*a%MOD; a=a*a%MOD; b>>=1; } return ans; } int main() { freopen("huffman.in","r",stdin); freopen("huffman.out","w",stdout); scanf("%d",&n); ll qaq=0,qwq=0,mul=1; for(int i=1;i<=n;i++) scanf("%d",a+i), qwq+=a[i], qwq%=MOD; for(int i=2;i<=n;i++) qaq=qaq+qp(i,MOD-2)*2%MOD, qaq%=MOD; for(int i=2;i<=n;i++) mul=mul*((i*ll(i-1)/2)%MOD)%MOD; ll ans=qaq*qwq%MOD*mul%MOD; printf("%d\n",int(ans)); }
segment
n,m,q,ai,v<=10^5。
首先,在经过一系列操作后,数组中每个位置上的数都可以对应为原数组中某一段区间的最大值。
我们考虑一个暴力平方做法,每次我们考虑这个位置对应的当前区间最大值,倒着考虑R~L的修改,每次这个区间如果和修改区间有交就取并集。
然后我们考虑把这个算法用数据结构进行优化...
我们注意到可以将左端点和右端点分开看,以左端点为例,也就是需要不停计算前一个覆盖到这个端点的操作,然后把位置挪到那个操作的左端点。
我们遍历所有操作,每一次计算前一个覆盖到这个操作左端点的操作可以拿一个可持久化线段树(主席树)来维护,每一次只要兹磁可持久化区间赋值就行了。
之后我们拿一个倍增数组来维护一下左端点右端点跳2^x步到哪里。
对于一个询问,我们在r结束之后的可持久化线段树上查询一下覆盖到这个东西的第一个操作是什么,如果小于l就算了,否则我们找到这个操作,跳跳跳,找到对应最大值的区间,再找个线段树查查就行了。
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first #define SZ 666666 namespace SegA { int M=131072,maxn[SZ],*xs=maxn+M; void init() { for(int i=M-1;i>=1;i--) maxn[i]=max(maxn[i+i+1],maxn[i+i]); } void upd(int p) { for(int i=(p+M)>>1;i>=1;i>>=1) maxn[i]=max(maxn[i+i+1],maxn[i+i]); } int qmax(int l,int r) { int ans=0; for(l+=M-1,r+=M+1;l^r^1;l>>=1,r>>=1) { if(~l&1) ans=max(ans,maxn[l^1]); if(r&1) ans=max(ans,maxn[r^1]); } return ans; } } #define A_ SegA:: #define S2 5555555 int n,m,q; int lc[S2],rc[S2],maxn[S2],rots[S2],an=0; #define S 100233 int ql,qr,qv; void edit(int r1,int& r2,int l,int r) { if(ql>r||qr<l) { r2=r1; return; } r2=++an; maxn[r2]=maxn[r1]; lc[r2]=lc[r1]; rc[r2]=rc[r1]; if(ql<=l&&r<=qr) { maxn[r2]=max(maxn[r2],qv); return; } int m=(l+r)>>1; edit(lc[r1],lc[r2],l,m); edit(rc[r1],rc[r2],m+1,r); } int qt,ans=0; void query(int x,int l,int r) { ans=max(ans,maxn[x]); if(l==r) return; int mid=(l+r)>>1; if(qt<=mid) query(lc[x],l,mid); else query(rc[x],mid+1,r); } int el[SZ],er[SZ]; int L[SZ][18],R[SZ][18]; int main() { freopen("segment.in","r",stdin); freopen("segment.out","w",stdout); scanf("%d%d%d",&n,&m,&q); for(int i=1;i<=n;i++) scanf("%d",A_ xs+i); A_ init(); for(int i=1;i<=m;i++) { scanf("%d%d",el+i,er+i); qt=el[i]; ans=0; query(rots[i-1],1,n); L[i][0]=ans; qt=er[i]; ans=0; query(rots[i-1],1,n); R[i][0]=ans; for(int j=1;j<=17;j++) L[i][j]=L[L[i][j-1]][j-1]; for(int j=1;j<=17;j++) R[i][j]=R[R[i][j-1]][j-1]; ql=el[i]; qr=er[i]; qv=i; edit(rots[i-1],rots[i],1,n); } while(q--) { int t; scanf("%d",&t); if(t==1) { int x,y; scanf("%d%d",&x,&y); A_ xs[x]=y; A_ upd(x); continue; } int l,r,p; scanf("%d%d%d",&l,&r,&p); qt=p; ans=0; query(rots[r],1,n); if(ans<l) ql=qr=p; else { ql=qr=ans; for(int i=17;i>=0;i--) if(L[ql][i]>=l) ql=L[ql][i]; for(int i=17;i>=0;i--) if(R[qr][i]>=l) qr=R[qr][i]; ql=el[ql]; qr=er[qr]; } printf("%d\n",A_ qmax(ql,qr)); } }
ants
有一根长度为m的绳子,在最初的时刻,上面分布着n只蚂蚁,每一只蚂蚁在最初都可能选择任意一个方向爬,爬行的速度始终为1,当有两只蚂蚁相遇时,它们会各自调转方向,以原有的速度继续爬行。每只蚂蚁随意选择一种方向一共有2^n种方案,每一种方案都存在一个时间使得最后一只蚂蚁恰好爬离绳子。现在求每一个这样的时间对应的方案数分别是多少。
使用数据生成器:
n<=500W。
这个题好陈啊...
当两个蚂蚁相遇时,我们不妨当作它们穿过去了继续爬行。
我们从小到大枚举答案,随手统计一下即可。
注意不能sort...
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first int n,x,a0,b0,c0; #define SZ 10000007 ll m,A[SZ],B[SZ],C[SZ]; inline int myrand() { x=(1ll*a0*x+b0)%c0; return x; } inline void init() { cin>>n>>x>>a0>>b0>>c0; for(int i=1;i<=(n+1)/2;i++)B[i]=B[i-1]+myrand()+5; m=B[(n+1)/2]<<1|1; for(int i=1;i<=n-(n+1)/2;i++)C[i]=m-(myrand()%(B[i]-B[i-1]-1)+B[i-1]+1); reverse(C+1,C+(n-(n+1)/2)+1); for(int i=1;i<=(n+1)/2;i++)A[i]=B[i]; for(int i=1;i<=n-(n+1)/2;i++)A[i+(n+1)/2]=C[i]; } ll MOD=1000000007; ll as[SZ],bs[SZ]; ll ts[SZ],tid[SZ]; int two[SZ]; int main() { freopen("ants.in","r",stdin); freopen("ants.out","w",stdout); init(); int p=0; for(int i=1;i<=n;i++) as[i]=A[i], bs[i]=m-A[i]; int a=1,b=n; while(a<=n&&b>=1) { if(as[a]<=bs[b]) ts[++p]=as[a], tid[p]=a, ++a; else ts[++p]=bs[b], tid[p]=b, --b; } while(a<=n) ts[++p]=as[a], tid[p]=a, ++a; while(b>=1) ts[++p]=bs[b], tid[p]=b, --b; ts[0]=ts[p+1]=-1; int cur=1,nok=n; ll rp=1,ans=0; for(int i=1;i<=p;i++) { ts[i]%=MOD; two[tid[i]]++; if(two[tid[i]]==1) --nok; if(ts[i]!=ts[i+1]&&!nok) ans=ans+rp*ts[i]%MOD, ans%=MOD; if(two[tid[i]]==2) rp=rp*2%MOD; } printf("%d\n",int(ans%MOD)); }
meizi
一棵赛艇的交互题~
一句话题意,交互,有2000*2000个格子,格子上有各不相同的数,要求找到一个格子比四周格子上数都大。
有一个方法是找2000个点随机爬山大概能得70分...
我们来想一个靠谱做法:
每次找到中间一列切开询问这列权值,找到一个最大的,如果左右都比中间小那么就搞定了。如果左边<右边就递归到右边,否则递归到左边。
代码简单明了
#include <bits/stdc++.h> #include "MXPOINT.h" using namespace std; typedef pair<int,int> pii; //int ask(int x,int y) int rr[2010][2010]; int ask(int x,int y) { if(rr[x][y]) return rr[x][y]; if((x<1)||(x>2000)||(y<1)||(y>2000)) return -1; return rr[x][y]=ASK(x,y); } int yl[2001]; pii fz(int l,int r) { int m=(l+r)>>1; for(int i=1;i<=2000;i++) yl[i]=ask(m,i); pii maxn; for(int i=1;i<=2000;i++) maxn=max(maxn,pii(yl[i],i)); int p=maxn.second,s=ask(m,p); int l_=ask(m-1,p),r_=ask(m+1,p); if(l_<maxn.first&&r_<maxn.first) return pii(m,p); if(l_<r_) return fz(m+1,r); else return fz(l,m-1); } pii FINDMXPOINT() { memset(rr,0,sizeof(rr)); return fz(1,2000); }
理论70,但出于某种原因(常数大)只拿了50分...不明觉厉
我们考虑一个比较靠谱的做法...
我们对两维轮流切分!不过之前那个做法那样做会wa(实测
我们先算出mxed表示当前矩阵的边界最大值(细节见代码),然后中间还是切一刀,最大值为mx。如果mx<mxed就递归到mxed一边。否则就和以前一样询问mx两边然后递归。
(最近代码风格越来越stl了,轻喷)
#include <bits/stdc++.h> #include "MXPOINT.h" using namespace std; typedef pair<int,int> pii; #define fi first #define se second #define fe first int rr[2010][2010]; int ask(int x,int y) { if(rr[x][y]) return rr[x][y]; if((x<1)||(x>2000)||(y<1)||(y>2000)) return -1; return rr[x][y]=ASK(x,y); } int dx[4]={-1,1,0,0},dy[4]={0,0,-1,1}; int yl[2001]; typedef pair<int,pii> rec; rec mrec(int x,int y) { return rec(ask(x,y),pii(x,y)); } pii fz(int x1,int x2,int y1,int y2) { //cerr<<"FZ"<<x1<<","<<x2<<","<<y1<<","<<y2<<"\n"; if(y2-y1<=3&&x2-x1<=3) { for(int x=x1;x<=x2;x++) { for(int y=y1;y<=y2;y++) { int maxn=0; for(int k=0;k<4;k++) maxn=max(maxn,ask(dx[k]+x,dy[k]+y)); if(maxn<ask(x,y)) return pii(x,y); } } assert(0); } rec rr; for(int y=y1-1;y<=y2+1;y++) rr=max(rr,mrec(x1-1,y)); for(int y=y1-1;y<=y2+1;y++) rr=max(rr,mrec(x2+1,y)); for(int x=x1-1;x<=x2+1;x++) rr=max(rr,mrec(x,y1-1)); for(int x=x1-1;x<=x2+1;x++) rr=max(rr,mrec(x,y2+1)); if(x2-x1>=y2-y1) //cut x axis { //cerr<<"CASE1\n"; int m=(x1+x2)>>1; rec midp; for(int j=y1;j<=y2;j++) midp=max(midp,mrec(m,j)); int mx=midp.fi; if(mx<rr.fi) { if(rr.se.fi<m) return fz(x1,m-1,y1,y2); else return fz(m+1,x2,y1,y2); } int l_=ask(m-1,midp.se.se); int r_=ask(m+1,midp.se.se); if(l_<mx&&r_<mx) return midp.se; if(l_>r_) return fz(x1,m-1,y1,y2); else return fz(m+1,x2,y1,y2); } else { //cerr<<"CASE2\n"; int m=(y1+y2)>>1; rec midp; for(int i=x1;i<=x2;i++) midp=max(midp,mrec(i,m)); int mx=midp.fi; if(mx<rr.fi) { if(rr.se.se<m) return fz(x1,x2,y1,m-1); else return fz(x1,x2,m+1,y2); } int l_=ask(midp.se.fi,m-1); int r_=ask(midp.se.fi,m+1); if(l_<mx&&r_<mx) return midp.se; if(l_>r_) return fz(x1,x2,y1,m-1); else return fz(x1,x2,m+1,y2); } } pii FINDMXPOINT() { memset(rr,0,sizeof(rr)); return fz(1,2000,1,2000); }
binary
维护一个集合,支持加入一个数和查询和给定的数字进行某种位运算(xor/and/or)能得到的最大值以及达到最大值的方案数。
n<=100000,0<=ai<=65535。
注意到ai只有16位,设f[i][j]为前8位为i的数与某个后8位为j的数进行位运算最大值及方案。插入和查询时随意弄弄即可。
//By zzq #include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <math.h> #include <set> #include <map> using namespace std; #define SZ 666666 int n,t; int f[1000][1000],g[1000][1000]; char op[233]; int opt(int a,int b) { if(op[0]=='a') return a&b; if(op[0]=='o') return a|b; if(op[0]=='x') return a^b; } void upd(int& F,int& G,int v,int c=1) { if(F>v||!c) return; if(F<v) F=v, G=0; G+=c; } #define upd2(x,y,v) upd(f[x][y],g[x][y],v) int main() { freopen("binary.in","r",stdin); freopen("binary.out","w",stdout); int M=1<<8; scanf("%d%s%d",&n,op,&t); for(int i=1;i<=n;i++) { int a; scanf("%d",&a); int b=a&(M-1); a>>=8; if(i>1) { int ff=-1,gg; for(int j=0;j<M;j++) upd(ff,gg,opt(j,a)<<8|f[j][b],g[j][b]); if(t==1) printf("%d %d\n",ff,gg); else printf("%d\n",ff); } for(int j=0;j<M;j++) upd2(a,j,opt(j,b)); } }
string
维护一个字符串,每次在一个历史字符串末尾插入一个字符成为一个新字符串,并输出新字符串最短循环节。n,m<=300000,强制在线。
考虑如果没有可持久化是一条链怎么做。我们可以进行kmp,ans=len-next(len)。(next就是fail)
现在我们可持久化一下这个kmp就gg了对吧...
那我们考虑维护一个trans数组,trans(x,y)表示如果下一个字符为y那么从x开始按照next来跳会跳到哪里可以匹配。
考虑我们现在在x状态后面加入了一个字符c成为了s状态,那么next(s)=trans(x,c),trans(s)=trans(next(s)),trans(x,c)=s。
那么我们随手可持久化一下就行。
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first #define S 20000003 #define SZ 666666 #define gc (getchar()) inline const int& ri(int& x) { int tmp=0; bool fu=0; char s; while(s=gc,s!='-'&&(s<'0'||s>'9')) ; if(s=='-') fu=1; else tmp=s-'0'; while(s=gc,s>='0'&&s<='9') tmp=tmp*10+s-'0'; if(fu) return x=-tmp; else return x=tmp; } inline int _gi() {int p; ri(p); return p;} #define gi _gi() int lc[S],rc[S],v[S],rot[SZ],an=0; int n,m,len[SZ]; int edit(int x,int l,int r,int p,int c) { int s=++an; if(l==r) {v[s]=c; return s;} int m=(l+r)>>1; if(p<=m) lc[s]=edit(lc[x],l,m,p,c), rc[s]=rc[x]; else lc[s]=lc[x], rc[s]=edit(rc[x],m+1,r,p,c); return s; } int query(int x,int l,int r,int p) { if(l==r) return v[x]; int m=(l+r)>>1; if(p<=m) return query(lc[x],l,m,p); else return query(rc[x],m+1,r,p); } int main() { freopen("string.in","r",stdin); freopen("string.out","w",stdout); int tp,lans=0; n=gi, m=gi, tp=gi; for(int i=1;i<=n;i++) { int x=gi, y=gi; x^=lans*tp; y^=lans*tp; len[i]=len[x]+1; int rxt=query(rot[x],0,n,x); int fail=query(rxt,1,m,y); printf("%d\n",lans=len[i]-len[fail]); rot[i]=edit(rot[x],0,n,x,edit(rxt,1,m,y,i)); rot[i]=edit(rot[i],0,n,i,query(rot[i],0,n,fail)); } }
round
有n个点和若干条通讯线路。初始时,所有据点均无归属。Alice执先手,双方轮流决策,每次可以选择占领地图上的某个无主据点。当n个据点均被占领后进行评定(先手多进行一轮也是合法的),若某条通讯线路两端的据点均被一方所占领,则这条通讯线路也视为被其占领。每方的通讯能力视为其占领的通讯线的通讯能力之和,Alice希望最大化Alice与Bob的通讯能力的差值,Bob则希望最小化这个值。假设双方均取最优策略,那么对于给定的地图这个差值是确定的。
要求兹磁q次操作,每次加入一条指定权值的边和删除边。强制在线。
1<=n,q<=100000。
考虑我们对于一个点i,用val[i]表示相连边的权值和。设先手占有的点val和为first,后手点val和为second,那么就是要最大化(first-second)/2(如果同一条边两端在两人手里就会抵消,否则算两次)
那么我们按val排序,每次两人就会选val最大的点,那么就是奇数项加进first,偶数项加进second。
我们拿棵splay维护下就行了。
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first #define SZ 666666 int ch[SZ][2],val[SZ],fa[SZ],n,q,o,an=0,root,siz[SZ]; ll gs[SZ]; void upd(int x) { if(!x) return; siz[x]=siz[ch[x][0]]+siz[ch[x][1]]+1; gs[x]=gs[ch[x][0]]; if(siz[ch[x][0]]&1) gs[x]+=-val[x]+gs[ch[x][1]]; else gs[x]+=val[x]-gs[ch[x][1]]; } void rot(int x) { int y=fa[x],p=ch[y][0]==x; int f=fa[y]; fa[x]=f; fa[y]=x; if(f) ch[f][ch[f][1]==y]=x; int z=ch[x][p]; ch[y][!p]=z; if(z) fa[z]=y; ch[x][p]=y; upd(y); upd(x); upd(f); } void splay(int x,int f=0) { while(fa[x]!=f) { int y=fa[x],z=fa[fa[x]]; if(z!=f) { if(ch[y][0]==x^ch[z][0]==y) rot(x); else rot(y); } rot(x); } if(!f) root=x; } void ins(int x) { int cur=root,lst; while(cur) { lst=cur; cur=ch[cur][val[cur]<x]; } int p=++an; ch[lst][val[lst]<x]=p; val[p]=x; fa[p]=lst; upd(p); upd(lst); splay(p); } void del(int x) { int cur=root; while(val[cur]!=x) cur=ch[cur][val[cur]<x]; splay(cur); if(ch[cur][0]*ch[cur][1]==0) { int s=ch[cur][0]^ch[cur][1]; fa[s]=0; root=s; } else { int p=ch[cur][1]; while(ch[p][0]) p=ch[p][0]; ch[p][0]=ch[cur][0]; fa[ch[p][0]]=p; fa[ch[cur][1]]=0; splay(ch[cur][0]); } } void init() { root=an=1; val[root]=0; } void dfs(int x=root,int d=0) { if(!x) return; dfs(ch[x][0],d+1); for(int i=1;i<=d;i++) putchar(' '); cout<<x<<": "<<val[x]<<"\n"; dfs(ch[x][1],d+1); } #define gc (getchar()) inline const ll& rll(ll& x) { ll tmp=0; bool fu=0; char s; while(s=gc,s!='-'&&(s<'0'||s>'9')) ; if(s=='-') fu=1; else tmp=s-'0'; while(s=gc,s>='0'&&s<='9') tmp=tmp*10+s-'0'; if(fu) return x=-tmp; else return x=tmp; } inline ll _gll() {ll p; rll(p); return p;} #define gll _gll() int vv[SZ],ea[SZ],eb[SZ],ec[SZ]; int main() { freopen("round.in","r",stdin); freopen("round.out","w",stdout); n=gll, q=gll, o=gll; //scanf("%d%d%d",&n,&q,&o); init(); for(int i=1;i<=n;i++) ins(0); ll lans=0; int cc=0; for(int i=1;i<=q;i++) { int a; scanf("%d",&a); if(a==1) { //ll x,y,z; //scanf("%I64d%I64d%I64d",&x,&y,&z); ll x=gll, y=gll, z=gll; x^=lans*o; y^=lans*o; if(x==y) { del(vv[x]); vv[x]+=z*2; ins(vv[x]); } else { del(vv[x]); del(vv[y]); vv[x]+=z; vv[y]+=z; ins(vv[x]); ins(vv[y]); } ++cc; ea[cc]=x; eb[cc]=y; ec[cc]=z; } else { ll p=gll; /*scanf("%I64d",&p);*/ p^=lans*o; int x=ea[p],y=eb[p],z=ec[p]; if(x==y) { del(vv[x]); vv[x]-=z*2; ins(vv[x]); } else { del(vv[x]); del(vv[y]); vv[x]-=z; vv[y]-=z; ins(vv[x]); ins(vv[y]); } } ll s=gs[root]; if(s<0) s=-s; s>>=1; printf("%I64d\n",lans=s); } }
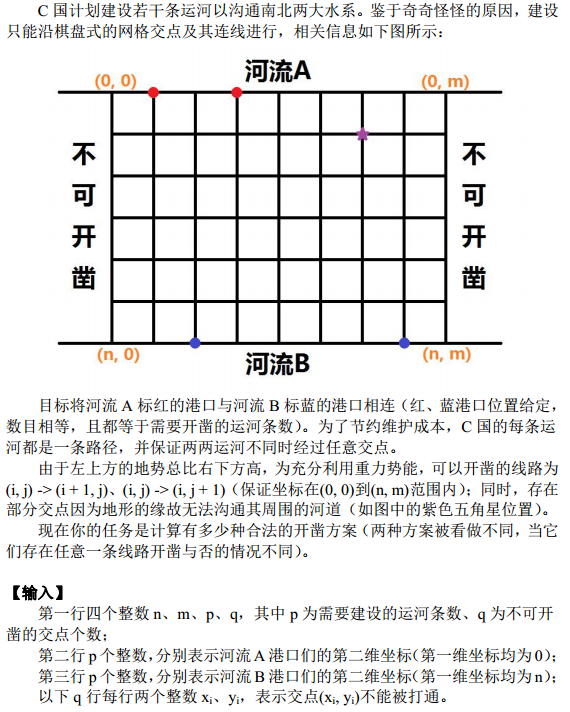
canal
题目这么长,自己看吧...
输出对998244353取模。
1<=n,m<=100000,1<=p,q<=200。
可以发现红点和蓝点排序后应该一一对应否则显然会交叉。
我们先来考虑每一对红蓝点之间的线路条数。
由于这是一张dag,我们可以把红、蓝、紫点拓扑排序(其实只要对于x坐标sort一下),然后统计一个点出发的红点,我们考虑dp,记f[i]为到第i个点中间不经过紫点的方案数,枚举不合法方案中第一个经过的紫点,则f[i]=g(红点,第i个点)-sum{f[j]*g(第j个点,第i个点)} (j为i前面的紫点)
接下来就要用到黑科技啦!
根据这个 https://en.wikipedia.org/wiki/Lindstr%C3%B6m%E2%80%93Gessel%E2%80%93Viennot_lemma 奥妙重重的引理,我们只要把这样第i个红点到第j个红点的路径条数ways[i][j]写成这个矩阵ways,如果红点蓝点都是有序的(实际上逆序对为偶数就行了),那么这个矩阵的行列式就是答案。
高斯消元一发即可。
需要注意的是...这题卡常...所以下面这个代码似乎过不去
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first #define SZ 666666 int n,m,p,q; int as[SZ],bs[SZ]; int MOD=998244353; int xs[SZ],ys[SZ]; ll fac[SZ],rfac[SZ]; inline ll qp(ll a,ll b) { ll ans=1; while(b) { if(b&1) ans=ans*a%MOD; a=a*a%MOD; b>>=1; } return ans; } inline ll C(ll a,ll b) { return fac[a]*rfac[b]%MOD*rfac[a-b]%MOD; } pii obs[SZ]; ll dp[SZ]; inline ll ws(int dx,int dy) { if(dx<0||dy<0) return 0; return C(dx+dy,dx); } ll mat[233][233]; ll gauss() { for(int i=1;i<=p;i++) { int tat=-1; for(int j=i;j<=p;j++) { if(mat[j][i]) {tat=j; break;} } if(tat==-1) return 0; for(int j=1;j<=p;j++) swap(mat[i][j],mat[tat][j]); for(int j=i+1;j<=p;j++) { ll mul=mat[j][i]*qp(mat[i][i],MOD-2)%MOD; for(int k=1;k<=p;k++) mat[j][k]=(mat[j][k]-mat[i][k]*mul%MOD)%MOD; } } ll ans=1; for(int i=1;i<=p;i++) ans=ans*mat[i][i]%MOD; ans=(ans%MOD+MOD)%MOD; return ans; } #define ffi fi.fi #define fse fi.se inline void gans(int s) { int y=as[s]; for(int i=1;i<=q;i++) { dp[i]=ws(obs[i].fi,obs[i].se-y); for(int j=1;j<i;j++) dp[i]-=dp[j]*ws(obs[i].fi-obs[j].fi,obs[i].se-obs[j].se)%MOD; dp[i]=(dp[i]%MOD+MOD)%MOD; } for(int i=1;i<=p;i++) { ll ans=ws(n,bs[i]-y); for(int j=1;j<=q;j++) ans-=dp[j]*ws(n-obs[j].fi,bs[i]-obs[j].se)%MOD; ans=(ans%MOD+MOD)%MOD; mat[s][i]=ans; } } int main() { freopen("canal.in","r",stdin); freopen("canal.out","w",stdout); fac[0]=rfac[0]=1; for(int i=1;i<=200000;i++) fac[i]=fac[i-1]*i%MOD; for(int i=1;i<=200000;i++) rfac[i]=rfac[i-1]*qp(i,MOD-2)%MOD; scanf("%d%d%d%d",&n,&m,&p,&q); for(int i=1;i<=p;i++) scanf("%d",as+i); for(int i=1;i<=p;i++) scanf("%d",bs+i); for(int i=1;i<=q;i++) scanf("%d%d",xs+i,ys+i); for(int i=1;i<=q;i++) obs[i]=pii(xs[i],ys[i]); sort(as+1,as+1+p); sort(bs+1,bs+1+p); sort(obs+1,obs+1+q); for(int i=1;i<=p;i++) gans(i); cout<<gauss()<<"\n"; }
这篇就写到这里...大概就是前几天每场写了两题...




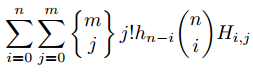
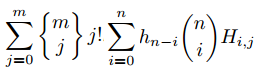








 浙公网安备 33010602011771号
浙公网安备 33010602011771号