APIO2013 tasksauthor
喜闻乐见的提答题,这道题还是蛮有趣的
数据结构题写得心塞,来一道提答意思意思
如果喜欢这类题的话还可以去做做uoj83。
这题是给出了两个问题,一个最短路,一个无向图染色问题。
Data 1
Floyd VS Dijkstra
嗯107个整数,我们只要给一个n=101,下面一坨0 Floyd就狗带了
#include <iostream> #include <stdio.h> using namespace std; int main() { printf("101\n"); for(int i=1;i<=101;i++) puts("0"); puts("1"); printf("%d %d\n",0,100); }
Data 2
啥Floyd 艹 Bellman-Ford?
看了一下代码…似乎真的可以随便艹掉。
Floyd:O(n^3),询问O(1)。
Bellman-Ford:询问O(ne)。
似乎随机数据一波就行?然而随机数据烂了。
这个点就是想让我们得到一个让bellman-ford和理论复杂度相差无几的数据。
其实很简单啊…加一坨没用的自环,然后剩下的搞一个5->4->3->2->1这样的链即可。
#include <iostream> #include <stdio.h> using namespace std; int main() { puts("100"); int mm=950; for(int i=0;i<100;i++) { int mx=min(mm,15),mxx=mx; mm-=mx; if(i!=0) ++mx; printf("%d",mx); if(i!=0) printf(" %d 2333",i-1); for(int j=1;j<=mxx;j++) printf(" %d 2333",i); putchar(10); } puts("10"); for(int i=1;i<=10;i++) printf("99 0\n"); }
Data 3
Bellman-Ford vs Floyd
用data 1即可
Data 4
Floyd 艹 Dijkstra!限制157个数!
咦似乎文件名叫“ModifiedDijkstra”看起来非常厉害
看了一下代码似乎没什么问题
咦可以有负权边…
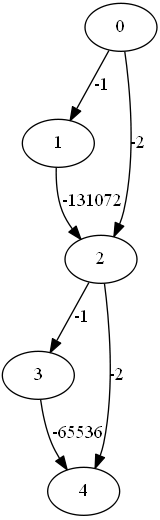
怎么搞呢?如图所示。
这里的更新顺序会变成0,2,4,3,4,1,2,4,3,4,这样再接上去几个就成了指数级啦
#include <iostream> #include <stdio.h> using namespace std; int main() { int bs=3*(1<<17),n=33; //可能要调一下 printf("%d\n",n); for(int i=0;i<n;i++) { if(i==n-1) {puts("0"); continue;} else if(i&1) printf("1 %d %d\n",i+1,-(bs/=2)); else printf("2 %d %d %d %d\n",i+1,-1,i+2,-2); } puts("6"); for(int i=1;i<=6;i++) printf("0 %d\n",n-1); }
UPD:这道题的改进版出现在IPSC2015 D,大家可以试做一下。
Data 5
Dijkstra 艹 Bellman-Ford
需要把Data 2稍加优化(人肉二分)
#include <iostream> #include <stdio.h> using namespace std; int main() { int N=300; int cnt=0; printf("%d\n",N), cnt++; int mm=40; for(int i=0;i<N;i++) { int mx=min(mm,15),mxx=mx; mm-=mx; if(i!=0) ++mx; printf("%d",mx), cnt++; if(i!=0) printf(" %d 2333",i-1), cnt+=2; for(int j=1;j<=mxx;j++) printf(" %d 2333",i), cnt+=2; putchar(10); } puts("10"), ++cnt; for(int i=1;i<=10;i++) printf("%d 0\n",N-1), cnt+=2; cerr<<"cnt="<<cnt<<"\n"; }
Data 6
Bellman-Ford 艹 Dijkstra
用Data 4即可。
Data 7
这回是一个平面图染色问题。
我们发现Gamble1是不会T的,现在我们就要让RecursiveBacktracking T掉。
我随机生成了个树,随机加了一坨边,就T了。
#include <iostream> #include <stdio.h> #include <map> using namespace std; map<int,bool> ms[105]; int main() { int n=100,m=1501; printf("%d %d\n",n,m); for(int i=1;i<n;i++) { int p=rand()%i; printf("%d %d\n",i,p), --m; ms[i][p]=ms[p][i]; } while(m) { int a=rand()%n,b=rand()%n; if(ms[a][b]||a==b) continue; printf("%d %d\n",a,b); ms[a][b]=ms[b][a]=1; --m; } }
Data 8
要让RecursiveBacktracking A掉而且数据范围有下限
随便搞啦
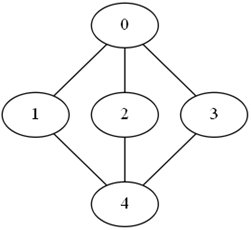
这份代码生成粗来类似这样
随手加了一点重边什么的
#include <iostream> #include <stdio.h> #include <map> using namespace std; map<int,bool> ms[1005]; #define BS 4 int main() { int n=996/BS*BS+1,m=1501; printf("%d %d\n",n,m); for(;;) { for(int i=0;i<n;i++) { if(i==n-1) continue; if(i%BS==0) { for(int j=1;j<BS;j++) { --m; printf("%d %d\n",i,i+j); if(!m) exit(0); } } else { --m; printf("%d %d\n",i,(i/BS+1)*BS); if(!m) exit(0); } } } }
感觉这道题答出的还行,大概做了2h的样子


 浙公网安备 33010602011771号
浙公网安备 33010602011771号