莫比乌斯反演2

bzoj3529 数表

令F(i)为i的约数和，q次给定n,m,a，求

$\sum_{\substack{1 \leq i \leq n\\1 \leq j \leq m\\F(gcd(i,j) \leq a}}{F(gcd(i,j))}{mod2^{31}}$

n,m<=10^5，q<=20000，a<=10^9(然而并没有什么卵用

对于这类题，我们先不管a好了。

由之前的某道题我们可以知道，假设g(i)为1<=x<=n,1<=y<=m,gcd(x,y)=i的(x,y)个数。

则$g(i)=\sum_{i|d}{\mu(\frac{d}{i})\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor}$ 。

线筛可以求出f(i)。

那么$ans=\sum _{i=1}^{min(n,m)} {F(i)g(i)}=\sum _{i=1}^{min(n,m)} {F(i)\sum_{i|d} {\mu(\frac{d}{i})\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor}=\sum _{d=1}^{min(n,m)}{\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor}}{\sum_{i|d}F(i)\mu(\frac{d}{i})}$

我们可以发现我们只要把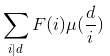 对于每一个i更新它的倍数算一下前缀和按照之前反演的方法搞搞即可。

那么a的限制怎么办呢？我们可以把所有询问按a排序，那么有贡献的就是F(i)<=a的。

把所有F(i)也排序之后暴力更新用树状数组维护一下前缀和就可以了。

mod 2^31的话由于某些原因只要用随便一种整数类型存一下然后对(2^31-1)and一下即可。

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
#include <string.h>
#include <vector>
#include <math.h>
#include <limits>
#include <set>
#include <map>
using namespace std;
#define S 233333
#define SZ 333333
typedef pair<int,int> pii;
int F[SZ],lst[SZ],cp[SZ],bits[SZ],tp[SZ],ps[SZ],pn=0,mu[SZ];
bool np[SZ];
void add(int x,int y)
{
    for(;x<=S;x+=x&-x) bits[x]+=y;
}
int sum(int x)
{
    int ans=0;
    for(;x>=1;x-=x&-x) ans+=bits[x];
    return ans;
}
void xs()
{
    F[1]=mu[1]=1;
    for(int i=2;i<=S;i++)
    {
        if(!np[i]) {F[i]=i+1; lst[i]=1; cp[i]=i; tp[i]=i+1; ps[++pn]=i; mu[i]=-1;}
        for(int j=1;j<=pn&&ps[j]*i<=S;j++)
        {
            np[i*ps[j]]=1;
            if(i%ps[j])
            {
                F[i*ps[j]]=F[i]*(ps[j]+1);
                lst[i*ps[j]]=i; cp[i*ps[j]]=ps[j];
                tp[i*ps[j]]=ps[j]+1;
                mu[i*ps[j]]=-mu[i];
            }
            else
            {
                lst[i*ps[j]]=lst[i];
                cp[i*ps[j]]=cp[i]*ps[j];
                tp[i*ps[j]]=tp[i]+cp[i*ps[j]];
                F[i*ps[j]]=F[lst[i]]*(tp[i*ps[j]]);
                mu[i*ps[j]]=0; break;
            }
        }
    }
}
struct xs_init{xs_init(){xs();}}_xs;
pii fs[SZ];
struct Q {int n,m,a,id;}qs[SZ];
int q,qans[SZ];
bool operator < (Q a,Q b) {return a.a<b.a;}
void upd(int x)
{
    for(int d=x;d<=S;d+=x) add(d,F[x]*mu[d/x]);
}
void sol()
{
    scanf("%d",&q);
    for(int i=1;i<=q;i++)
        scanf("%d%d%d",&qs[i].n,&qs[i].m,&qs[i].a), qs[i].id=i;
    sort(qs+1,qs+1+q);
    int fc=1;
    for(int i=1;i<=S;i++) bits[i]=0;
    for(int i=1;i<=q;i++)
    {
        while(fc<=S&&fs[fc].first<=qs[i].a) upd(fs[fc++].second);
        int lst,ans=0,N=qs[i].n,M=qs[i].m;
        for(int i=1;i<=N&&i<=M;i=lst+1)
        {
            lst=min(N/(N/i),M/(M/i));
            ans+=(N/i)*(M/i)*(sum(lst)-sum(i-1));
        }
        qans[qs[i].id]=ans&2147483647;
    }
    for(int i=1;i<=q;i++) printf("%d\n",qans[i]);
}
int main()
{
    for(int i=1;i<=S;i++) fs[i]=pii(F[i],i);
    sort(fs+1,fs+1+S); sol();
}