计算几何初步
嗯因为本人就是个计算几何渣所以标题就写个初步好了…
①求多边形面积 poj3907
随便找一个点,对多边形相邻顶点求叉积。加在一起求绝对值即可。
#include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <vector> #include <math.h> #include <limits> #include <set> #include <map> using namespace std; int n; double x[2333333],y[2333333]; int main() { while(scanf("%d",&n),n) { for(int i=0;i<n;i++) scanf("%lf%lf",x+i,y+i); double mx=2000000000,my=2000000000; for(int i=0;i<n;i++) mx=min(mx,x[i]), my=min(my,y[i]); --mx; --my; double ans=0; for(int i=0;i<n;i++) { double x1=x[i]-mx, y1=y[i]-my; double x2=x[(i+1)%n]-mx, y2=y[(i+1)%n]-my; ans+=x1*y2-y1*x2; } ans/=2; if(ans<0) ans=-ans; printf("%.0lf\n",ans); } }
②点是否在多边形内 zoj1081
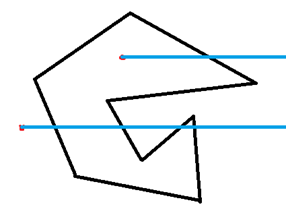
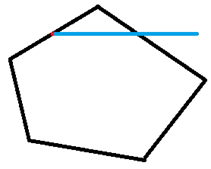
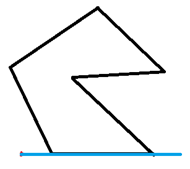
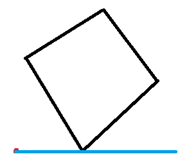
经典问题了,只要把这个点水平地做一条射线,然后统计经过多边形边的交点数。
经过一番严谨的推导(需要的自行百度),我们发现只要判一下和多边形交点的奇偶性就可以了。
听起来很简单…我连着WA了大概二十几发
边界:
在多边形边界上要特判
要忽略水平边
交点正好是多边形端点时判断另一个段点的上下(就是多边形的边在直线上面还是下面分别算0个或者1个交点,这样交在顶点上算两次就都是偶数)
写起来各种蛋疼,而且这题多组数据还有PE…醉了
#include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <vector> #include <math.h> #include <limits> #include <set> #include <map> using namespace std; typedef double ld; typedef pair<ld,ld> pnt; #define x first #define y second struct cl { ld a,b,c; cl() {a=b=c=0;} cl(ld A,ld B,ld C) {a=A;b=B;c=C;} }; int n,m; pnt as[233333]; ld eps=1e-6; cl gl(pnt a,pnt b) { return cl(a.y-b.y,b.x-a.x,a.x*b.y-a.y*b.x); } bool zero(ld s) {return fabs(s)<eps;} bool oncl(cl a,pnt b) { return zero(a.a*b.x+a.b*b.y+a.c); } bool onseg(pnt a,pnt b,pnt c) { if(!oncl(gl(a,b),c)) return 0; if(min(a.x,b.x)-eps<=c.x&&c.x<=max(a.x,b.x)+eps);else return 0; if(min(a.y,b.y)-eps<=c.y&&c.y<=max(a.y,b.y)+eps);else return 0; return 1; } bool same(pnt a,pnt b) { return zero(a.x-b.x)&&zero(a.y-b.y); } bool chk(pnt s) { //在多边形边上 for(int i=0;i<n;i++) { if(onseg(as[i],as[(i+1)%n],s)||same(as[i],s)) return 1; } int cnt=0; for(int i=0;i<n;i++) { //水平线不考虑 if(zero(as[i].y-as[(i+1)%n].y)) continue; cl cll=gl(as[i],as[(i+1)%n]); ld xx=(-cll.b*s.y-cll.c)/cll.a,yy=s.y; //交点 if(!onseg(as[i],as[(i+1)%n],pnt(xx,yy))||xx<s.x) continue; if(same(pnt(xx,yy),as[i])||same(pnt(xx,yy),as[(i+1)%n])) { if(same(pnt(xx,yy),as[i])) cnt+=as[(i+1)%n].y>yy; else cnt+=as[i%n].y>yy; } else cnt++; } return cnt&1; } void ip(pnt& s) { scanf("%lf%lf",&s.x,&s.y); } int main() { int T=0,fst=1; while(scanf("%d",&n),n) { ++T; scanf("%d",&m); for(int i=0;i<n;i++) ip(as[i]); if(!fst) puts(""); else fst=0; printf("Problem %d:\n",T); for(int i=0;i<m;i++) { pnt cur; ip(cur); if(chk(cur)) puts("Within"); else puts("Outside"); } } }
③凸包&旋转卡(qiǎ)壳(qiào) poj2187
其实这题不用旋转卡壳也能过,因为坐标为[0,N]整点的凸包顶点个数是不超过$\sqrt{n}$的(当然如果不去除共线的话比较玄学)。
没有旋转卡壳:
#include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <vector> #include <math.h> #include <limits> #include <set> #include <map> using namespace std; typedef double ld; typedef pair<ld,ld> pnt; #define X first #define Y second int n; pnt yd,a[233333]; ld eps=1e-6; bool cmp1(pnt a,pnt b) { if(fabs(a.Y-b.Y)>1e-6) return a.Y<b.Y; else return a.X<b.X; } bool cmp2(pnt a,pnt b) {return atan2(a.Y-yd.Y,a.X-yd.X)<atan2(b.Y-yd.Y,b.X-yd.X);} int st[233333],sn=0; ld cc(pnt a,pnt b,pnt c) { return (a.X-c.X)*(b.Y-c.Y)-(a.Y-c.Y)*(b.X-c.X); } ld dis(pnt a,pnt b) { return (a.X-b.X)*(a.X-b.X)+(a.Y-b.Y)*(a.Y-b.Y); } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%lf%lf",&a[i].X,&a[i].Y); sort(a+1,a+1+n,cmp1); yd=a[1]; sort(a+2,a+1+n,cmp2); for(int i=1;i<=3;i++) st[++sn]=i; for(int i=4;i<=n;i++) { while(sn>1&&cc(a[i],a[st[sn]],a[st[sn-1]])>=0) --sn; st[++sn]=i; } double maxx=0; for(int i=1;i<=sn;i++) { for(int j=i;j<=sn;j++) maxx=max(maxx,dis(a[st[i]],a[st[j]])); } printf("%.0lf\n",maxx); }
旋转卡壳:
#include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <vector> #include <math.h> #include <limits> #include <set> #include <map> using namespace std; typedef double ld; typedef pair<ld,ld> pnt; #define X first #define Y second int n; pnt yd,a[233333]; ld eps=1e-6; bool cmp1(pnt a,pnt b) { if(fabs(a.Y-b.Y)>1e-6) return a.Y<b.Y; else return a.X<b.X; } bool cmp2(pnt a,pnt b) {return atan2(a.Y-yd.Y,a.X-yd.X)<atan2(b.Y-yd.Y,b.X-yd.X);} int st[233333],sn=0; ld cc(pnt a,pnt b,pnt c) { return (a.X-c.X)*(b.Y-c.Y)-(a.Y-c.Y)*(b.X-c.X); } ld dis(pnt a,pnt b) { return (a.X-b.X)*(a.X-b.X)+(a.Y-b.Y)*(a.Y-b.Y); } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%lf%lf",&a[i].X,&a[i].Y); sort(a+1,a+1+n,cmp1); yd=a[1]; sort(a+2,a+1+n,cmp2); for(int i=1;i<=3;i++) st[++sn]=i; for(int i=4;i<=n;i++) { while(sn>1&&cc(a[i],a[st[sn]],a[st[sn-1]])>=0) --sn; st[++sn]=i; } double maxx=0; int cur=1; for(int i=1;i<=sn;i++) { while(fabs(cc(a[st[cur%sn+1]],a[st[i%sn+1]],a[st[i]]))>fabs(cc(a[st[cur]],a[st[i%sn+1]],a[st[i]]))) cur=cur%sn+1; maxx=max(maxx,dis(a[st[cur]],a[st[i]])); maxx=max(maxx,dis(a[st[cur]],a[st[i%sn+1]])); } printf("%.0lf\n",maxx); }