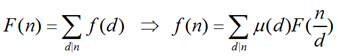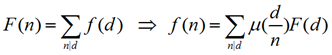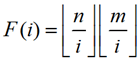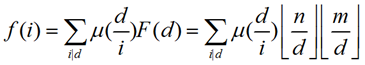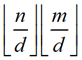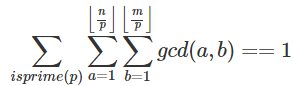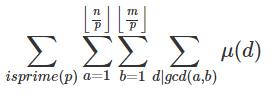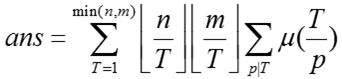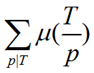莫比乌斯反演
友情提醒：这篇文章中的大部分东西都出自popoqqq的课件《莫比乌斯反演》和hzwer的博客，orz
首先我们来看一个函数，$F(n)=\sum_{d|n}{f(d)}$。
这个函数还是十分常见的。例如我们令f(d)=d，那么F(n)就可以表示n的因数和。
那么
F(1)=f(1)
F(2)=f(1)+f(2)
F(3)=f(1)+f(3)
F(4)=f(1)+f(2)+f(4)
F(5)=f(1)+f(5)
F(6)=f(1)+f(2)+f(3)+f(6)
F(7)=f(1)+f(7)
F(8)=f(1)+f(2)+f(4)+f(8)
于是我们可以用F反推出f。
f(1)=F(1)
f(2)=F(2)-F(1)
f(3)=F(3)-F(1)
f(4)=F(4)-F(2)
f(5)=F(5)-F(1)
f(6)=F(6)-F(3)-F(2)+F(1)
f(7)=F(7)-F(1)
f(8)=F(8)-F(4)
咦我似乎看出了一些非常厉害的东西…
我们来定义一个函数$\mu$，我们发现我们可以找到这样的一个函数使得
$f(n)=\sum_{d|n} \mu(d) F(\frac{n}{d})$
我们根据上面的那些式子容易看出μ(1)=1，μ(2)=-1，μ(3)=-1，μ(4)=0，μ(5)=-1，μ(6)=1，μ(7)=-1，μ(8)=0…
估计正常人都看不出来μ是啥吧…
μ(x)定义如下：
若x=1则μ(x)=1。
若$x=p_1p_2p_3...p_k$，p为互异素数，那么μ(x)=(-1)^k。
其它情况下μ(x)=0。
这个函数有一些性质，首先$\sum_{d|n} \mu(d)=[n=1]$。
其次这玩意儿是积性函数，即对于互质的两个数a，b，μ(ab)=μ(a)μ(b)，所以我们可以线筛筛出这个函数，具体过程和筛phi差不多。
//筛miu bool np[SZ]; int ps[SZ],pn=0; void gp() { mu[1]=1; for(int i=2;i<=200000;i++) { if(!np[i]) ps[++pn]=i, mu[i]=-1; for(int j=1;ps[j]*i<=200000&&j<=pn;j++) { np[ps[j]*i]=1; if(i%ps[j]) mu[ps[j]*i]=-mu[i]; else {mu[ps[j]*i]=0; break;} } } }
第三
这个过程叫做莫比乌斯反演。
那么这有什么用呢？比如如果F比较好求而我们要求f，我们就可以用这个反演来简化。
我们来看点例题好了。
bzoj2301 Problem b
q次询问，每次询问有多少个数对(x,y)满足a<=x<=b,c<=y<=d且gcd(x,y)=k
q<=50000，1<=a<=b<=50000，1<=c<=d<=50000。
首先我们可以发现我们只要能求1<=x<=n，1<=y<=m且gcd(x,y)=k的数量即可，因为我们可以容斥原理大法好。
由于莫比乌斯反演，我们可以令f(i)为1<=x<=n，1<=y<=m且gcd(x,y)=i的(x,y)的个数，F(i)为1<=x<=n，1<=y<=m且i|gcd(x,y)的(x,y)的个数
那么明显
。
反演一下
所以我们可以在O(n)的时间内解决每个询问啦！
咦好像还是太慢了…
我们发现
最多有
个取值
所以我们枚举
的
个取值，然后维护一个μ的前缀和就可以啦！
啥怎么写？
//bzoj2301 #include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <vector> #include <limits> #include <set> #include <map> using namespace std; #define SZ 233333 int n,a,b,c,d,k,mu[SZ],qzh[SZ]; namespace g_p { bool np[SZ]; int ps[SZ],pn=0; void gp() { mu[1]=1; for(int i=2;i<=200000;i++) { if(!np[i]) ps[++pn]=i, mu[i]=-1; for(int j=1;ps[j]*i<=200000&&j<=pn;j++) { np[ps[j]*i]=1; if(i%ps[j]) mu[ps[j]*i]=-mu[i]; else {mu[ps[j]*i]=0; break;} } } for(int i=1;i<=200000;i++) qzh[i]=qzh[i-1]+mu[i]; } } long long query(int n,int m,int k) { n/=k; m/=k; int lst; long long ans=0; for(int i=1;i<=n&&i<=m;i=lst+1) { lst=min(n/(n/i),m/(m/i)); ans+=(long long)(n/i)*(m/i)*(qzh[lst]-qzh[i-1]); } return ans; } int main() { g_p::gp(); scanf("%d",&n); while(n--) { int a,b,c,d,k; scanf("%d%d%d%d%d",&a,&c,&b,&d,&k); printf("%lld\n",query(c,d,k)-query(a-1,d,k)-query(c,b-1,k)+query(a-1,b-1,k)); } }
bzoj2820 YY的GCD
求1<=x<=N，1<=y<=M且gcd(x, y)为质数的(x, y)有多少对。多组询问，T<=10000，N,M<=10000000。
即
由上面莫比乌斯函数的第一个性质可以得到
原式即
也即$\sum_{isprime(p)}\sum_{a=1}^{\left\lfloor\frac{n}{p}\right\rfloor}\sum_{b=1}^{\left\lfloor\frac{m}{p}\right\rfloor}\sum_{d|a\&d|b}\mu(d)$
那么也就是
令pd=T，那么有
套用和上一题一样的方法，那现在问题就是要求出
的前缀和
于是我们暴力枚举每一个质数即可！
为什么呢？因为质数的个数是大约n/lnn，然后众所周知$\sum_{i=1}^n{\frac{1}{i}}$是趋近于lnn的。
那么$\sum_{i=1}^n{\frac{n}{i}}$趋近于nlnn，所以平均到n个数每一个数均摊是lnn的，所以因为质数是均匀分布的，所以平均每个质数更新大约也是lnn的，然后一共n/lnn个质数，复杂度据说就差不多是O(n)的了。
//bzoj2820 #include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <vector> #include <limits> #include <set> #include <map> using namespace std; #define SZ 23333333 int n,a,b,c,d,k,mu[SZ]; long long qzh[SZ]; namespace g_p { bool np[SZ]; int ps[SZ],pn=0; #define MAXN 10000000 void gp() { mu[1]=1; for(int i=2;i<=MAXN;i++) { if(!np[i]) ps[++pn]=i, mu[i]=-1; for(int j=1;ps[j]*i<=MAXN&&j<=pn;j++) { np[ps[j]*i]=1; if(i%ps[j]) mu[ps[j]*i]=-mu[i]; else {mu[ps[j]*i]=0; break;} } } for(int i=1;i<=pn;i++) { int p=ps[i]; for(int j=1;j*p<=MAXN;j++) qzh[p*j]+=mu[j]; } for(int i=1;i<=MAXN;i++) qzh[i]+=qzh[i-1]; } } long long query(int n,int m) { int lst; long long ans=0; for(int i=1;i<=n&&i<=m;i=lst+1) { lst=min(n/(n/i),m/(m/i)); ans+=(long long)(n/i)*(m/i)*(qzh[lst]-qzh[i-1]); } return ans; } int main() { g_p::gp(); scanf("%d",&n); while(n--) { int a,b; scanf("%d%d",&a,&b); printf("%lld\n",query(a,b)); } }
