线段树-初识

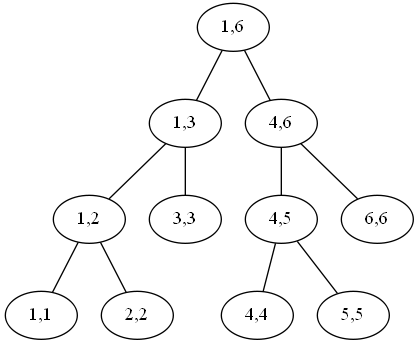
线段树嘛…就是一个长得像这个样子的一棵树！

这颗树上的一个点就代表了一个连续的区间，当然如果你高兴也可以把区间当成线段，所以这玩意儿就叫线段树。然后我们发现一个点的左孩子右孩子就是把这个区间从中间剖成两段后的前一段后一段。

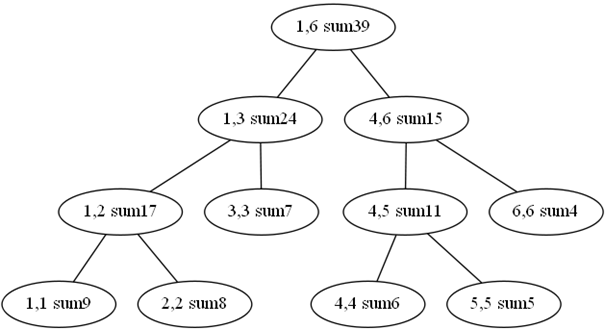
比如我们现在有一个数列…就9 8 7 6 5 4好了

那我们可以在线段树上维护一个这个区间内元素的和，我们发现，左端点=右端点的这些点的和就是数列里的元素，如果不等于，和就等于左孩子的和+右孩子的和。

我们容易发现，对于一个长度为n的数列，树高的期望是O(logn)的。为什么呢？仔细想想你会发现这是废话，因为每一层区间都会短一半，当然期望就是log啦。

我们还会发现对于一个长度为n的数列，总共的点的数量是O(n)的。这好像不是废话。我们考虑n是2的次幂好了，这样每个区间就正好都是剖分成两半，比较好算。那我们设n=2^k，那么第一层有1个点，第二层有2个点，第三层有4个点，…，第n层有2^(n-1)个点，一共k+1层。那么总共也就是1+2+4+…+2^k=1+(1+2+4+…+2^k)-1=2^(k+1)-1=2n-1，所以也就差不多是O(n)啦。

拿上面的那个图为例好了，如果我们要问你[2,5]的和，要怎么查询呢？

呀你会发现图里面没有[2,5]，但是我们发现[2,5]可以割成若干段图里有的区间，我们可以把它割成[2,2] [3,3] [4,5]这三段。

我们发现如果我们从上面[1,6]开始考虑，我们可以这么想，我们知道左边是[1,3]，右边是[4,6]…

我们对于左边和右边分开考虑。落在左边的是[2,3]，落在右边的是[4,5]…

类似这样往下查询就可以查出来啦。

具体过程可以看下面…

对于[1,6]：我们发现要查询的是[2,5]，好像这个区间本身的信息不太够啊，于是查询左右孩子，发现落在左边[1,3]的是[2,3]，落在右边[4,6]的是[4,5]。

    对于[1,3]：我们发现要查询[2,3]信息还是不够。我们查询左右孩子，落在左边[1,2]的是[2,2]，落在右边[3,3]的是[3,3]。

        对于[1,2]：好像查[2,2]信息还是不够…我们查询左右孩子，发现左边[1,1]好像没什么关系，落在右边[2,2]的是[2,2]。

            对于[2,2]：呀好像我知道[2,2]和了，我区间上有记录，sum=8，[2,2]的和为8。

        对于[1,2]：哦那我也知道了[2,2]的和为8。

        对于[3,3]：要查询[3,3]？我区间上有记录，sum=7，[3,3]的和为7。

    对于[1,3]：哦[2,2]和为8，[3,3]和为7，那么[2,3]和为15。

    对于[4,6]：要查[4,5]…信息不够啊。左边[4,5]落在里面的是[4,5]，右边没啥关系。

        对于[4,5]：哦[4,5]我区间上有记录，[4,5]的和为11。

    对于[4,6]：好[4,5]的和为11。

对于[1,6]：[2,3]和为15，[4,5]和为11，看来[2,5]和就为26啊。

所以我相信如果你看懂了这段查询过程，你已经大概知道查询要怎么写了。

我们可以发现同一层的节点顶多会访问两个。（因为如果访问超过2个那么必定有两个不是黏在一起的。如果不是黏在一起的既然询问是连续的，肯定至少有一个可以往上一层走，从而减小了所需的询问区间数量，但这样分解区间数量显然是最优的）

所以因为层数是O(logn)的所以访问的节点数也是O(logn)的，所以这样查询是O(logn)的。

那么修改就更简单了，只要从修改的那个点往根走，边走边修改sum就行了。那么这样访问的节点数肯定也和层数一样是O(logn)的。至于修改的那个点怎么找…只要从根往左右走就行了。

这样写出来的线段树嘛…其实还挺好写的。

我个人线段树的码风比较奇怪……对于一个点x，左孩子是x+x，右孩子是x+x+1。

（据说加法比位移快，然而我并不信）

//codevs1080 区间求和 单点加一个数
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
#include <string.h>
#include <vector>
#include <limits>
#include <set>
#include <map>
using namespace std;
typedef long long ll;
int n,q;
ll sum[666666],a[666666];
void init(int c,int l,int r)
{
    if(l==r) {sum[c]=a[l]; return;}
    int mid=l+r>>1;
    init(c+c,l,mid);
    init(c+c+1,mid+1,r);
    sum[c]=sum[c+c]+sum[c+c+1];
}
ll gsum(int c,int l,int r,int ql,int qr)
{
    if(ql>qr) return 0;
    if(l==ql&&r==qr) return sum[c];
    int mid=l+r>>1; ll ans=0;
    ans+=gsum(c+c,l,mid,ql,min(qr,mid));
    ans+=gsum(c+c+1,mid+1,r,max(ql,mid+1),qr);
    return ans;
}
void edit(int c,int l,int r,int p,int v)
{
    if(l==r) {sum[c]+=v; return;}
    int mid=l+r>>1;
    if(p<=mid) edit(c+c,l,mid,p,v);
    else edit(c+c+1,mid+1,r,p,v);
    sum[c]=sum[c+c]+sum[c+c+1];
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%lld",a+i);
    init(1,1,n);
    scanf("%d",&q);
    while(q--)
    {
        int x,a,b;
        scanf("%d%d%d",&x,&a,&b);
        if(x==1) edit(1,1,n,a,b);
        else printf("%lld\n",gsum(1,1,n,a,b));
    }
}