6.15 工程数学实验二
实验二：最速下降法程序设计
一、实验目的
通过最速下降法的程序设计，为今后的约束优化方法的学习和编程奠定基础；掌握负梯度方向的定义和最速下降法的迭代公式；通过此次实验，进一步巩固最速下降法的基本原理和思想。
二、实验内容
（1）求解无约束优化问题：；
（2）终止准则取；
（3）完成最速下降法（负梯度法）的MATLAB编程、调试；
（4）要求选取多个不同的初始点，并给出迭代次数，最优函数值等相关信息，有能力的同学尝试画出最优值随迭代次数变化的曲线图；
（5）按照模板撰写实验报告，要求规范整洁。
三、算法步骤、代码、及结果
1. 算法步骤
首先定义实验的函数，然后算出梯度，给出几组例值。
2. 代码
% 定义目标函数
f = @(x) (x(1)+10*x(2))^2 + 5*(x(3)-x(4))^2+(x(2)-2*x(3)^4+10*(x(1)-x(4)))^2;
% 最速下降法求解
% 设定初始点和迭代终止准则
x0_list = [-2, 5, 6, 7; 2 ,2 ,6 , 5; 0.5, -1.5, 2, 5]; % 多个不同的初始点
max_iter = 10000;
tol = 1e-5;
results = zeros(size(x0_list, 1), 4); % 存储最优结果
for i = 1:size(x0_list, 1)
x0 = x0_list(i,:);
x = x0';
a = 0.01; % 步长
iter = 0;
grad_norm = inf;
func_values = zeros(max_iter, 1); % 新增：记录每一步的函数值
while grad_norm > tol && iter < max_iter
iter = iter + 1;
grad = [400*x(1)^3-400*x(1)*x(2)+2*x(1)-2;
200*(x(2)-x(1)^2);
10*(x(3)-x(4));
-10*(x(3)-x(4))];
x_new = x - a*grad;
if f(x_new) < f(x)
x = x_new;
a = a * 1.1;
else
a = a * 0.5;
end
grad_norm = norm(grad);
func_values(iter) = f(x); % 记录当前迭代的函数值
end
results(i, :) = x;
fprintf('初始点 (%g, %g, %g, %g)\n', x0(1), x0(2), x0(3), x0(4));
fprintf('迭代次数: %d\n', iter);
fprintf('最优点: (%g, %g, %g, %g)\n', x(1), x(2), x(3), x(4));
fprintf('最优函数值: %g\n', f(x));
fprintf('\n');
% 绘制当前初始点对应的函数值变化曲线
plot(1:iter, func_values(1:iter), 'LineWidth', 1.5, ...
'DisplayName', sprintf('初始点%d', i));
hold on;
end
% 添加标题、标签、图例和网格
xlabel('迭代次数');
ylabel('函数值');
title('函数值随迭代次数变化');
legend('show');
grid on;
hold off;
3. 结果
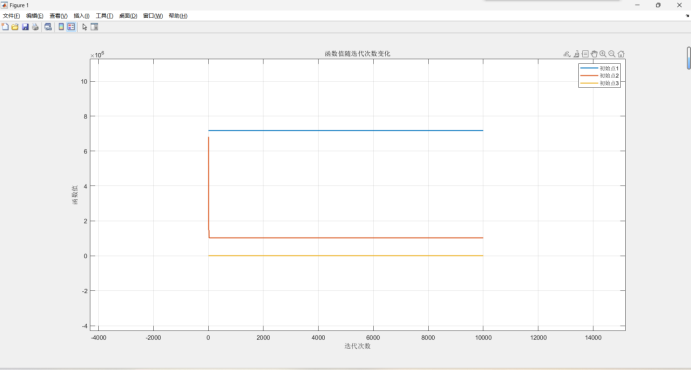
四、心得体会
在这个实验中，我学习了最速下降法的基本原理和实现过程。通过编程实践，我掌握了负梯度方向的定义和最速下降法的迭代公式。在实验中，我首先定义了目标函数，并计算了其梯度。然后，我选择了多个不同的初始点，并设置了迭代终止准则。在迭代过程中，我不断更新参数，直到满足了停止条件或达到最大迭代次数。
通过实验，我深入理解了最速下降法的迭代过程，以及如何根据梯度信息来更新参数以找到函数的局部最小值。我还学会了如何利用MATLAB编程语言来实现最速下降法，并且能够绘制出函数值随迭代次数变化的曲线图，以直观地观察算法的收敛情况。
总的来说，这个实验帮助我巩固了最速下降法的基本原理和思想，提高了我的编程能力和数值优化的实践经验。通过这次实验，我更加熟悉了优化算法的实现过程，并且对如何解决实际问题有了更深入的理解。
