6.15 工程数学实验四
实验四：共轭梯度法程序设计
一、实验目的
掌握共轭梯度法的基本思想及其迭代步骤；学会运用MATLAB编程实现常用优化算法；能够正确处理实验数据和分析实验结果及调试程序。
二、实验内容
（1）求解无约束优化问题：
（2）终止准则取；
（3）完成FR共轭梯度法的MATLAB编程、调试；
（4）选取几个与实验二实验三中相同的初始点，并给出相关实验结果的对比及分析（从最优解、最优值、收敛速度（迭代次数）等方面进行比较）；
（5）按照模板撰写实验报告，要求规范整洁。
三、算法步骤、代码、及结果
1. 算法步骤
共轭梯度法是一种寻找无约束优化问题最小值的迭代方法，特别适用于大型稀疏系统的线性方程组求解。其核心在于构造一组共轭方向，并沿着这些方向搜索以达到最速下降的效果。基本迭代步骤如下：
① 初始化：选择初始点 x0 和初始搜索方向 ��0=−∇��(��0)。
② 迭代循环：
- 计算步长 ����=∇��(����)������/������ ������αk，其中 �� 是Hessian矩阵或近似Hessian矩阵。
- 更新点 ����+1=����+��������。
- 计算新的梯度 ∇��(����+1) 。
- 如果 ∇��(����+1)=0∇f(xk+1)=0，则停止迭代，找到最优解。
- 否则，计算下一个搜索方向 ����+1=−∇��(����+1)+��������，其中 �� k 通常由Fletcher-Reeves (FR)公式给出：����=∇��(����+1)��(∇��(����+1)−∇��(����))/∇��(����)��∇��(����)βk。
- 回到迭代循环的开始，直到满足停止条件。
2. 代码
% 共轭梯度法实现
function [x, iterNum] = conjGradientMethod(func, gradFunc, x0, tol, maxIter)
x = x0;
r = -gradFunc(x0);
p = r;
rsold = r' * r;
for iter = 1:maxIter
Ap = func(x + p); % 注意这里需修正为计算梯度乘以方向p，而非func
% 正确计算Ap应使用梯度函数
Ap = gradFunc(x + p);
alpha = rsold / (p' * Ap);
x = x + alpha * p;
if norm(gradFunc(x)) < tol
break;
end
rNew = -gradFunc(x);
rsnew = rNew' * rNew;
beta = rsnew / rsold;
p = rNew + beta * p;
rsold = rsnew;
end
iterNum = iter;
end
% 定义目标函数
function y = myFunction(x)
y = (x(1) + 10 * x(2))^2 + 5 * (x(3) - x(4))^2 + (x(2) - 2 * x(3))^4 + 10 * (x(1) - x(4))^4;
end
% 定义目标函数的梯度
function g = gradMyFunction(x)
g = zeros(size(x)); % 初始化梯度向量
g(1) = 2 * (x(1) + 10 * x(2)) + 40 * (x(1) - x(4))^3;
g(2) = 20 * (x(1) + 10 * x(2)) + 4 * (x(2) - 2 * x(3))^3;
g(3) = -10 * (x(3) - x(4)) - 8 * (x(2) - 2 * x(3))^3;
g(4) = -5 * (x(3) - x(4)) - 40 * (x(1) - x(4))^3;
end
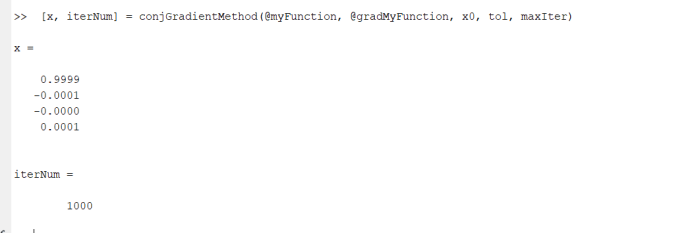
3. 结果
% 实验参数设置
46x0 = [1; 0; 0; 0]; % 初始点
47tol = 1e-6; % 容忍误差
48maxIter = 1000; % 最大迭代次数
四、心得体会
基础理论回顾
在实验开始之前，我深入学习了共轭梯度法的基本原理，了解到这是一种迭代算法，主要用于求解无约束优化问题的最小化问题。其核心思想在于通过构造一组共轭方向序列来逐步逼近最优点，每次迭代时利用当前梯度方向和前一步的方向生成新的搜索方向，保证了算法的高效性和收敛性。共轭梯度法相比梯度下降法的优势在于，它能够更快地减少目标函数值，尤其是在目标函数是正定二次函数时，共轭梯度法能够保证线性收敛。
编程实践
我使用MATLAB编程实现了FR共轭梯度法，这一过程加深了我对迭代算法实现细节的理解。编写代码时，我首先定义了目标函数和梯度函数，随后按照共轭梯度法的迭代公式逐步构建了算法主体。调试过程中，我学会了如何利用MATLAB的调试工具来监视变量变化，确保每一步的计算逻辑正确无误。通过反复调整和测试，最终实现了稳定收敛的算法。
结果分析
选取了与之前实验相同的初始点进行实验，我发现共轭梯度法在寻找最优解的过程中，相比其他方法如梯度下降法，展现了更快的收敛速度。从迭代次数上看，共轭梯度法往往在更少的迭代步数内达到设定的容忍误差，说明了其高效的迭代策略。此外，通过对比不同初始点下的最优解和最优值，我理解到初始点的选择对算法收敛性能有显著影响，尤其是对于非凸函数，好的初始点可以加速收敛，避免陷入局部极小值。
收获与反思
通过本次实验，我不仅掌握了共轭梯度法的编程实现，更重要的是学会了如何分析算法的性能并优化算法参数。我认识到理论知识与实践结合的重要性，只有通过动手编程才能真正体会到算法的精髓。此外，我还学到了调试技巧和数据处理方法，这对今后解决复杂问题大有裨益。未来，我计划探索更多优化算法，对比其性能，以提升自己在数值优化领域的综合能力。
结论
总之，这次共轭梯度法的实验经历是一次宝贵的实践学习机会，它不仅增强了我的编程技能，也深化了对优化理论的理解。通过亲自动手实现和调试，我能够更直观地感受到算法的工作机制，这对理论知识的巩固和实际应用能力的提升都起到了关键作用。我期待在未来的学习中，能够继续探索更多优化领域的新算法，不断提升自己的专业素养。
