c++打卡第三十天

一、阿姆斯特朗数

1、、问题描述

 2、设计思路

可以从1开始遍历，如果我们使用数组存储一个数的每位数，那么如此在位数不同的范围中需要不同长度的数组 ，如此过于繁琐，那么我们可以对一个数求余，对每个求余的立方数相加，然后对这个数除以10，直到这个数为0，然后将立方和得到的数与原数比较，如果数相同，那么这个数就是阿姆斯特朗数。

3、流程图

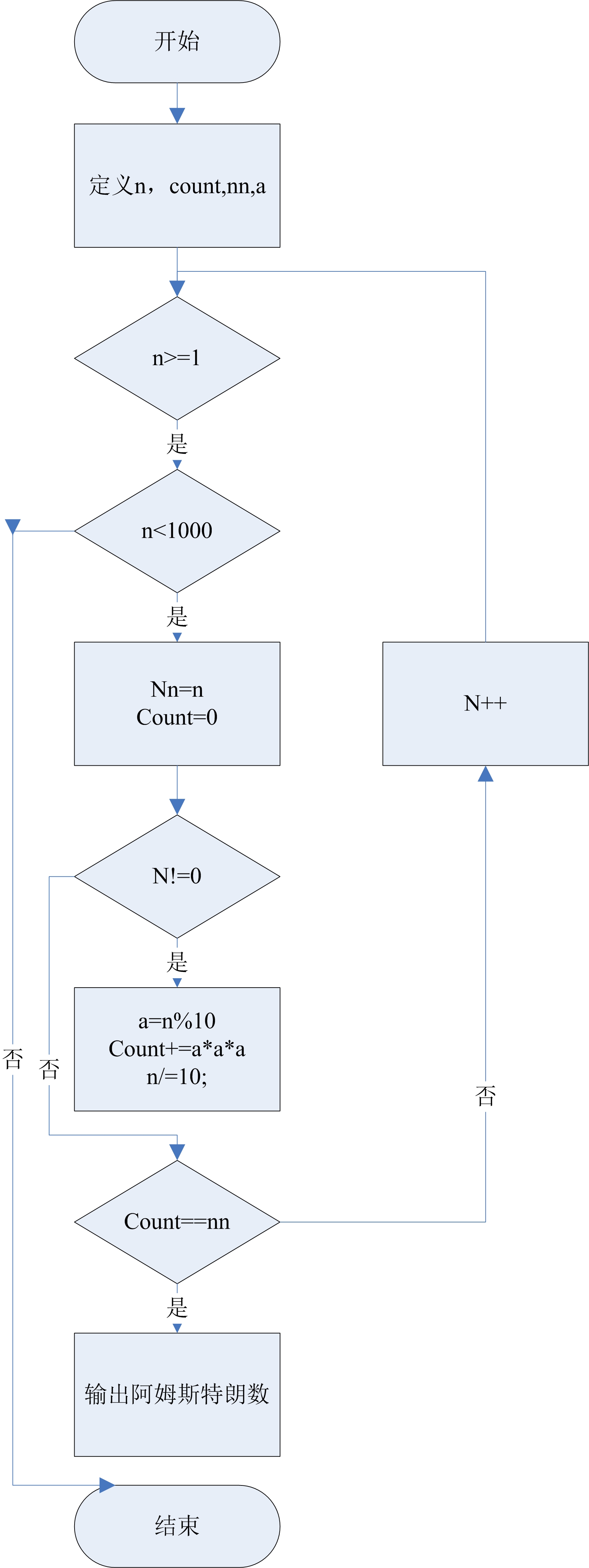
4、代码实现

#include<iostream>
using namespace std;
int main()
{
    long n,nn,a,count;
    for(n=1;n<1000;n++)
    {
        nn=n;
        count=0;
        while(nn!=0)
        {
            a=nn%10;
            count+=a*a*a;
            nn/=10;
        }
        if(count==n)
        {
            cout<<"阿姆斯特朗数为：   "<<n<<endl; 
        }
    }
    return 0;
 } 

5、结果实现

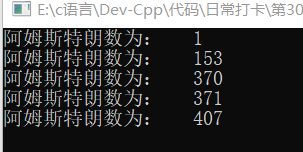
 二、高次方数的尾数

1、问题描述

 

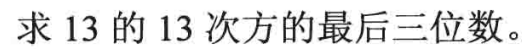
2、设计思路

我们这次求一个数的n次方的 最后n位数，我们可以发现，对于高位的乘法，不需要对其进行乘法运算，只需要所需要的最后几位数与这个数进行乘法运算。即last=last*x%pow（10，n）；

3、流程图

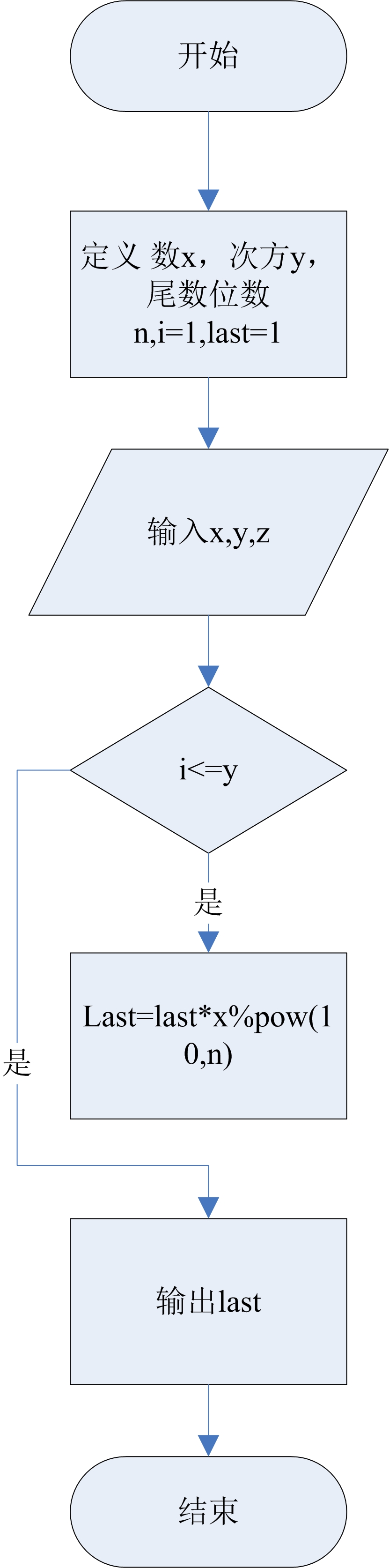
4、代码实现

#include<iostream>
#include<cmath>
using namespace std;
int main()
{
    int x,y,n,i=1,last=1;
    int flag=1;
    while(flag)
    {
        last=1;
        cin>>x;
        cin>>y;
        cin>>n;
        for(i=1;i<=y;i++)
        {
            int len=pow(10,n);
            last=(last*x)%len;
        }
        cout<<x<<"的"<<y<<"次方的"<<n<<"位尾数为："<<last<<endl; 
        cout<<"是否继续测试，是输入1 ，否输入0"<<endl;
        cin>>flag; 
    }
    return 0;
 } 

5、结果实现

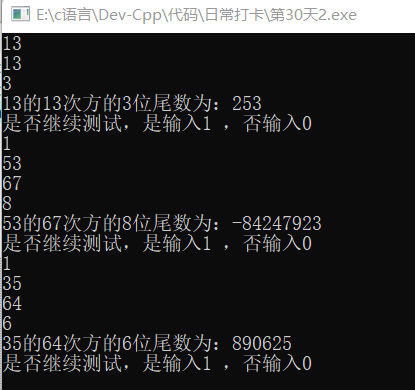
 6、该函数使用循环来计算的y次方的末x位。为了避免超出实数范围，我们使用模运算来保持结果的位数。在循环中，我们将累积乘积取模以防止溢出。最后，我们返回累积乘积的末x位。

#include <iostream>
#include <cmath>

using namespace std;

int powMod(int n, int y, int x) {
    int res = 1;
    for (int i = 0; i < y; i++) {
        res = res * n % (int) pow(10, x);
    }
    return res;
}

int main() {
    int n, y, x;
    cin >> n >> y >> x;
    cout << powMod(n, y, x) << endl;
    return 0;
}