c++打卡第二十六天
①
一、问题描述

二、设计思路
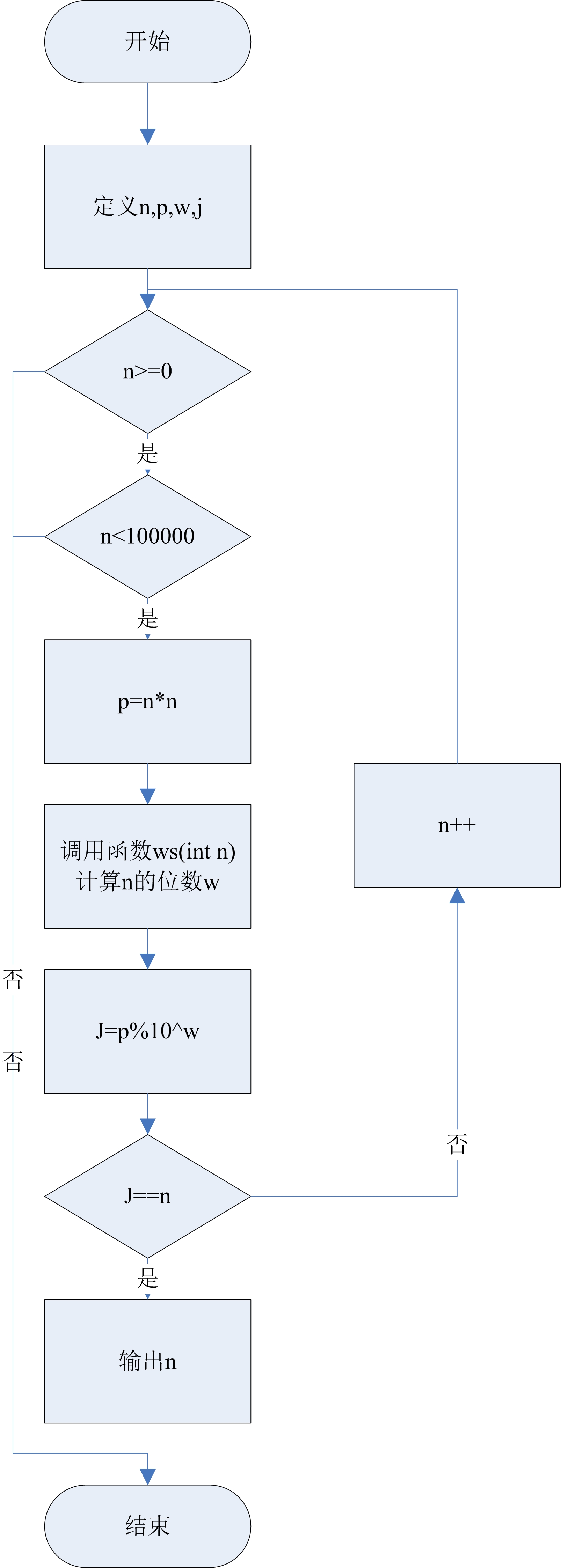
①、我们可以定义long类型数,算出这个数的平方。
②、我们可以判断这个数的位数,然后对平方数除余(数本身位数+1),得到一个余数,判断是否与自身数相等。
③、如果相等就打印出来。
三、流程图
四、代码实现
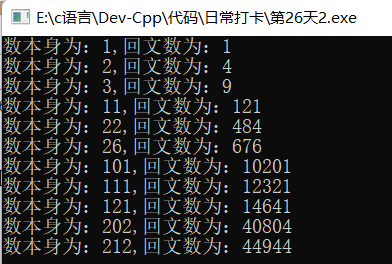
#include<iostream> #include<cmath> using namespace std; long ws(long n) { long count=0; while(n!=0) { count++; n=n/10; } return count; } int main() { long n,p,w,nn; long a; for(n=1;n<100000;n++) { a=1; p=n*n; nn=n; w=ws(n); for(int j=1;j<=w;j++) { a=a*10; } if((p%a)==nn) { cout<<"自守数为:"<<nn<<endl; } } return 0; }
五、结果实现
②、回文数
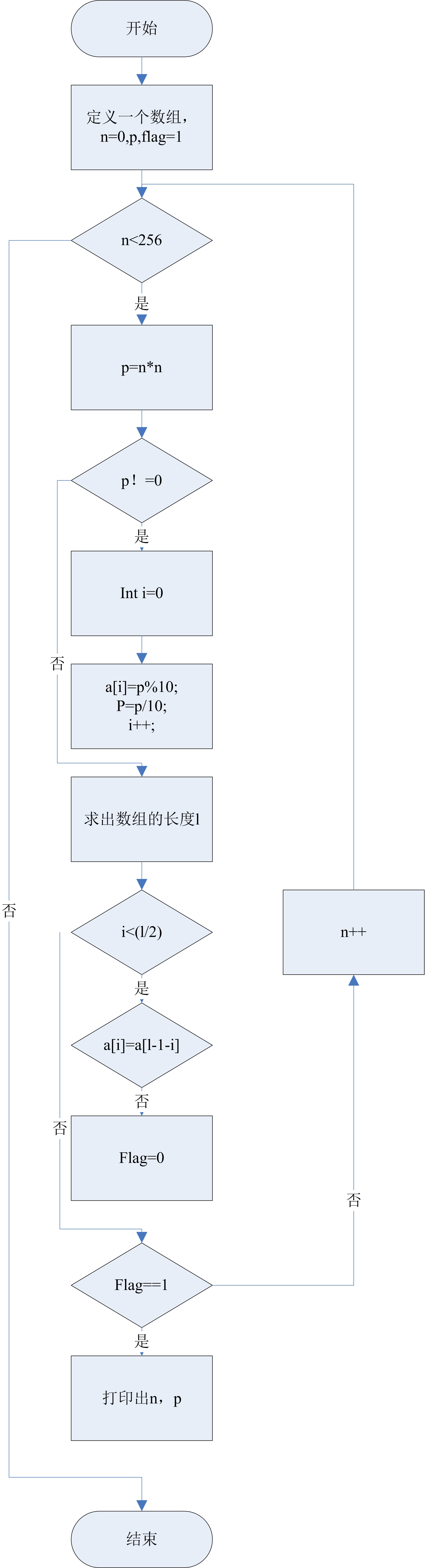
一、问题描述
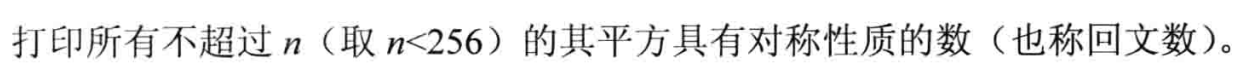
二、设计思路
①、对于n的范围取平方。
②、将平方数拆分到数组中,从头到尾判断数组数字是否一致。
③、如果首尾依次对应相等,就说明这个平方数是回文数,打印出原数和平方数。
三、流程图
四、代码实现
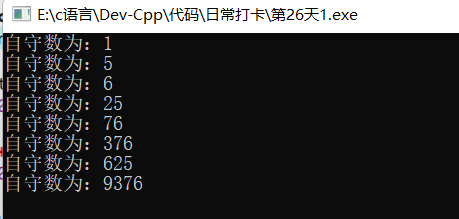
#include<iostream> using namespace std; int main() { int n; long p; int t; long pp; int i; int a[16]; for(n=1; n<256; n++) { p=n*n; pp=0; t=1; for(i=0;p!=0;i++) { a[i]=p%10; p=p/10; } for(; i>0; i--) { pp+=a[i-1]*t; t=t*10; } if(pp==(n*n)) { cout<<"数本身为:"<<n<<",回文数为:"<<pp<<endl; } } return 0; }
五、代码实现