c++打卡第十一天
一、问题描述
牛顿迭代法求方程根。
编写一个函数用来实现牛顿迭代法求方程根。方程为为ax^4+bx*3+cx^2+dx+e=0,系数由系统输入,求x在1附近的一个实根,由主函数输出。
x=x0-f(x0)/fd(x0),当 x减去x0的绝对值小于等于1e-5即十的负五次方时,程序结束。
二、设计思路。
①一个简单的函数,使用循环实现,我们可以注意到,这里存在两个自变量x以及x0,而x的值需要我们自己确定,我们在这里也通过程序输入,实现不同的结果。
②我们要注意,x我们赋值时要在1附近赋值,不要差距过大。
③求导的公式需要我们自己书写。
④我们需要调用绝对值函数,此时需要调用头文件#include<cmath>,其实可以再次编写一个函数来实现绝对值。
三、流程图
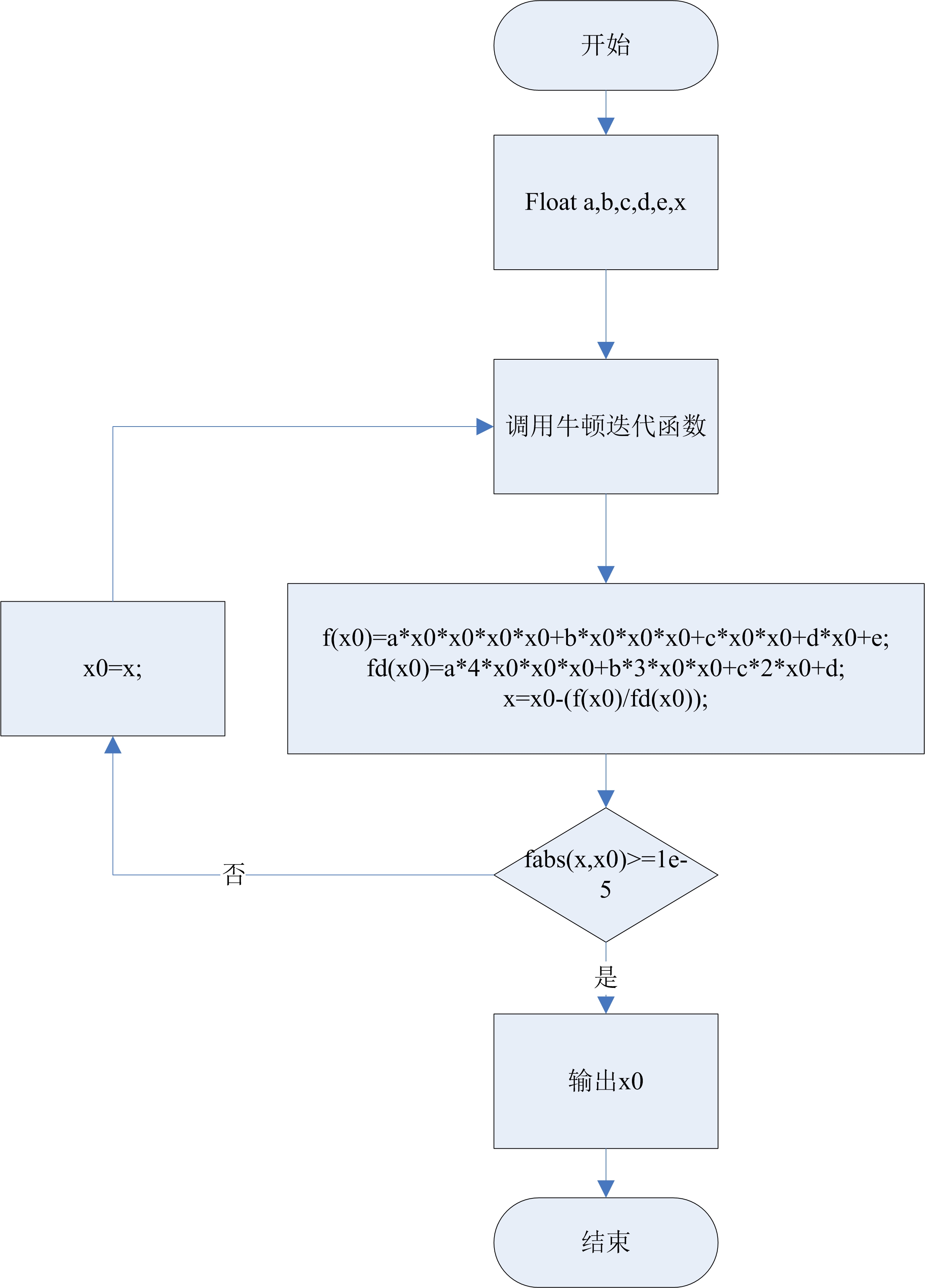
四、代码实现。
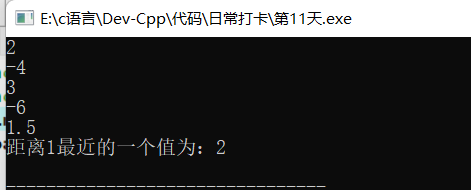
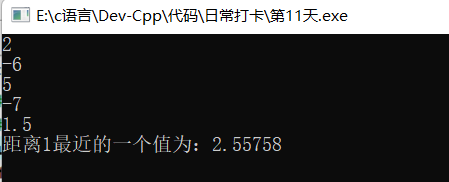
#include<iostream> #include<cmath> using namespace std; float nd(float a,float b,float c,float d,float x) { float f,fd,x0; do { x0=x; f=a*x0*x0*x0+b*x0*x0+c*x0+d; fd=a*3*x0*x0+b*2*x0+c; x=x0-(f/fd); } while(fabs(x-x0)>1e-5); return x; } int main() { float a,b,c,d,x; cin>>a; cin>>b; cin>>c; cin>>d; cin>>x; float t=nd(a,b,c,d,x); cout<<"距离1最近的一个值为:"<<t<<endl; return 0; }
五、代码实现