c++打卡第六天

Ⅰ

一、问题描述

定义一个函数判断一个数是否为质数。

二、设计思路

①输入一个数，同时进入函数判断。

②进入函数可以通过for循环判断n是否为质数

③当这个数为1 时，不是质数，而当这个数是2 3时，是质数。

④可以通过循环质因数，其范围到n的开平方。

三、流程图

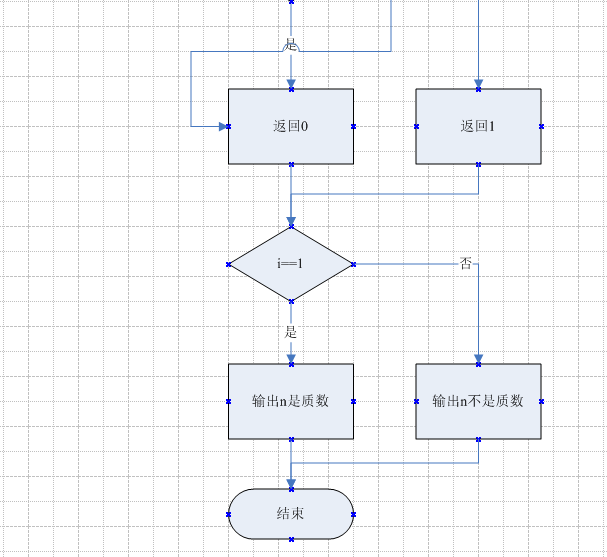
四、代码实现

 

#include<iostream>
#include<cmath>
using namespace std;
int is_prime(int x)
{
   if(x==1)
   {
       return 0;
   }
    else
    {
    for(int i=2;i<=sqrt(x);i++)
    {
        if(x%i==0)
        {
            return 0;
        }    
    }
    }
    return 1;
}
int main()
{
    int n;
    cin>>n;
    int len=is_prime(n);
    if(len==1)
    {
        cout<<n<<"是质数"<<endl; 
    }
    else
    {
        cout<<n<<"不是质数"<<endl;
    }
    return 0;
}

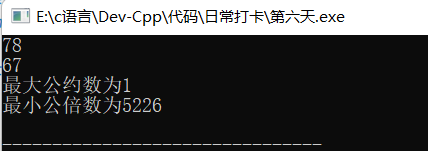
五、运行结果

 Ⅱ

一、问题描述

编写函数求两个数的最大公约数和最小公倍数

二、设计思路

①、输入两个数a，b，同时对这两个数排序，将大数拍到前面。

②、调用求最大公约数的函数，如果小数为0的话那么最大公约数为大数。

③、否则使用辗转相除法，大数除余小数，此时将小数赋值为大数a，余数赋值为b，继续调用函数。最终直到小数b为0，返回a。

④、a与b的乘积等于最大公约数乘以最小公倍数。

三、流程图

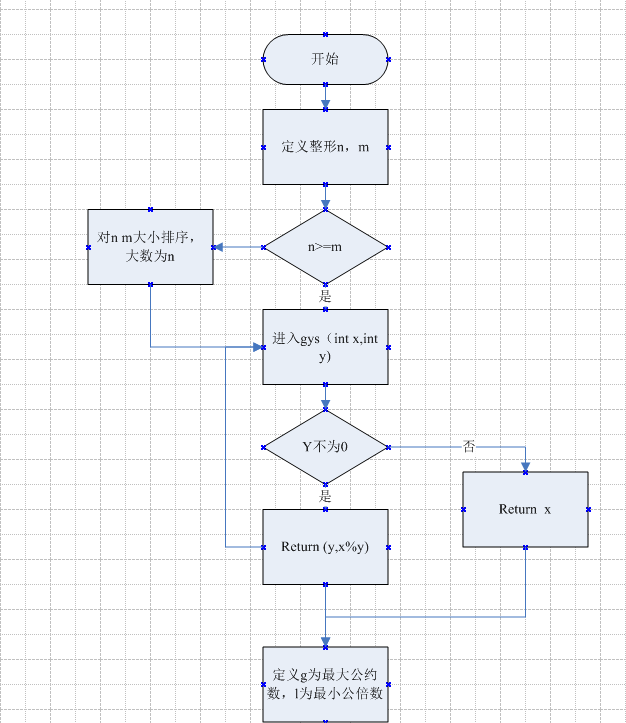
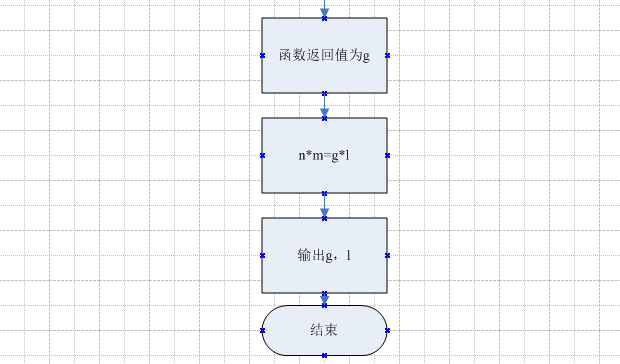
 四、代码实现

#include<iostream>
using namespace std;
int gys(int x,int y)
{
    if(y==0)
    {
        return x;
    }
    return gys(y,x%y);
}
int main()
{
    int a,b;
    cin>>a;
    cin>>b;
    int t;
    if(a<b)
    {
        t=a;
        a=b;
        b=t;
    }
    int g=gys(a,b);
    int l=(a*b)/g;
    cout<<"最大公约数为"<<g<<endl;
    cout<<"最小公倍数为"<<l<<endl; 
    return 0;
}

五、代码实现