poj-2142-exgcd/解的和最小
Description Ms. Iyo Kiffa-Australis has a balance and only two kinds of weights to measure a dose of medicine. For example, to measure 200mg of aspirin using 300mg weights and 700mg weights, she can put one 700mg weight on the side of the medicine and three 300mg weights on the opposite side (Figure 1). Although she could put four 300mg weights on the medicine side and two 700mg weights on the other (Figure 2), she would not choose this solution because it is less convenient to use more weights.
You are asked to help her by calculating how many weights are required. 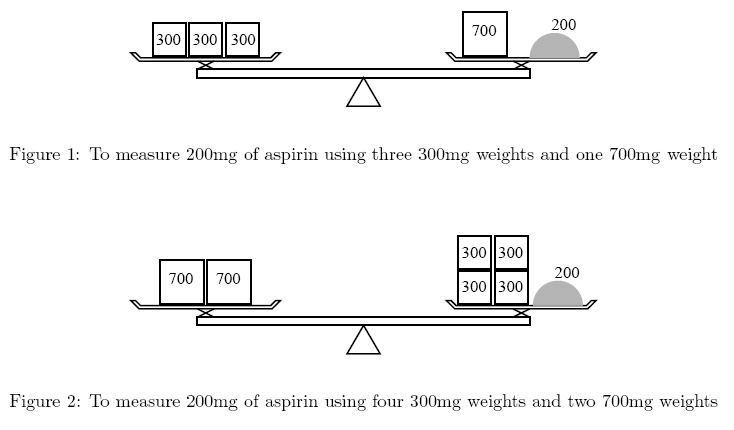 Input The input is a sequence of datasets. A dataset is a line containing three positive integers a, b, and d separated by a space. The following relations hold: a != b, a <= 10000, b <= 10000, and d <= 50000. You may assume that it is possible to measure d mg using a combination of a mg and b mg weights. In other words, you need not consider "no solution" cases.
The end of the input is indicated by a line containing three zeros separated by a space. It is not a dataset. Output The output should be composed of lines, each corresponding to an input dataset (a, b, d). An output line should contain two nonnegative integers x and y separated by a space. They should satisfy the following three conditions.
No extra characters (e.g. extra spaces) should appear in the output. Sample Input 700 300 200
500 200 300
500 200 500
275 110 330
275 110 385
648 375 4002
3 1 10000
0 0 0
Sample Output 1 3
1 1
1 0
0 3
1 1
49 74
3333 1
Source |
给出两种砝码质量为a,b,问能不能测出质量c的东西,求最小的砝码数量,如果有多个方案考虑总质量最小的方案。
a*x+b*y=c ,求满足方程的 abs(x)+abs(y)的最小值。做两次exgcd取一个最优的。一次让x为最小正整数,一次让y为最小正整数。
(但我总觉得应该让求出来的解在减去一个d'/d看会不会更优,这里没进行这一步但是A了。
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 using namespace std; 5 #define LL long long 6 #define mp make_pair 7 #define pb push_back 8 #define inf 0x3f3f3f3f 9 void exgcd(LL a,LL b,LL &d,LL &x,LL &y){ 10 if(!b){d=a;x=1;y=0;} 11 else{exgcd(b,a%b,d,y,x);y-=(a/b)*x;} 12 } 13 int main(){ 14 LL a,b,c,d,x1,x2,y1,y2; 15 while(cin>>a>>b>>c&&(a||b||c)){ 16 exgcd(a,b,d,x1,y1); 17 exgcd(b,a,d,x2,y2); 18 if(c%d){ 19 puts("no solution"); 20 } 21 else{ 22 LL d1=b/d,d2=a/d; 23 x1=x1*c/d,y1=y1*c/d; 24 x2=x2*c/d,y2=y2*c/d; 25 x1=(x1%d1+d1)%d1,y1=(c-a*x1)/b; 26 x2=(x2%d2+d2)%d2,y2=(c-b*x2)/a; 27 x1=fabs(x1),y1=fabs(y1); 28 x2=fabs(x2),y2=fabs(y2); 29 if(x1+y1<x2+y2) cout<<x1<<' '<<y1<<endl; 30 else if(x1+y1>x2+y2) cout<<y2<<' '<<x2<<endl; 31 else{ 32 if(x1*a+y1*b<x2*a+y2*b) cout<<x1<<' '<<y1<<endl; 33 else cout<<y2<<' '<<x2<<endl; 34 } 35 } 36 } 37 return 0; 38 }




