求解最近公共点对
给出位于平面坐标系上的n个点,找到一对点使得这对点的距离尽可能的小,求这个最小的距离是多少。
如果这些点是在一维情况下很容易想到分治,ans=min(solve(l,mid),solve(mid+1,r),temp),temp显然是dis(p[i],p[j])(i点为处于S1集合且最靠近中线的点,j是处于S2集合最靠近中线的点),跨越两个点集又使得距离最小只能是中间的两个点了,还有一个显然的推论是:如果ans=temp,就说明i,j两点到中线的距离一定都小于d'=min(solve(l,mid),solve(mid+1,r));
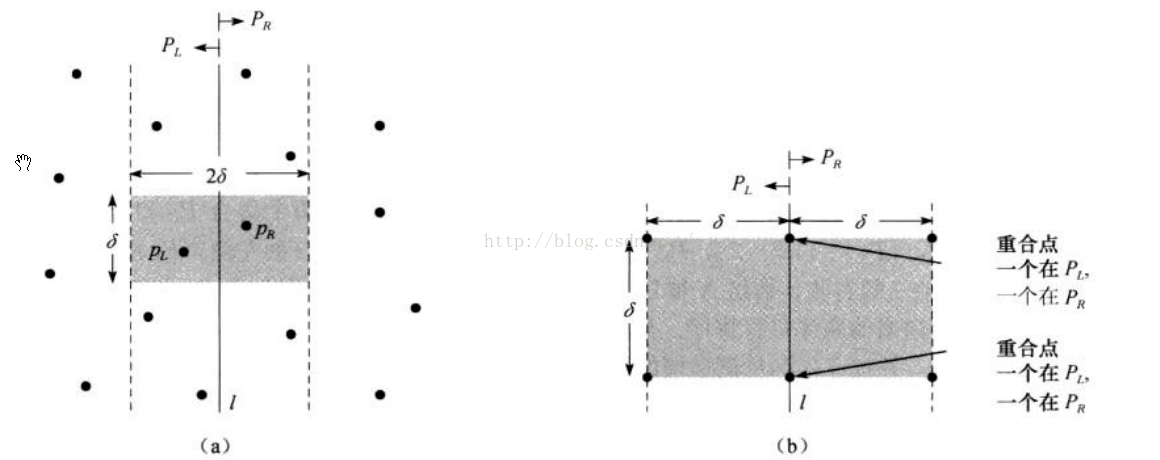
对于二维的情况,同样我们筛去的点是横坐标距离中线大于d'的点,可以看出选这些点一定不会优于d'。也就是说我们检查的点如下图所示:
 //S下方的点是待检查点
//S下方的点是待检查点
对于这些待检查点如果直接暴力的话还是不可行,万一待检查点数目过多得话复杂度还是接近于N^2,还是不行,我们可以缩小遍历范围。(前提是分治求出了d')
对于SL区域下内所有点,任意两点间距必定不小于d',SR也同理,所以如果我们在SL(SR)区域内画出一个d'*2d'的矩形的话,这个矩形内最多只有六个点,也就是下面这图(b)这种情况:
具体证明不怎么会= =
那么同理我们可以推出在S内画出一个2d'*2d'的矩形的话,矩形内不会超过12个点,也就是说我们对于S内的点按照y坐标升序排列之后,只需遍历每个点上面的十二个点就好了,超过这个数的点一定在矩形之外,纵坐标之差大于d',一定不会是最优解了。这样的话复杂度就降低很多。
例题: https://www.nowcoder.com/acm/contest/59/E
要求的就是<i,pre[i]>最大的距离平方。
代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 #define LL long long 4 const LL INF=1LL<<62; 5 struct Point 6 { 7 LL x,y; 8 Point(){} 9 Point(LL _x,LL _y):x(_x),y(_y){} 10 }p[101000],q[101000]; 11 int pre[101000]; 12 bool cmpx(Point A,Point B){return A.x<B.x;} 13 bool cmpy(Point A,Point B){return A.y<B.y;} 14 LL dis(Point A,Point B){return (A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y);} 15 LL solve(int left,int right) 16 { 17 if(left>=right) return INF; 18 if(left+1==right) return dis(p[left],p[right]); 19 int mid=(left+right)>>1; 20 LL res=min(solve(left,mid),solve(mid+1,right)); 21 int s=0; 22 for(int i=left;i<=right;++i){ 23 if(p[i].x>=p[mid].x-res&&p[i].x<=p[mid].x+res) q[s++]=p[i]; 24 } 25 sort(q,q+s,cmpy); 26 for(int i=0;i<s;++i){ 27 for(int j=i+1;j<s&&j-i<10;++j){ 28 if(q[j].y-q[i].y>=res) break; 29 res=min(res,dis(q[i],q[j])); 30 } 31 } 32 return res; 33 } 34 int main() 35 { 36 int n,i,j,k,x; 37 while(cin>>n){ 38 for(i=1;i<=n;++i){ 39 scanf("%d",&x); 40 pre[i]=pre[i-1]+x; 41 p[i]=Point(i,pre[i]); 42 } 43 sort(p+1,p+1+n,cmpx); 44 printf("%lld\n",solve(1,n)); 45 } 46 return 0; 47 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号