CCF-CSP201803-4-棋局评估
问题描述
Alice和Bob正在玩井字棋游戏。
井字棋游戏的规则很简单:两人轮流往3*3的棋盘中放棋子,Alice放的是“X”,Bob放的是“O”,Alice执先。当同一种棋子占据一行、一列或一条对角线的三个格子时,游戏结束,该种棋子的持有者获胜。当棋盘被填满的时候,游戏结束,双方平手。
Alice设计了一种对棋局评分的方法:
- 对于Alice已经获胜的局面,评估得分为(棋盘上的空格子数+1);
- 对于Bob已经获胜的局面,评估得分为 -(棋盘上的空格子数+1);
- 对于平局的局面,评估得分为0;
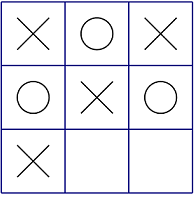
例如上图中的局面,Alice已经获胜,同时棋盘上有2个空格,所以局面得分为2+1=3。
由于Alice并不喜欢计算,所以他请教擅长编程的你,如果两人都以最优策略行棋,那么当前局面的最终得分会是多少?
井字棋游戏的规则很简单:两人轮流往3*3的棋盘中放棋子,Alice放的是“X”,Bob放的是“O”,Alice执先。当同一种棋子占据一行、一列或一条对角线的三个格子时,游戏结束,该种棋子的持有者获胜。当棋盘被填满的时候,游戏结束,双方平手。
Alice设计了一种对棋局评分的方法:
- 对于Alice已经获胜的局面,评估得分为(棋盘上的空格子数+1);
- 对于Bob已经获胜的局面,评估得分为 -(棋盘上的空格子数+1);
- 对于平局的局面,评估得分为0;
例如上图中的局面,Alice已经获胜,同时棋盘上有2个空格,所以局面得分为2+1=3。
由于Alice并不喜欢计算,所以他请教擅长编程的你,如果两人都以最优策略行棋,那么当前局面的最终得分会是多少?
输入格式
输入的第一行包含一个正整数T,表示数据的组数。
每组数据输入有3行,每行有3个整数,用空格分隔,分别表示棋盘每个格子的状态。0表示格子为空,1表示格子中为“X”,2表示格子中为“O”。保证不会出现其他状态。
保证输入的局面合法。(即保证输入的局面可以通过行棋到达,且保证没有双方同时获胜的情况)
保证输入的局面轮到Alice行棋。
每组数据输入有3行,每行有3个整数,用空格分隔,分别表示棋盘每个格子的状态。0表示格子为空,1表示格子中为“X”,2表示格子中为“O”。保证不会出现其他状态。
保证输入的局面合法。(即保证输入的局面可以通过行棋到达,且保证没有双方同时获胜的情况)
保证输入的局面轮到Alice行棋。
输出格式
对于每组数据,输出一行一个整数,表示当前局面的得分。
样例输入
3
1 2 1
2 1 2
0 0 0
2 1 1
0 2 1
0 0 2
0 0 0
0 0 0
0 0 0
1 2 1
2 1 2
0 0 0
2 1 1
0 2 1
0 0 2
0 0 0
0 0 0
0 0 0
样例输出
3
-4
0
-4
0
样例说明
第一组数据:
Alice将棋子放在左下角(或右下角)后,可以到达问题描述中的局面,得分为3。
3为Alice行棋后能到达的局面中得分的最大值。
第二组数据:
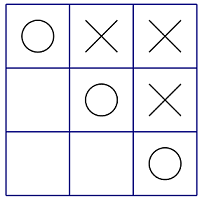
Bob已经获胜(如图),此局面得分为-(3+1)=-4。
第三组数据:
井字棋中若双方都采用最优策略,游戏平局,最终得分为0。
Alice将棋子放在左下角(或右下角)后,可以到达问题描述中的局面,得分为3。
3为Alice行棋后能到达的局面中得分的最大值。
第二组数据:
Bob已经获胜(如图),此局面得分为-(3+1)=-4。
第三组数据:
井字棋中若双方都采用最优策略,游戏平局,最终得分为0。
数据规模和约定
对于所有评测用例,1 ≤ T ≤ 5。
博弈,f[S]表示S状态下的得分情况,正数表示胜利负数表示输,0表示平局。
边界情况是:1)当前棋局已经有玩家胜出,此时f[S]= -(空格数+1).由于状态都合法,所以此时一定是对手胜利而轮到自己下棋,所以此时的f[S]是负数表示自己输了,且对手可以获得-f[S]分数。
2)当前棋局已经没有空位,且未决出胜负。此时f[S]=0;
转移的时候,每个人都先考虑是否能赢,能赢的话挑分数大的状态转移。
不能赢考虑是否能平,不能平只能输,选一个输的最小的状态。
1 #include<bits/stdc++.h> 2 using namespace std; 3 #define pii pair<int,int> 4 map<string,int>f; 5 int blank(string str){ int res=0; for(char c:str)res+=(c=='0');return res; } 6 int check(string str){ 7 for(int i=0;i<3;++i){ 8 if(str[i*3]=='1'&&str[i*3+1]=='1'&&str[i*3+2]=='1') return 1; 9 if(str[i*3]=='2'&&str[i*3+1]=='2'&&str[i*3+2]=='2') return 2; 10 if(str[i]=='1'&&str[i+3]=='1'&&str[i+6]=='1') return 1; 11 if(str[i]=='2'&&str[i+3]=='2'&&str[i+6]=='2') return 2; 12 } 13 if(str[0]=='1'&&str[4]=='1'&&str[8]=='1'|| 14 str[2]=='1'&&str[4]=='1'&&str[6]=='1')return 1; 15 if(str[0]=='2'&&str[4]=='2'&&str[8]=='2'|| 16 str[2]=='2'&&str[4]=='2'&&str[6]=='2')return 2; 17 return 0; 18 } 19 void dfs(string state,int cur){ 20 if(f.count(state))return; 21 //cout<<state<<endl; 22 int r=check(state); 23 int b=blank(state); 24 if(r==1){ 25 f[state]=-b-1; 26 }else if(r==2){ 27 f[state]=-b-1; 28 }else if(b==0){ 29 f[state]=0; 30 } 31 else{ 32 int win=-999,lose=-999,ping=-999; 33 for(int i=0;i<=8;++i){ 34 if(state[i]=='0'){ 35 if(cur==1){ 36 state[i]='1'; 37 dfs(state,2); 38 }else if(cur==2){ 39 state[i]='2'; 40 dfs(state,1); 41 } 42 if(f[state]<0){ 43 win=max(win,-f[state]); 44 }else if(f[state]>0){ 45 lose=max(lose,-f[state]); 46 }else ping=1; 47 state[i]='0'; 48 } 49 } 50 if(win!=-999){ 51 f[state]=win; 52 }else if(ping!=-999)f[state]=0; 53 else f[state]=lose; 54 } 55 } 56 int main(){ 57 int T; 58 char ch; 59 string str; 60 cin>>T; 61 while(T--){ 62 str=""; 63 for(int i=1;i<=9;++i){ 64 cin>>ch; 65 str+=ch; 66 } 67 if(!f.count(str)){ 68 dfs(str,1); 69 }cout<<f[str]<<endl; 70 } 71 return 0; 72 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号