CVPR2020_Improved Few-Shot Visual Classification

文章链接：URL: https://arxiv.org/pdf/1912.03432.pdf

核心概述

本文作者从距离度量角度出发，探讨了现行SoTA FSL方法的优缺点，并且提出了一种simple CNAPS方法，特征提取部分采用的是ResNet18+FiLM层（自适应任务）；最终分分类采用了马氏（ Mahalanobis）距离。 作者重点论证了马氏距离与现下最常用的欧氏距离（L2）、曼哈顿距离（L1）以及负点积（余弦相似度）等距离度量相比，其在类间差异性求解上的优越点。同时作者认为：影响FSC准确性的关键因素是距离度量的选择，而非特征提取器的鲁棒性。

总结：

• contribution:

  • 分类用了 基于类协方差的距离度量（即马氏距离） ，将CNAPS的性能提升了6.1％。
  • 在shot数量极小（4）的情况下，也可以构建class-specific的协方差，使距离求解可行。
  • 提出了一种新的“simple-CNAPS”体系结构，极大减少了参数量 （占总数的3.2％-9.2％），分类过程不可学习，参数固定，效果依然很好。

• why work:

  • resnet+FiLM自适应特征提取
  • 马氏距离分类（通过求解协方差矩阵，去除各个分量之间的方差，消除了量纲性，并且加入的对数据分布的先验信息更少）。
    

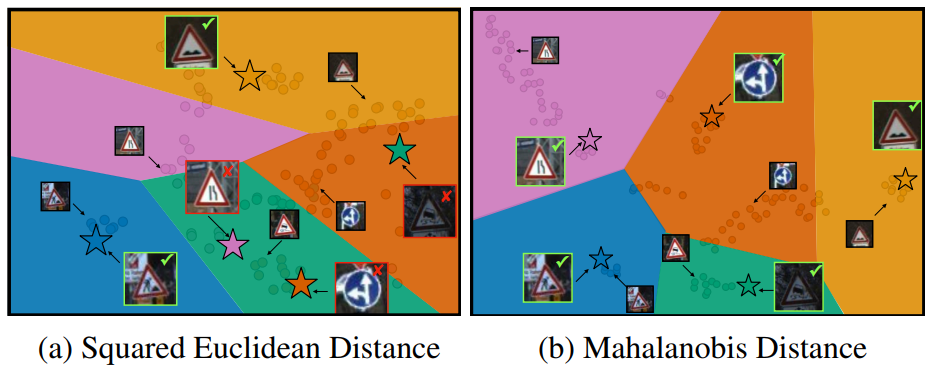
图1：类协方差度量：点代表embedded图像feature, 各个颜色交接处即为类决策边界，五角星代表query image。左图：标准 L2-based距离，即欧式距离， 右图：马氏距离（基于类别协方差的距离度量）。为了方便比较，我们把有图做了空间转换，即搞成了线性分割面。数据集：features: out-of-domain Traffic Signs dataset。该任务共包含五个类共112个support samples, 每个类一个query instance。我们（右）的决策边界与support embedding对齐的更好，并且全都分类正确，基于L2的分类器有三类都分错了。

---

算法部分

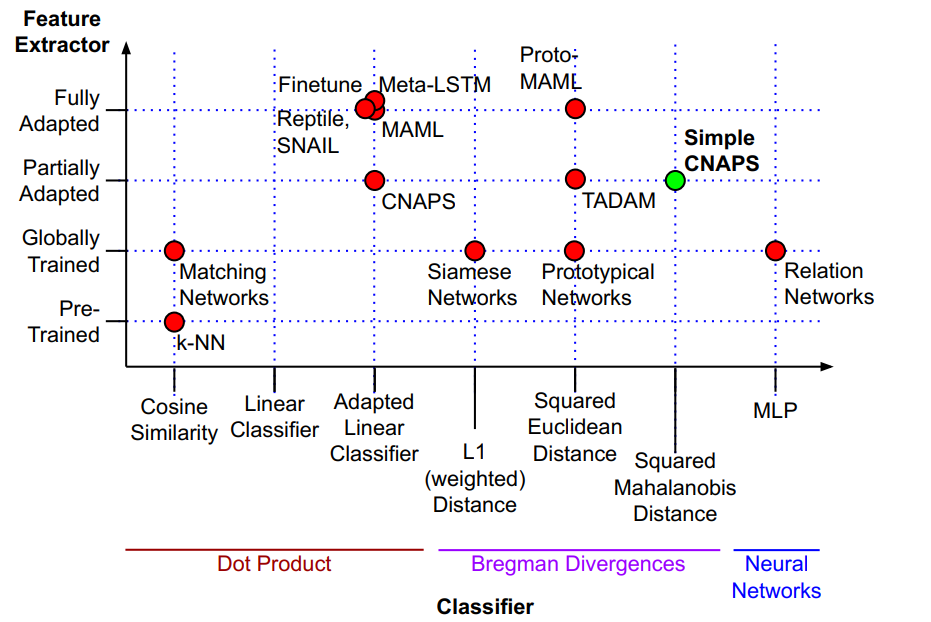
下图是对现行FSL方法的可视化。横轴：特征提取器的自适应性策略；纵轴：分类方法。

模型结构图如下图所示。作者是在CNAPS模型基础上开发的，特征提取部分的结构相同，都是部分自适应的结构（ResNet18+FiLM层：自适应模块，对每个block的feature做适配当前任务的shift+scale，用support set训得），主要差异在于分类上，原始的CNAPS采用的是一个可学习的线性分类器，最后经过softmax处理得到分类结果，本文的simple-CNAPS直接采用马氏距离进行距离求解，没有参数，只需要计算协方差矩阵即可，
即分类结果=softmax( \(D_M\) (suport mean embedding, query embedding))。

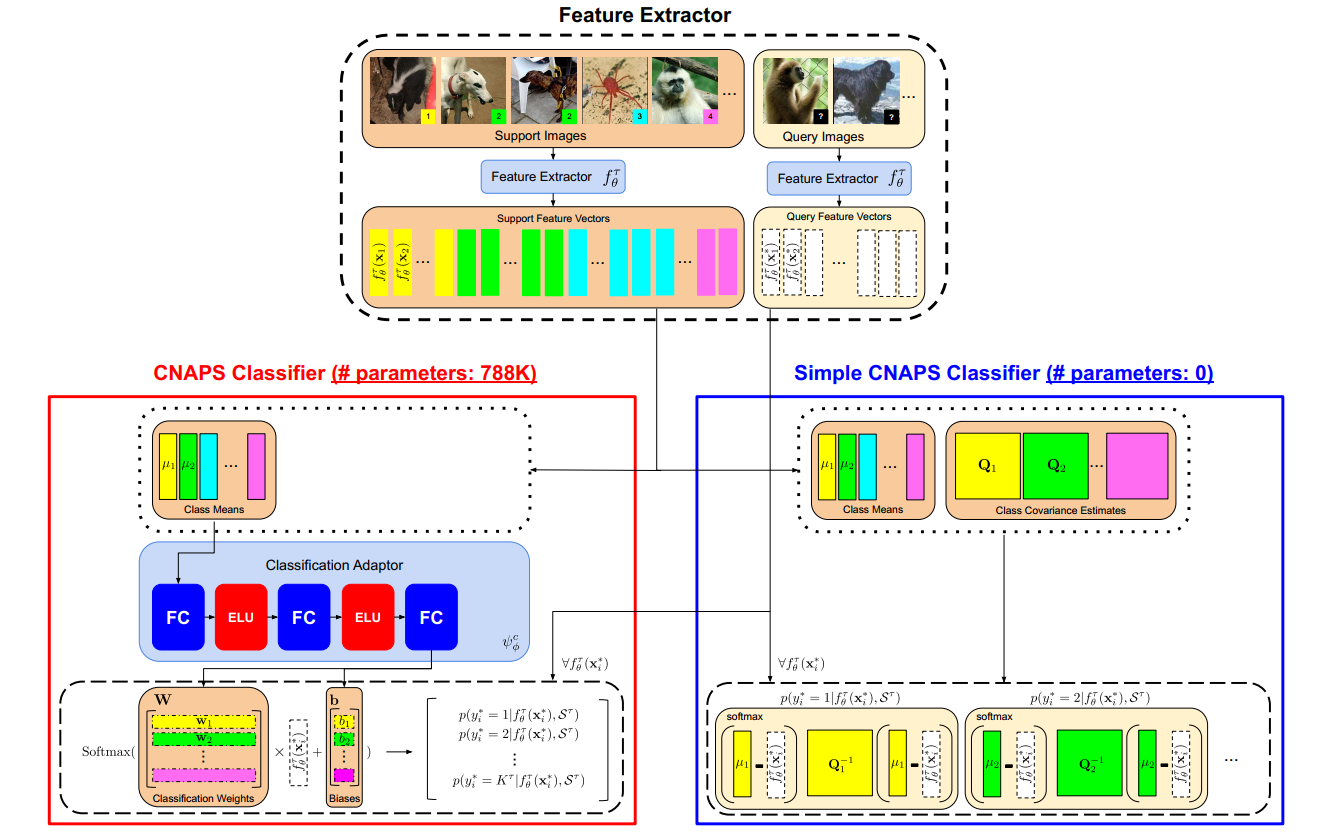
1. feature extractor:

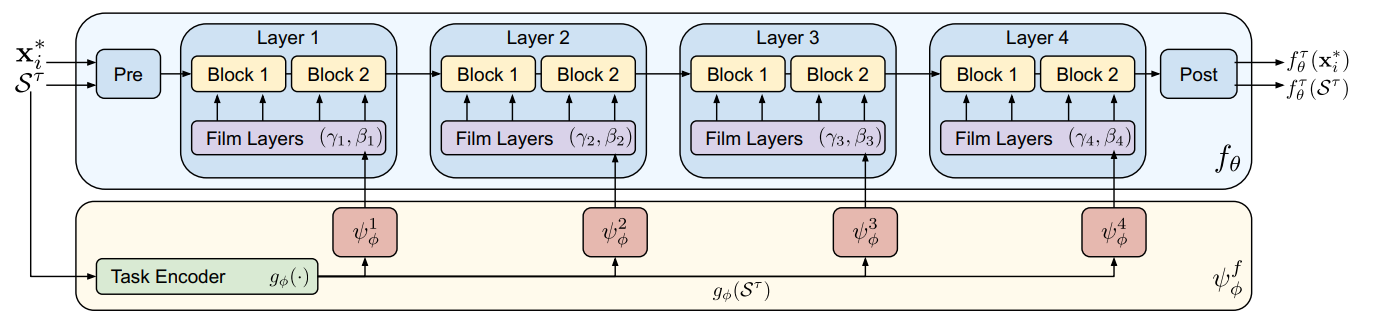
resnet18的feature blocks在imagenet上做了预训练，然后将每个block出的support feature送到一个FiLM层 \(\psi_\phi^i\) 学习自适应参数 \((\gamma_i, \beta_i)\) ，训好的 \(\psi_\phi^i\) 对i层的coarse feature做shift+scale处理，使feature适配当前任务，忽略非相关特征区域（类似于attention）。

2. classification

2.1 老版的CNAPS：

分类通过一个可学习的线性分类adapter完成。分类结果= \(softmax(W f_\theta^\Gamma(x_i^*)+b)\) ，W和b由分类自适应网络 \(\psi_\phi^c\) 产生。

\[[W, b] = [\psi_\phi^c(\mu_1), \psi_\phi^c(\mu_2), ..., \psi_\phi^c(\mu_k)]^T \]

对于类别k，对应行（第k行）的类权重是 \(\psi_\phi^c(\mu_k)\) 的类均值 \(\mu_k\)(平均池化) 。

2.2 simple-CNAPS

分类概率计算公式（k表示第k类）：

\[p(y_i^∗|f_\theta^\Gamma(x_i^*); S^\Gamma) = softmax(−d_k(f_\theta^\Gamma(x_i^*); \mu_k)) \]

其中 \(d_k\) 即为马氏距离：

\[d_k(x, y) = \frac{1}{2}(x − y)^T (Q^\Gamma_k)^{−1}(x − y) \]

\(Q^\Gamma_k\) 是task and class-specific的协方差矩阵。考虑到support set中shot数量可能远小于特征空间维度，对协方差矩阵做正则化（保证可逆）：

\[Q^\Gamma_k = \lambda_k^\Gamma \Sigma_k^\Gamma + (1-\lambda_k^\Gamma)\Sigma^\Gamma + \beta I \]

其中 \(\Sigma_k^\Gamma\) 是类内（ class-within-task）协方差矩阵， \(\Sigma^\Gamma\) 是类间（all-classes-in-task）协方差矩阵(忽略类别信息。 疑问： \(\mu\) 如何解？所有embedding做平均池化？)。 \(\Sigma_k^\Gamma\) 表达式（ \(S^\Gamma\) ：support set ）：

\[\Sigma_k^\Gamma = \frac{1}{S^\Gamma-1}(\sum_{(x_i, y_i)\in S^\Gamma}(f_\theta^\Gamma(x_i)-\mu_k)(f_\theta^\Gamma(x_i)-\mu_k)^T) \]

作者将比例 \(\lambda\) 定义为： \(\lambda_\Gamma^k =|S_\Gamma^k|/(|S_\Gamma^k|+1)\) 。

• 当 \(|S_\Gamma|=1，Q_\Gamma^k= 0.5\Sigma^\Gamma +\beta I\) , 此时 \(Q_\Gamma^k\) 依赖于正则化参数β的大小（接近欧氏距离）。
• 当 \(|S_\Gamma^k|=2，\lambda_\Gamma^k =2/3，Q_\Gamma^k=2/3\Sigma_k^\Gamma+1/3\Sigma^\Gamma+\beta I\) ，即 \(Q_\Gamma^k\) 此时受类内协方差的影响更大，受all-classes-in-task协方差矩阵 \(\Sigma^\Gamma\) 的影响更小。
• 在high-shot情况下， \(\lambda_\Gamma^k\) 的值趋近于1，即完全受类内协方差矩阵影响（class-level covariance）。

直观理解: shot数量越多， \(\lambda_\Gamma^k\) 越大，class-within-task协方差 \(\Sigma_k^\Gamma\) 的估计越准确，\(Q_\Gamma^k\) 的值应由 \(\Sigma_k^\Gamma\) 决定。 作者还考虑了把 \(\lambda_\Gamma^k\) 设置为可学习参数的方法，结果表明就这种直接设定的方式效果最好。

经过softmax（马氏距离），等价于多元高斯分布：

\[p(y_i^*=k|f_\theta^\Gamma(x_i^*), S^\Gamma) = \frac{\pi_k \mathcal{N}(\mu_k, Q_k^\Gamma)}{\sum_{k'} \pi_{k'}\mathcal{N}(\mu_{k'}, Q_{k'}^\Gamma)} \]

高斯混合系数 \(\pi_k=1/k\) （系数相等，每个分量的contribution相同。类比欧氏距离，其约定高斯分量在 \(\mu_k\) 附近服从方差为1 \(Q_k^\Gamma=1\) 的单位正态分布，即提前设定了每个类别的方差是一致的）。

Experiment Detail

数据集： meta-datasets: ILSVRC-2012（ImageNet），Omnilot ，FGVC-Aircraft，CUB-200-2011（Birds），Describable Textures（DTD)，QuickDraw ，FGVCx Fungi（Fungi），VGG Flower（Flower），Traffic Signs (Signs)和MSCOCO。前八个训练，后两个测试（域外）， 前八个中选了少量做域内测试。

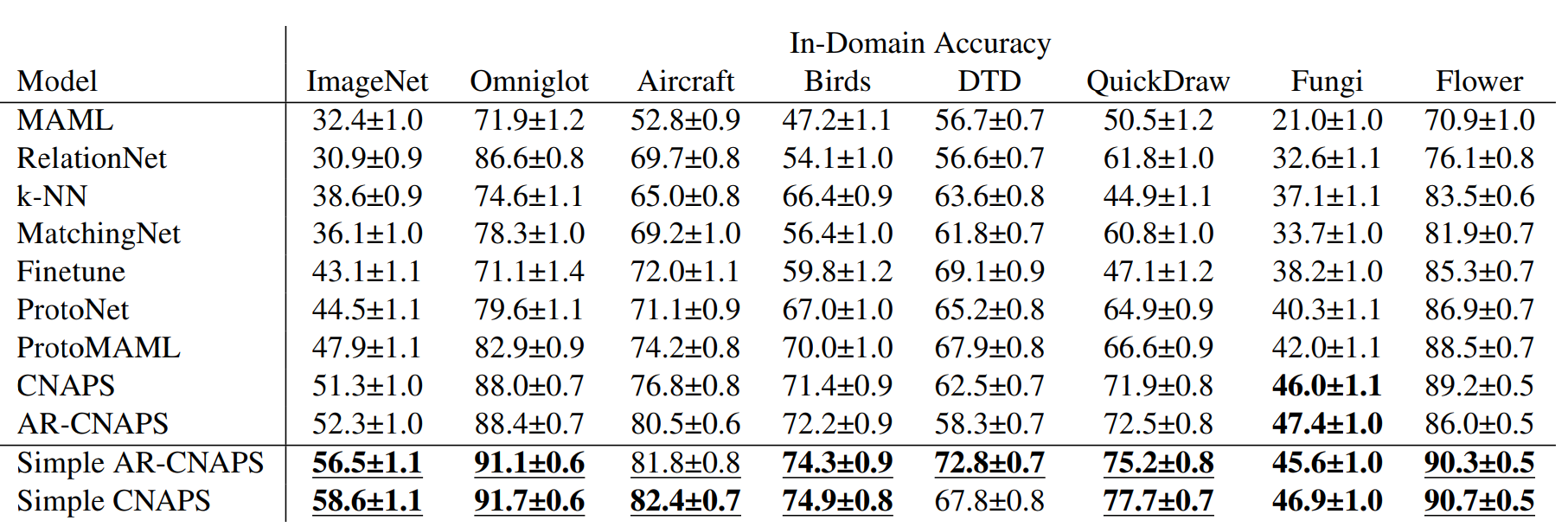
与其他距离度量的对比（L1, squared L2，负点积）

Thoughts

算法结构比较简单，大多在理论论述，创新点主要在于马氏距离应用到特征空间的距离度量上。作者认为特征提取器的构建对最终分类准确性的影响没有“分类指标”的影响大，个人认为feature embedding这一步还是很重要的，可以考虑更end-to-end的结构，比如attention这种，另外作者也没说是在哪一个block出来的feature上求距离，考虑多尺度都做会不会提点？