MOSSE_Visual Object Tracking using Adaptive Correlation Filters学习笔记

> 论文部分

基于相关滤波的tracker鼻祖论文 MOSSE
《Visual Object Tracking using Adaptive Correlation Filters》 CVPR 2010

0. Abstract

虽然相关略波器并不常用，但是其可以通过旋转，遮挡以及其他干扰的方式来有效跟踪复杂目标，并且能达到优于当前最新技术的速度。最早最简单的相关滤波器才哟个简单模板，在跟踪过程中基本上都是以失败告终。近来，诸如ASEF以及UMACE的最新技术则表现得更好，但是他们的训练需求远远无法达到跟踪的要求。视觉跟踪任务需要跟踪器在第一帧上进行充分地学习，以动态适应目标对象的形变。

本文提供了一种新的相关滤波器——平方误差最小输出和滤波器（MOSSE），其可以在初始帧上产生稳定的相关滤波器。基于MOSSE的跟踪器能够很鲁棒地应对光照，尺度，只是以及非刚性形变等变化对跟踪的影响，同时能够达到每秒669帧的速度。是否产生遮挡是根据peak-tosidelobe比率检测的，所以跟踪器能够在对象消失时暂停检测，并在对象再次出现重新开始检测。

1. Introduction

视觉跟踪在视频处理领域有很多实际性的应用需求。当对象出现在视频的某一帧时，在后续帧中保持对该对象的跟踪是很有用的。每一帧上成功跟踪到的对象能够提供关于该目标更多的实体性和活动性的信息。而跟踪与检测相比又容易得多，因为检测算法需要在每一帧上执行对象检测，跟踪算法相比来说计算量更小。

视觉跟踪近年来收到了更多关注。有许多相当鲁棒的跟踪器被提出，他们可以容忍目标外观的变化并在对象具有复杂运动时保持跟踪效果。最近的例子包括：Incremental Visual Tracking (IVT) [17], Robust Fragments-based Tracking (FragTrack) [1], Graph Based Discriminative Learning (GBDL) [19], and Multiple Instance Learning (MILTrack)[2]。虽然这些算法的性能不错，但是他们太过于复杂，往往包含复杂的外表求解模型或者优化算法，导致检测效率最多只能维持在每秒25到30帧的水平。

在本文中，我们研究了一个更加简单的跟做策略。目标外观的建模通过自适应相关滤波器完成，跟踪过程则利用卷积运算执行。 创建滤波器的比较幼稚的方法（例如从图像中裁剪模板）会为目标产生强烈的峰值，但也会错误地响应背景。这导致它们对目标外观的变化不是特别可靠，并且在挑战性跟踪问题上失败。Average of Synthetic Exact Filters (ASEF), Unconstrained Minimum Average Correlation Energy (UMACE), and Minimum Output Sum of Squared Error (MOSSE) 【本文提出的算法】能够生成对外观变化足够鲁棒的滤波器，对于背景和目标区域的辨别能力强。如图2所示，此类算法能够得到更强的峰值，漂移更少。其中，ASEF和UMACE滤波器离线训练，并运动与对象检测或者对象识别。在本文中，我们利用在线训练的方法更新了此类技术，以自适应方式为跟踪任务服务。实验表明我们的算法能够以最先进的性能进行跟踪，同时保留了基于相关性的方法的大部分速度和简便性。

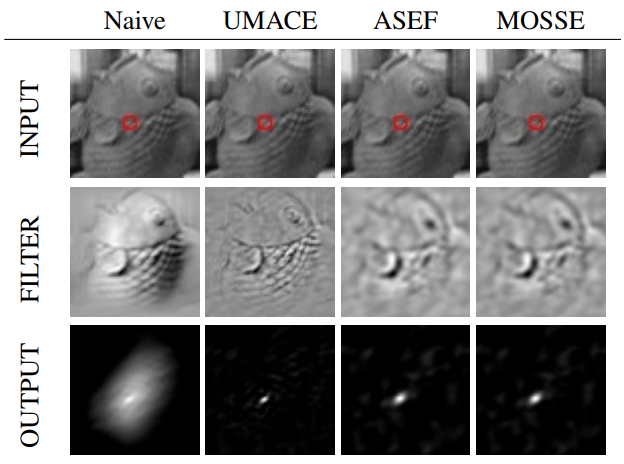
图2：该图显示了Fish视频测试序列第25帧的输入，滤波器和相关输出。 三个新型相关滤波器产生的峰值要比朴素滤波器产生的峰紧凑得多。

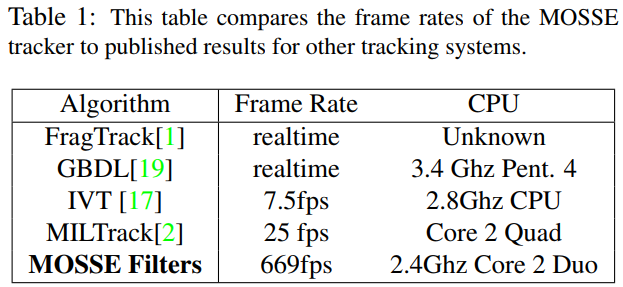
尽管简单，但基于更新后的ASEF，UMACE或MOSSE过滤器的跟踪器在旋转，缩放，照明和部分遮挡的变化下仍然表现良好（参见图1）。 测量相关峰强度的The Peak-to-Sidelobe Ratio (PSR)（PSR）可用于检测遮挡或跟踪失败，停止在线更新以及在对象以类似外观重新出现时重新获取轨道。更一般而言，这些高级相关过滤器可实现与前面提到的更复杂的跟踪器一致的性能。但是，基于过滤器的方法要快20倍以上，并且每秒可以处理669帧（请参见表1）。（优点：简单易执行，性能好，速度快）

图1：该图展示了基于MOSSE滤波器的跟踪器在一些极具挑战性的场景下的检测效果。可见，该检测器可以快速适配尺度以及旋转变化，并且能够处理对象消失以及重新出现的情况。

本文的其余部分安排如下。 第2节回顾了与本文相关的相关滤波技术。 第3节介绍了MOSSE滤波器以及如何使用它创建基于MOSSE的跟踪器。 第4节介绍了来自[17]的七个视频序列的实验结果。 最后，第5节将回顾本文的主要发现。

2. 背景

在1980年代和1990年代，相关滤波器的许多变体被提出，包括合成判别函数（SDF）[7，6]，最小方差合成判别函数（MVSDF）[9]，最小平均相关能量（MACE）[11]，最佳权衡滤波器（OTF）[16]和最小平方误差综合判别函数（MSESDF）[10]。这些过滤器是在具有变化外观和强制性硬约束的目标对象的样本上进行训练的，因此会将始终产生相同高度的峰。最相关的是MACE，它会产生尖峰和高PSR。

在[12]中，作者发现基于SDF的滤波器（如MACE）的硬约束会导致失真容限（distortion tolerance）问题。解决方案是消除硬约束，使得滤波器产生较高的平均相关响应。这种称为“最大平均相关高度（MACH）”的新型“无约束”相关滤波器即为MACE的变体，UMACE。

一种称为ASEF[3]的新型相关过滤器引入了一种针对特定任务调整过滤器的方法。较早的方法仅指定一个峰值，而ASEF指定每个训练图像的整个相关输出。ASEF在眼睛定位[3]和行人检测[4]方面都表现出色。 不幸的是，在两项研究中，ASEF都需要大量训练图像，这对于视觉跟踪来说太慢了。本文通过引入适用于视觉跟踪的ASEF规范化变体来减少数据需求。

3. 基于相关滤波的跟踪算法

基于滤波器的跟踪器使用在初始帧上训练得到的滤波器进行对象外观建模。目标对象通过使用一个以该对象为中心的小窗口进行初始化（第一帧上）。从此刻起，跟踪和滤波器训练同步进行。对目标的跟踪通过在下一帧的搜索窗口上关联过滤器实现； 相关输出中最大值所对应的位置即为跟踪目标的新位置。然后根据该新位置执行滤波器在线更新。

为了创建快速跟踪器（加速），需要在傅立叶域快速傅立叶变换（Fourier domain Fast Fourier Transform，FFT）[15]中计算相关性。首先，计算输入图像的2D傅里叶变换：\(F=f(\text{f})\) 以及滤波器的2D傅里叶变换：\(H =f(\text{h})\)。 卷积定理指出，相关性在傅立叶域中变成了元素乘法（函数互相关的傅里叶变换等于函数傅里叶变换的乘积）。 使用\(\odot\)符号表示逐元素乘乘法，使用*表示复共轭，那么相关性计算求解可以表示为以下形式：

\[G=F\bigodot H^* \tag{1} \]

使用逆FFT将相关输出从频域转换回空间域。此过程的瓶颈是计算正向和逆向FFT，因此整个过程的上限时间为O(PlogP)，其中P是跟踪窗口中的像素数。

在本节中，我们讨论基于过滤器的跟踪器的组件。3.1节讨论了在跟踪窗口上执行的预处理。3.2节介绍了MOSSE滤波器，这是从少量图像构造稳定的相关滤波器的改进方法。3.3节显示了如何使用正则化来产生更稳定的UMACE和ASEF过滤器。3.4节讨论了用于过滤器在线更新的简单策略。

3.1 预处理

FFT卷积算法的一个问题是图像和滤波器被映射到一个圆环状的拓扑结构。 换句话说，它将图像的左边缘连接到右边缘，并将顶部连接到底部。在卷积过程中，图像旋转通过环形空间，而不是像在空间域中那样平移。人工连接图像边界会引入影响相关输出的伪影。

通过遵循[3]中概述的预处理步骤，可以减少这种影响。

• 首先，使用 对数函数 对像素值进行转换，这有助于解决低对比度照明情况。像素值被归一化为平均值为0.0，范数为1.0。
• 最后，将图像乘以一个 余弦窗口，该余弦窗口 将边缘附近的像素值逐渐减小为零。这还有一个好处，就是 可以将更多的重点放在目标的中心附近。

3.2 MOSSE滤波器

MOSSE是一种用于从更少的训练图像中生成类似于ASEF的过滤器的算法。 首先，它需要一组训练图像\(f_i\)和训练输出\(g_i\)。 通常，\(g_i\)可以是任何形状。在这种情况下，\(g_i\)是由ground truth况生成的，因此它具有一个紧凑的（σ=2.0）2D高斯形状的峰，其中心位于训练图像\(f_i\)中的目标上。 训练在傅立叶域中进行，以利用输入和输出之间简单的元素关系。 如上一节所述，我们将大写的变量\(F_i\)，\(G_i\)和过滤器\(H\)定义为\(f_i\),\(g_i\),\(h\)经过傅里叶变换后的结果。

\[ H^*_i = \frac{G^i}{F^i} \tag{2} \]

其中除法为逐像素除法。

为了找到一个将训练输入映射到期望的训练输出的滤波器，MOSSE寻找并选择一个能够使卷积的实际输出和卷积的期望输出之间的平方误差之和最小的滤波器\(H\)。 此最小化问题的表示形式为：

\[\min_i\sum_i|F_i\bigodot H^* - G_i|^2 \tag{3} \]

最小化输出平方误差和（SSE）的想法并不新鲜。实际上，上述公式中的优化问题与[10]和[12]中提出的优化问题几乎相同。 不同之处在于，在那些论文中，假定目标始终始终以\(f_i\)为中心，并且输出（\(g_i\)）在整个训练集中都是固定的，而自定义每个\(g_i\)是ASEF和MOSSE背后的基本思想。在跟踪问题中，目标并不总是居中，而\(g_i\)中的峰值将跟随\(f_i\)中的目标。 在更一般的情况下，\(g_i\)可以具有任何形状。 例如，在[4]中，\(f_i\)中包含多个目标，\(g_i\)具有多个对应的峰。

解决此优化问题并不特别困难，但需要格外小心，因为要优化的函数是复杂变量的实值函数。 首先，H的每个元素（ω和ν分别表示横纵坐标索引）可以独立求解，因为傅里叶域中的所有运算都是逐元素执行的。 这涉及根据\(H_{ων}\)和\(H^*_{ων}\)重写函数。 然后，求解关于\(H_{ων}\)的偏导，令其为零，其中\(H_{ων}\)为自变量[13]。

\[0 = \frac{\partial}{\partial{H_{wv}^*}}\sum_i|F_{iwv}*H_{wv}^*-G_{iwv}|^2 \tag{4} \]

通过求解\(H^*\)，可以找到MOSSE滤波器的闭式解：

\[H^* = \frac{\sum_i G_i^* \bigodot F_i^*}{\sum_i F_i \bigodot F_i^*} \tag{5} \]

完整的推导在附录A中。公式5中的术语具有有趣的解释。 分子是输入与期望输出之间的相关性，分母是输入的能谱。

从公式5，我们可以发现UMACE是MOSSE的特例。 UMACE定义为\(H ^* = D^{-1}m^*\)，其中m是包含平均中心裁剪的训练图像的FFT的向量，D是包含训练图像的平均能谱的对角矩阵[18]。因为D是对角矩阵，所以乘以它的逆实际上就是执行逐元素的除法。 用当前的符号重写时，UMACE采用以下形式：

\[H^* = \frac{\sum_i F_i^*}{\sum_i F_i \bigodot F_i^*} \tag{6} \]

但是，UMACE要求目标必须以\(F_i\)为中心。可以使用相关性执行重新居中。如果我们将\(g_i\)定义为Kronecker增量（在目标中心的峰值为1，在其他位置的峰值为0），则这实际上将使目标更新并计算UMACE滤波器。该实现与传统实现之间的区别在于，这里我们先进行裁剪然后转换，而传统方法先进行转换然后进行裁剪。

为了显示MOSSE能产生比ASEF更好的滤波器，我们进行了一项实验，该实验改变了用于训练滤波器的图像数量。通过将随机的小型仿射扰动应用于视频第一帧的跟踪窗口来初始化滤波器。 第二帧的PSR用作滤波器质量的度量。图3显示，当在少量图像窗口上训练时，MOSSE会产生更好的滤波器。原因将在下一节中讨论。

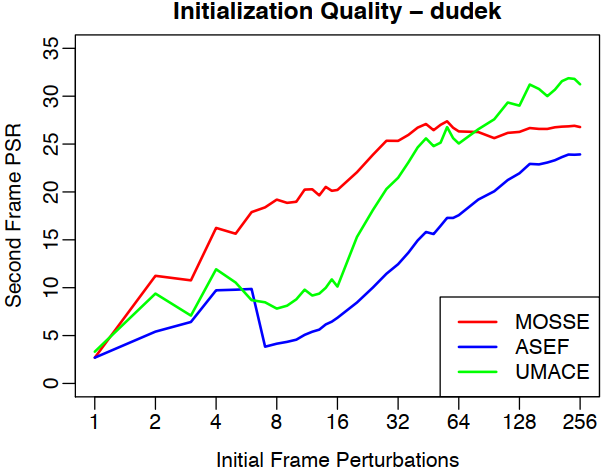
图3： 未正则化的结果。 横坐标：初始帧扰动， 纵坐标：下一帧的PSR(一种评价指标)

3.3 ASEF的正则化

ASEF采用略有不同的方法来最小化相关变换中的错误。 事实证明，当只有一个训练图像\(F_i\)和一个输出图像\(G_i\)时，存在一个产生零误差的滤波器。该过滤器称为精确过滤器，可以通过求解公式(1)来找到：

\[H_i^* = \frac{G_i}{F_i} = \frac{G_i\bigodot F_i^*}{F_i\bigodot F_i^*} \tag{7} \]

在一张图像上训练的精确滤波器几乎总是适合该图像。 但是当应用于新图像时，该过滤器通常会失败。平均处理(Averaging)用于产生更通用的滤波器。 进行平均的动机来自Bootstrap聚合[5]，在其中可以对弱分类器的输出进行平均以产生更强的分类器。通过一些操作，ASEF滤波器的公式可以显示为】：

\[H^* = \frac{1}{N}\frac{G_i \bigodot F_i^*}{F_i \bigodot F_i^*} \tag{8} \]

如果仅用一张图像进行训练，MOSSE和ASEF都生成一个精确的滤波器。

当在少量图像上训练时，ASEF滤波器不稳定，因为当训练图像中的频率包含很少的能量（或分母接近零）时，公式（8）中的按元素划分将变得不稳定。 平均大量的精确过滤器可弥补此问题，并产生可靠的ASEF过滤器。 由于MOSSE的分母是更多图像上能量的总和，因此它很少产生小数，因此更稳定。

相应地，可以使用正则化来校正低能量频率并产生更稳定的ASEF滤波器。这是通过将一个较小的值添加到能量谱中的每个元素上来执行的。 \(F_i\bigodot F_i ^∗\)替换为\(F_i\bigodot F_i ^∗+\epsilon\)，其中\(\epsilon\)是正则化参数。

正则化类似于通常与UMACE滤波器结合使用的OTF理论得出的结果。 该结果表明，将背景噪声的能谱添加到训练图像的能谱中将产生具有更好的噪声容忍度的滤波器[16]。 在这里，我们基本上增加了白噪声。

图4显示了调整\(\epsilon\)的效果。 通过适当的正则化，所有滤波器都会产生良好的峰值，并且应该足够稳定以产生良好的轨道。

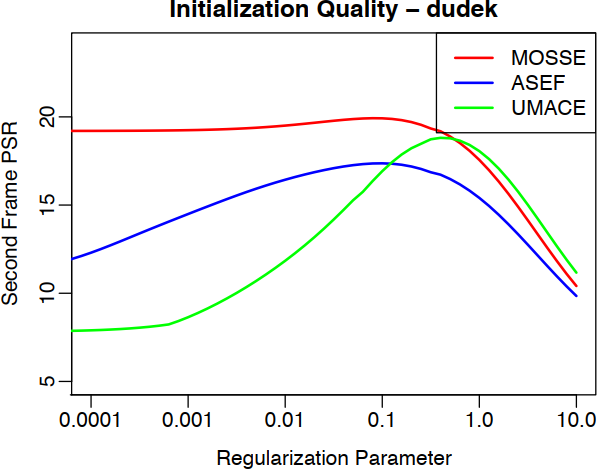
图4：在此图中，在调整正则化参数的同时，使用相同的八张图像初始化了所有三个滤波器。 在 \(\epsilon\)≈0.1时，所有三个滤波器均具有较高的PSR。

3.4 滤波器初始化以及在线训练

公式(8)和(5)描述了初始化期间如何构造滤波器。 使用随机仿射变换构造训练集，以在初始帧中生成跟踪窗口的八个小扰动（\(f_i\)）。还会生成训练输出（\(g_i\)），其峰值对应于目标中心。

在跟踪过程中，目标通常可以通过旋转，更改其比例，姿势，在不同的光照条件下移动甚至经历非刚性变形来更改外观。因此，滤波器需要快速适应以跟随对象。运行平均值用于此目的。例如，从第i帧获悉的ASEF过滤器的计算公式为：

\[H^*_i= = \eta \frac{G_i \bigodot F_i^* }{F_i\bigodot F_i^*} + (1-\eta)H^*_{i-1} \tag{9} \]

MOSSE滤波器为：

\[H^*_i = \frac{A_i}{B_i} \\ A_i = \eta G_i \bigodot F_i^* + (1-\eta)A_{i-1}\\ B_i = \eta F_i \bigodot F_i^* + (1-\eta)B_{i-1} \tag{10} \]

其中\(\eta\)是学习率。这使得更多的权重被放在最近的帧上，而先前帧对当前的影响效果随时间呈指数衰减。在实践中，我们发现\(\eta=0.125\)可使滤波器快速适应外观变化，同时仍保持滤波器的鲁棒性。

3.5 错误检测以及PSR

如前所述，对峰值强度的一种简单测量方法为“Peak to Sidelobe Ratio”（PSR）。为了计算PSR，将相关性输出g分为两部分：峰值和旁瓣，峰值即为最大值，旁瓣是峰值周围的11×11窗口内，除峰值以外的其余像素。然后将PSR定义为\(\frac{g_{max}-\mu_{sl}}{\sigma_{sl}}\)，其中\(g_{max}\)是峰值，而\(\mu_{sl}\)和\(\sigma_{sl}\)是旁瓣的平均值和标准差。

根据我们的经验，在正常跟踪条件下，用于UMACE，ASEF和MOSSE的PSR通常在20.0至60.0之间，这表示非常强的峰值。我们发现，当PSR降至7.0左右时，表明该对象被遮挡或跟踪失败。 对于朴素的实施(最一般的方法)，PSR的范围是3.0到10.0，对于预测轨道质量没有用。

4. 测试

最初，基于网络摄像头的实时视频创建并评估了基于MOSSE的实时跟踪系统。 实时反馈使测试跟踪器配置的细微变化以及对各种目标和跟踪条件的跟踪器性能进行定性分析更加容易。这些测试为跟踪器的操作提供了宝贵的见解，并有助于生成本文中介绍的快速而强大的跟踪器。

七个测试视频来源于数据集地址。这些视频都是灰度的，并且在光照，姿势和外观上都具有挑战性。存在摄像机运动，这增加了目标的不稳定运动。 这七个序列包括car4，car11，fish，sylv，davidin300，dudek和trellis70。

4.1 滤波器比较

本部分评估UMACE，ASEF和MOSSE滤波器的跟踪质量。将这些与朴素滤波器进行比较，该滤波器基于在线更新的平均预处理跟踪窗口。跟踪输出被手动标记为良好跟踪、偏离中心的跟踪或跟踪失败（请参见图5）。

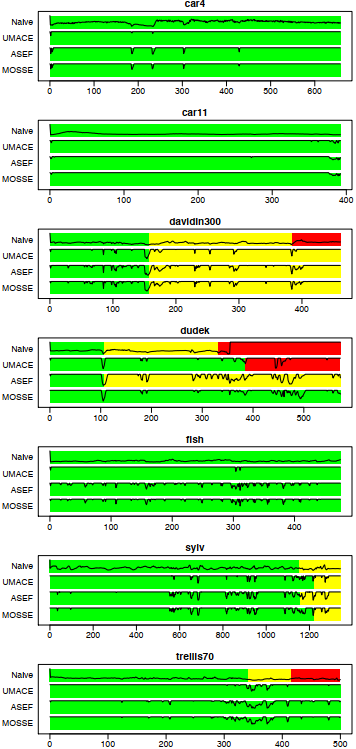
图5：此图显示了在所有七个视频序列上基于滤波器的跟踪器的性能。 每个输出视频都带有手动注释，其中绿色表示跟踪良好，黄色表示跟踪偏离中心，红色表示跟踪失败。黑线表示将PSR剪切到[0,20]范围，并表示视频每一帧的跟踪质量。

定性实验表明，包括朴素滤波器在内的所有滤波器，在对象存在比例变化，旋转以及光照变化时，都能够以很小的漂移定位到目标。但是当目标发生超出画面之外的大面积旋转时（非平面旋转），窗口大漂移和故障就会发生。比如图6中展示的有关davidin300序列的测试结果。滤波器倾向于跟踪目标中心的一个点。当旋转目标时，该点将移向目标边界，并且跟踪器最终处于大部分跟踪窗口被背景覆盖的状态。滤波器会适应这半个背景窗口，并且当目标旋转回正面姿势时移至新位置，否则它们可能会丢失目标，反而跟踪背景。

图6：非平面旋转（Out-of-plain rotation）引起的漂移示例.

这些结果表明，优化过的相关滤波器比朴素滤波器跟踪目标的时间更长。尖锐的峰值还说明了PSR可以很好地预测轨道质量，而PSR对于朴素滤波器不是特别有用。对于高级滤波器，漂移和故障总是与低PSR关联。如图7所示，该图表明MOSSE PSR可以定位该视频中最具挑战性的部分。

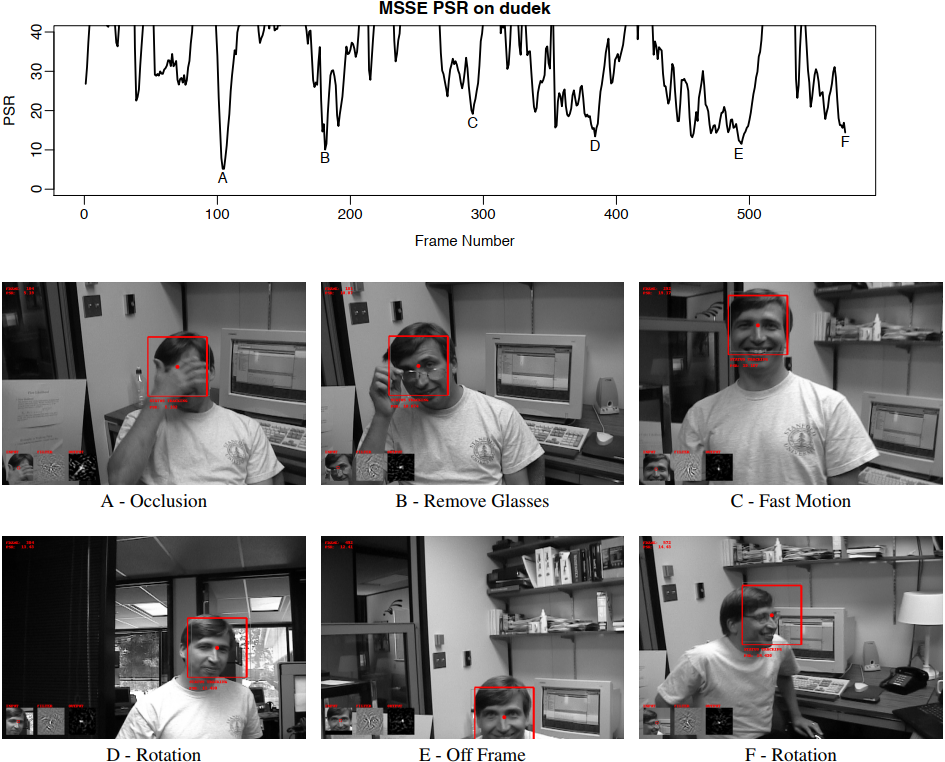
该图表明，可以通过在PSR中找到低点来定位视频中最具挑战性的部分。

对于基于滤波器的跟踪器，很难断言任何一种滤波器类型比其他的好。在四个测试视频上，相关滤波器都表现出色。在davidin300上，当发生平面外旋转时，所有滤波器都发生了从脸部中心到眼睛的漂移。在sylv中，所有滤波器在都在该序列最难的一段上发生漂移。这说明滤波器类型的选择不是特别重要，因为滤波器发生故障的方式完全相同。

仅在dudek序列上，三个滤波器之间才存在显着差异。只有MOSSE完美地完成了序目标跟踪，而UMACE和ASEF在挑战视频的部分时遇到了问题。但是，即使第3节中提供的证据表明MOSSE可能是完成此任务的最佳滤波器，但仅在一个视频序列上的单个故障不足以支持这一定论。因此还需要更多的研究。

4.3 实时性

基于滤波器的跟踪算法，其计算复杂度为O(PlogP)，其中P是滤波器中像素的数量。 这时因为在相关性计算以及在线更新过程中采用了快速傅里叶变化（FFT）。跟踪初始化会产生一次O(NPlogP)的成本，其中N是用于初始化第一个滤波器的仿射扰动数。尽管这比在线更新慢很多倍，但初始化仍比实时快，每秒更新66.32。

5. 结论

本文表明，在视觉跟踪领域，完全可以用轻量级的相关滤波器算法来替代传统的高权重分类器，复杂外观模型以及随机搜索技术。这不仅易于实现，而且精度高，速度快。

在本文中，跟踪器的保持操作简单，可以评估滤波器的跟踪能力并适应困难的跟踪情况。有很多简单的方法可以改进此跟踪器。 例如，如果目标的外观相对稳定，则可以通过偶尔基于初始帧重新设置滤波器来减轻漂移。跟踪器还可以扩展为通过在更新后过滤跟踪窗口的对数极坐标变换来估计比例和旋转的变化。

> 代码部分

% get images from source directory
datadir = '../data/';
dataset = 'Surfer';
path = [datadir dataset];
img_path = [path '/img/'];
D = dir([img_path, '*.jpg']);
seq_len = length(D(not([D.isdir])));
if exist([img_path num2str(1, '%04i.jpg')], 'file')
    img_files = num2str((1:seq_len)', [img_path '%04i.jpg']);
else
    error('No image files found in the directory.');
end

% select target from first frame
im = imread(img_files(1,:));
f = figure('Name', 'Select object to track'); imshow(im);
rect = getrect; % 得到的是矩形框的左上角坐标以及长和宽
close(f); clear f;
center = [rect(2)+rect(4)/2 rect(1)+rect(3)/2];

% plot gaussian
sigma = 100;
gsize = size(im);
[R,C] = ndgrid(1:gsize(1), 1:gsize(2)); % 产生两个m行，n列的矩阵，其中R第一列为1，暗猎递增
g = gaussC(R,C, sigma, center);
g = mat2gray(g);

% randomly warp original image to create training set 生成训练集
if (size(im,3) == 3) 
    img = rgb2gray(im); 
end
img = imcrop(img, rect); % 框出来的目标区域
g = imcrop(g, rect); % 目标区域对应的高斯掩膜
G = fft2(g); % 傅里叶变换,初始化滤波器
height = size(g,1);
width = size(g,2);
fi = preprocess(imresize(img, [height width]));
Ai = (G.*conj(fft2(fi))); % Gi*Fi* 
Bi = (fft2(fi).*conj(fft2(fi))); % Fi*Fi*
N = 128;
for i = 1:N
    fi = preprocess(rand_warp(img));
    Ai = Ai + (G.*conj(fft2(fi)));
    Bi = Bi + (fft2(fi).*conj(fft2(fi)));
end

% MOSSE online training regimen
eta = 0.125;
fig = figure('Name', 'MOSSE');
mkdir(['results_' dataset]);
for i = 1:size(img_files, 1)
    img = imread(img_files(i,:));
    im = img;
    if (size(img,3) == 3)
        img = rgb2gray(img);
    end
    if (i == 1)
        Ai = eta.*Ai;
        Bi = eta.*Bi;
    else
        Hi = Ai./Bi;
        fi = imcrop(img, rect); 
        fi = preprocess(imresize(fi, [height width]));
        gi = uint8(255*mat2gray(ifft2(Hi.*fft2(fi))));
        maxval = max(gi(:)); 
        [P, Q] = find(gi == maxval); % 可能有多个峰值，取均值
        dx = mean(P)-height/2; % 重新求解新中心坐标位置
        dy = mean(Q)-width/2;
        
        rect = [rect(1)+dy rect(2)+dx width height];
        fi = imcrop(img, rect); 
        fi = preprocess(imresize(fi, [height width]));
        Ai = eta.*(G.*conj(fft2(fi))) + (1-eta).*Ai; % 论文公式(10)
        Bi = eta.*(fft2(fi).*conj(fft2(fi))) + (1-eta).*Bi;
    end
    
    % visualization 可视化
    text_str = ['Frame: ' num2str(i)];
    box_color = 'green';
    position=[1 1];
    result = insertText(im, position,text_str,'FontSize',15,'BoxColor',...
                     box_color,'BoxOpacity',0.4,'TextColor','white');
    result = insertShape(result, 'Rectangle', rect, 'LineWidth', 3);
    imwrite(result, ['results_' dataset num2str(i, '/%04i.jpg')]);
    imshow(result);
end

总结：

why work?

• 条件滤波器 + 傅里叶域求解：加速
• 更新策略，采用程度因子\(\eta\)把控更新程度