CF830E Perpetual Motion Machine 题解
前言
好久没写博了2333
逛 CF 的时候翻到一道数学好题,就想来写写
题意
给定 $n$ 个点 $m$ 条边的图,你可以给每个点赋上一个不大于 $0$ 的点权,每个点将产生点权的平方的花费,每条边将产生连接两点的点权乘积的贡献,问是否存在一种方案使得贡献之和 $\ge$ 花费之和且至少一点的点权不为 $0$ 。无重边无自环。
题解
首先,如果图有环,则显然把这个环上的点权全部赋成相等的数就行了。
那么只剩下图是一个森林的情况,我们对这个森林中的每颗树单独考虑:
- 如果有一个点的度数大等于 $4$ ,则把这个点赋值为 $2$ ,与它相邻的点赋为 $1$,产生的贡献-花费为 $2 \times du_x - 2*2 - du_x = du_x - 4 \le 0$;
- 如果有两个点的度数等于 $3$,则把这两点间路径上的点(包括这两点)设为 $2$,与这两点相连的其他点设为 $1$,产生的贡献-花费为 $du_x - 1 + du_y - 1 - 4 \le 0$;
- 如果只有一个点的度数等于 $3$,则该树为一个点连着三条链,设这三条链长度(不包括链头的度数为 $3$ 的那个点)分别为 $x, y, z$ ,若 $ \frac{1}{x+1} + \frac{1}{y+1} + \frac{1}{z+1} \le 1$ 有解(构造方式在下面给出),否则无解
- 如果没有一个点的读书大于 $2$,既该树为一条链,则该联通块无解。
对于前两种情况很显然,但如果是后两种情况呢?
证明
假设我们现在已经确定了某条链除叶子结点外其余所有点的权值,现要确定叶子节点的权值,如何确定才能使该叶子结点产生的收益最大?
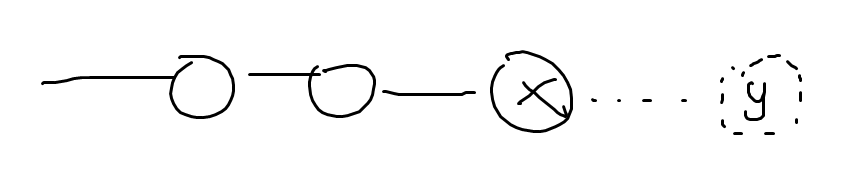
不妨设叶子节点的权值为 $y$,与叶子结点相连的权值为 $x$,$f_{a,b}$ 表示将长度为 $b$ 的一串链接到某条末尾结点权值为 $a$ 的链之后产生收益;
则产生的收益为 $f_{x,1} = x \times y - y \times y = (x - y) \times y$;
很显然的均值不等式:$\sqrt{(x - y) \times y} \le \frac{x}{2}$,当且仅当 $x - y = y$ 的时候等号成立
所以 $y$ 要取 $\frac{x}{2}$ 的时候,$f_{x,1}$ 取到最大值 $\frac{x^2}{4}$。
那么如果是要接两个结点呢?
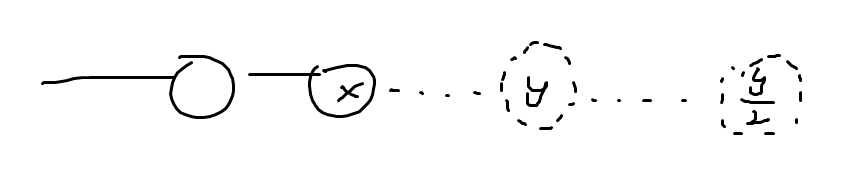
$f_{x,2} = x \times y - y \times y + f_{y,1} \le x \times y - y \times y + \frac{y^2}{4} = - \frac{3}{4}y^2 + xy$;
将 $x$ 视为系数,则为二次函数极值:当 $y = - \frac{x}{2 \times (- \frac{3}{4})} = \frac{2}{3}x$ 时,$f_{x,2}$ 取到最大值 $\frac{x^2}{3}$
还没发现规律?
- 当 $y = \frac{3}{4}$ 时,$f_{x,3}$ 取到最大值 $ \frac{3}{8} x^2$;
- 当 $y = \frac{4}{5}$ 时,$f_{x,4}$ 取到最大值 $ \frac{2}{5} x^2$;
- $\cdots$
我们发现,似乎一条长度为 $i$ 的链接到权值为 $x$ 的最大收益是从叶子结点依次取权值 $y, 2y, 3y \cdots iy$,其中 $ (i + 1)y = x$;
尝试用归纳法证明这个东西
假定对于长度为 $i$ 的链满足以上性质,我们要证明长度为 $i + 1$ 的链也满足该性质:
$Max\left \{f_{(i+1)y, i}\right \} = \sum_{j=1}^{i} ((j+1)y \times jy - jy \times jy) = \sum_{j=1}^{i} jy^2 = \frac{(1 + i) \times i}{2} y^2$
则 $Max \left \{f_{x, i + 1}\right \} = (i+1)y \times x - (i+1)y \times (i+1)y + Max\left \{f_{(i+1)y, i}\right \} = - (1 + i) \times (\frac{i}{2} + 1) \times y^2+ (i + 1)y \times x$
当 $y = - \frac{(i + 1)x}{- 2(1 + i)} \times (\frac{i}{2} + 1) = \frac{x}{i + 2}$ 时,$f_{x, i+1}$ 最大;
得证
所以对一条长度为 $len$ 的链,他的最大收益为 $Max \left \{f_{x, len}\right \} = \frac{i}{2 \times (i+1)} x^2$;
对于第 $4$ 种情况,全图的总最大收益为 $\frac{n - 1}{2 \times n} x^2 - x^2 < 0$,无解;
对于第 $3$ 种情况,设度数为 $3$ 的点权为 $v$,则最大收益为 $\frac{x}{2 \times (x+1)} v^2 + \frac{y}{2 \times (y+1)} v^2 + \frac{z}{2 \times (z+1)} v^2 - v^2 $ ;
要使其大等于 $0$ ,则 $\frac{x}{2 \times (x+1)} + \frac{y}{2 \times (y+1)} + \frac{z}{2 \times (z+1)} \geq 1$;
整理下即 $ \frac{1}{x+1} + \frac{1}{y+1} + \frac{1}{z+1} \le 1$;
显然,我们基于以上证明很容易想到一种顶点取 $lcm(x + 1, y + 1, z + 1)$,然后每条链单独成比例构造下来的构造方式;但这会超过题目要求的点权在 $10^6$ 内的限制,所以我们考虑以下构造方式(不妨设 $x \ge y \ge z$):
- 若 $z \ge 2$,我们取顶点为 $3$,每条链与根相邻那端分别取 $2$ 和 $1$ ,其余取 $0$ ;
- 若 $z = 1, y \ge 3$,则取顶点为 $4$,$z$ 链取 $2$,$y , z$ 相邻那端分别取 $3, 2, 1$;
- 其余情况就取 $(x + 1) \times (y + 1) \times (z + 1)$,然后成比例构造下来即可,此时 $(x + 1) \times (y + 1) \times (z + 1) \le 6(x + 1) \le 6 \times 10^5 < 10^6$
代码实现

#include<bits/stdc++.h> #define MN 100005 int n,m,t,cnt,h[MN],ans[MN],X,siz[MN],fa[MN],id[3],du[MN]; bool vis[MN],ok,v2[MN]; struct edge{ int to,nxt; }e[MN<<1]; void ins(int x,int y) { e[++cnt].nxt=h[x];h[x]=cnt;e[cnt].to=y; du[x]++; } void dfs(int x,int f) { fa[x]=f; vis[x]=1; for(int i=h[x];i;i=e[i].nxt) if(e[i].to!=f) { if(vis[e[i].to]) { ok=1; for(;1;x=fa[x]) { ans[x]=1; if(x==e[i].to) break; } return; } dfs(e[i].to,x); if(ok) return; } if(du[x]>3) { for(int i=h[x];i;i=e[i].nxt) ans[e[i].to]=1; ans[x]=2; ok=1; return; } if(du[x]==3) { if(X) { for(int i=h[x];i;i=e[i].nxt) ans[e[i].to]=1; for(int i=h[X];i;i=e[i].nxt) ans[e[i].to]=1; int y=x; for(;x;x=fa[x]) v2[x]=1; for(;X;X=fa[X]) { ans[X]=2; if(v2[X]) break; } for(;y!=X;y=fa[y]) ans[y]=2; ok=1; return; } X=x; } } void calc(int x,int f) { siz[x]=1; for(int i=h[x];i;i=e[i].nxt) if(e[i].to!=f) { calc(e[i].to,x); siz[x]+=siz[e[i].to]; } } void get(int x,int f) { if(!ans[f]) ans[x]=0; else ans[x]=ans[f]/(siz[x]+1)*siz[x]; for(int i=h[x];i;i=e[i].nxt) if(e[i].to!=f) { siz[e[i].to]=siz[x]-1; get(e[i].to,x); } } int main() { for(scanf("%d",&t);t--;) { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) h[i]=ans[i]=siz[i]=du[i]=0; for(int i=1;i<=n;i++) vis[i]=v2[i]=0; cnt=ok=0; for(int x,y;m--;) { scanf("%d%d",&x,&y); ins(x,y); ins(y,x); } for(int i=1;i<=n;i++) if(!vis[i]) { X=0; dfs(i,0); if(ok) break; if(!X) continue; for(int j=h[X],k=0;j;j=e[j].nxt,k++){calc(e[j].to,X);id[k]=e[j].to;} for(int j=0;j<3;j++) for(int k=j+1;k<3;k++) if(siz[id[j]]>siz[id[k]]) std::swap(id[j],id[k]); int xx=siz[id[0]]+1,yy=siz[id[1]]+1,zz=siz[id[2]]+1; if(1ll*xx*yy+1ll*yy*zz+1ll*xx*zz>1ll*xx*yy*zz) continue; if(xx>=3) ans[X]=3,siz[id[0]]=siz[id[1]]=siz[id[2]]=2; else if(yy>=4) ans[X]=4,siz[id[1]]=siz[id[2]]=3; else ans[X]=xx*yy*zz; for(int j=0;j<3;j++) get(id[j],X); ok=1; break; } if(ok) { puts("YES"); for(int i=1;i<=n;i++) printf("%d ",ans[i]);puts(""); } else puts("NO"); } }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号