hdu4859 (最大流最小割)
中文题面不再复述。首先来讲下什么是最小割,假设去掉(割掉)一些边使得一个图不再连通,这些边有很多种删去方法,但每条边都有一个权值(或者说容量),使得这些所有删去的边的容量和最小的情况就称作最小割。学习过最大流可以发现,最大流是取每条增广路上可通过的最大流量,因此最大流量和刚好和最小割取得的容量和相等。题目抽象为模型可知,'E'可看作'.',也可看作'D',假设我们直接套用最大流模板建图,将所有的'.'与源点s相连,将所有的'D'与汇点相连,那么情况如下图:
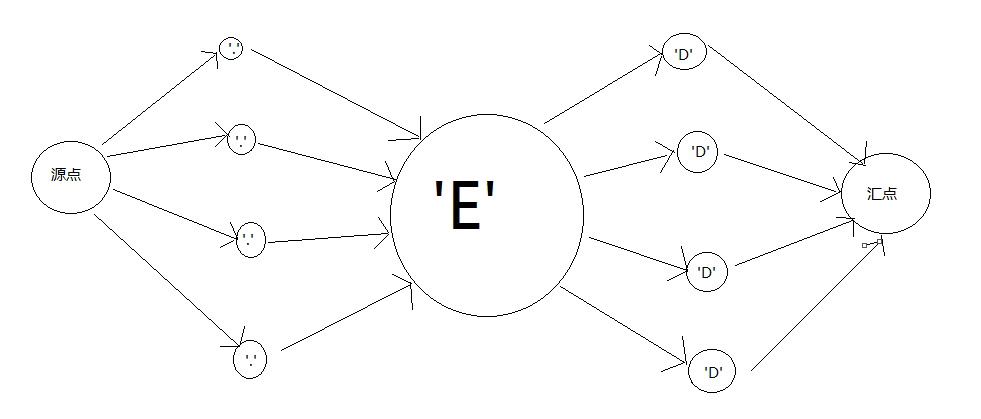
如果照上图建图,我们得到的是最小的'.'和'D'相连的数目(即最小海岸线)。然而题上要求的求最长的海岸线。一开始怎么想都不理解怎么转化建模。我们想要求最长的海岸线,就是求最大的'.'和'D'可相邻数,换句话说,就是最小的'.'或'D'相同相邻数。这里介绍一种较为神奇的模型构造法,奇偶建图。由于我们建图时会把相邻的点连接在一起,那么相连的点必然是一奇一偶,为了与这种情况相匹配,我们可以图上的点(i,j)i+j为奇数的'.'与源点s相连,i+j为偶数的'D'与源点相连,i+j为偶数的'D'和i+j为奇数的'D'与汇点相连。这样建图后,源点的'.'对应的汇点连接的至少不会是'D'(因为奇数连接的会是偶数,偶数连接的会是奇数),这样进行最大流最小割求解,得到的刚好就是最少的相同字符的可相邻数,这样我们用恒定不变的总相邻数减去最少相同字符的可相邻数,便可得到最大不同字符相邻数了,即题上要求的最长海岸线。总相邻数可在建图的时候就进行统计。需要注意数据范围,尽管图只有47*47这么大,但是我们需要对外界圈一圈边界也算作海岸线,因此点的范围要到2500的样子。思路明确,具体实现细节看代码。

#include <stdio.h> #include <algorithm> #include <string.h> #include <queue> using namespace std; #define oo 0x3f3f3f3f struct ad { int v, next, flow; } edge[3000000]; int head[3000], edge_num, id[110][110], vis[3000]; int dir[4][2] = { {0, 1}, {0, -1}, {1, 0}, {-1, 0} }; char maps[110][110]; void Init() { memset(head, -1, sizeof(head)); memset(maps, 0, sizeof(maps)); edge_num = 0; } void Add(int x, int y, int flow) { edge[edge_num].flow = flow; edge[edge_num].next = head[x]; edge[edge_num].v = y; head[x] = edge_num++; edge[edge_num].flow = 0; edge[edge_num].v = x; edge[edge_num].next = head[y]; head[y] = edge_num++; } bool bfs(int start, int over) { queue<int>Q; Q.push(start); memset(vis, 0, sizeof(vis)); vis[start] = 1; while(!Q.empty()) { int now = Q.front(); Q.pop(); if(now == over) return true; for(int i=head[now]; i!=-1; i=edge[i].next) { int v = edge[i].v; if(!vis[v] && edge[i].flow>0) { vis[v] = vis[now]+1; Q.push(v); } } } return false; } int dfs(int u, int over, int Maxflow) { if(u == over) return Maxflow; int now_flow = 0; for(int i=head[u]; i!=-1; i=edge[i].next) { int v = edge[i].v; if(vis[v] == vis[u]+1 && edge[i].flow>0 && Maxflow-now_flow>0) { int flow = min(Maxflow-now_flow, edge[i].flow); flow = dfs(v, over, flow); edge[i].flow -= flow; edge[i^1].flow += flow; now_flow += flow; } } if(!now_flow) vis[u] = -1; return now_flow; } int dinic(int start, int over) { int ans = 0; while(bfs(start, over)) ans += dfs(start, over, oo); return ans; } int main() { int T, n, m, icase = 1; scanf("%d", &T); while(T--) { Init(); scanf("%d %d", &n, &m); for(int i=1; i<=n; i++) scanf("%s", maps[i]+1); int s = (n+2)*(m+2)+1, e = s + 1; for(int i=0; i<=n+1; i++) maps[i][0] = maps[i][m+1] = 'D'; for(int i=0; i<=m+1; i++) maps[0][i] = maps[n+1][i] = 'D'; int cnt = 0; for(int i=0; i<=n+1; i++) for(int j=0; j<=m+1; j++) id[i][j] = cnt++; cnt = 0; for(int i=0; i<=n+1; i++) for(int j=0; j<=m+1; j++) { for(int k=0; k<4; k++) { int dx = i+dir[k][0]; int dy = j+dir[k][1]; if(dx>=0 && dx<=n+1 && dy>=0 && dy<=m+1) { cnt++; Add(id[i][j], id[dx][dy], 1); } } if(maps[i][j] == 'E') continue; if(((i+j)%2==1 && maps[i][j]=='.') || ((i+j)%2==0 && maps[i][j]=='D')) Add(s, id[i][j], oo); else Add(id[i][j], e, oo); } printf("Case %d: %d\n", icase++, cnt/2-dinic(s, e)); } return 0; }




