三、词法分析

词法分析

• 词法分析基于正则文法进行的，即识别的单词是该类文法的句子
• 词法分析的任务是识别单词
• 单词：保留字、标识符、常数、运算符、分界符
• 标识符是语法概念，名字是语义概念

词法分析器

• 词法分析器用于识别单词
• 词法分析程序，接受输入的源程序，输出结果是单词的种别编码和单词的属性值
• 扫描器所完成的任务是从字符串形式的源程序中识别出一个个具有独立含义的最小语法单位即单词
• 词法分析器的结构：预处理子程序、扫描缓冲区、扫描器

有限自动机

确定的有限自动机 \(DFA(Deterministic ~\ Finite ~\ Automata)\)

非确定的有限自动机 \(NFA(Nondeterministic ~\ Finite ~\ Automata)\)

\(\star NFA\) 和 \(DFA\) 比较

• \(DFA\) 是 \(NFA\) 的特殊形式
• \(DFA\) 初态唯一，\(NFA\) 可以有多个初态
• \(DFA\) 和 \(NFA\) 都可以有多个接受状态(终态)
• \(DFA\) 的状态转换函数是单值映射，\(NFA\) 的状态转换函数是多值映射
• \(DFA\) 后继状态唯一，\(NFA\) 后继状态不一定唯一
• \(DFA\) 任何状态都没有 \(ε\) 转换，\(NFA\) 可以有 \(ε\) 转换

构造与某一正规式等价的DFA
解题步骤：

1. 根据正规式画出对应状态的状态转换图
2. 根据状态转换图画出对应状态转换矩阵
3. 根据状态转换矩阵得到重命名的状态转换矩阵 (子集构造算法)
4. 根据重命名状态转换矩阵得出 \(DFA\)

DFA化简(最小化)
解题步骤：

1. 划分终态组和非终态组
2. 若读入某个字符，得到的后继状态不在同一个集合里，就继续划分
3. 合并等价状态
4. 画出新的 \(DFA\)

题型

1. 设计正规式

给出下面正规式表达式

1. 以01结尾的二进制数串
   解：(0|1)*01
2. 能被5整除的十进制整数
   解：(1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)*(0|5)|(0|5)
3. 包含奇数个1或奇数个0的二进制数串
   解：0*1(0|10*1)*|1*0(1|01*0)*
4. 不包含子串abb的由a和b组成的符号串的全体
   解：b*(a|ab)*
5. 每个1都有0直接跟在右边
   解：(0|10)*

$\star\star\star$2. 正规式构造 \(NFA\) ，由 \(NFA\) 确定化为 \(DFA\) ，\(DFA\) 的化简

构造下列正规式相应的NFA，确定化为 \(DFA\) ，并且对 \(DFA\) 化简

1. 1(0∣1)*101
   解：
   \(NFA\) :
   

   状态转换矩阵：

   I	0	1
   {1}	\(\emptyset\)	{2}
   {2}	{2}	{2,3}
   {2,3}	{2,4}	{2,3}
   {2,4}	{2}	{2,3,5}
   {2,3,5}	{2,4}	{2,3}

   重命名后的状态转换矩阵：

   I	0	1
   A	\(\emptyset\)	B
   B	B	C
   C	D	C
   D	B	E
   E	D	C

   确定化后的 \(DFA\) ：
   
   1.非终态组：{A,B,C,D} ，终态组：{E}
   2.第一次划分：{A},{B,C,D},{E}
   3.第二次划分：{A},{B,C},{D},{E}
   4.第三次划分：{A},{B},{C},{D},{E}
   即 \(DFA\) 已经是最简
   化简后的 \(DFA\) ：
   

2. a*(b|a)(a|b)*ba
   解：
   \(NFA\) :
   

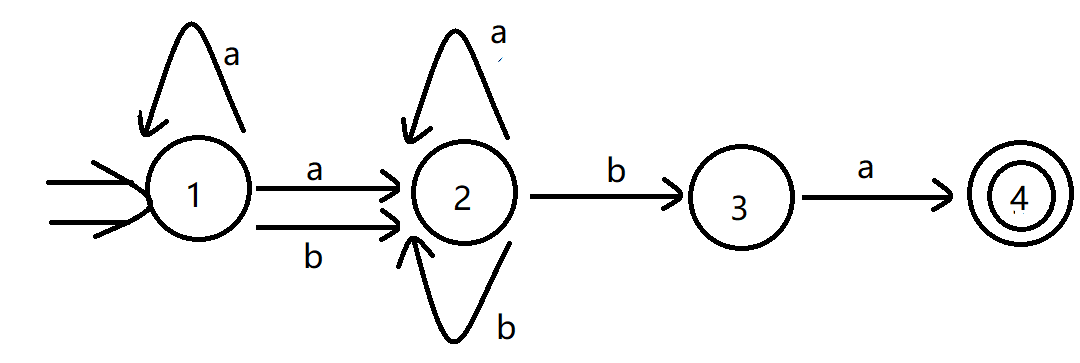
   状态转换矩阵：

   I	a	b
   {1}	{1,2}	{2}
   {1,2}	{1,2}	{2,3}
   {2}	{2}	{2,3}
   {2,3}	{2,4}	{2,3}
   {2,4}	{2}	{2,3}

   重命名后的状态转换矩阵：

   I	a	b
   A	B	C
   B	B	D
   C	C	D
   D	E	D
   E	C	D

   确定化后的 \(DFA\) ：
   

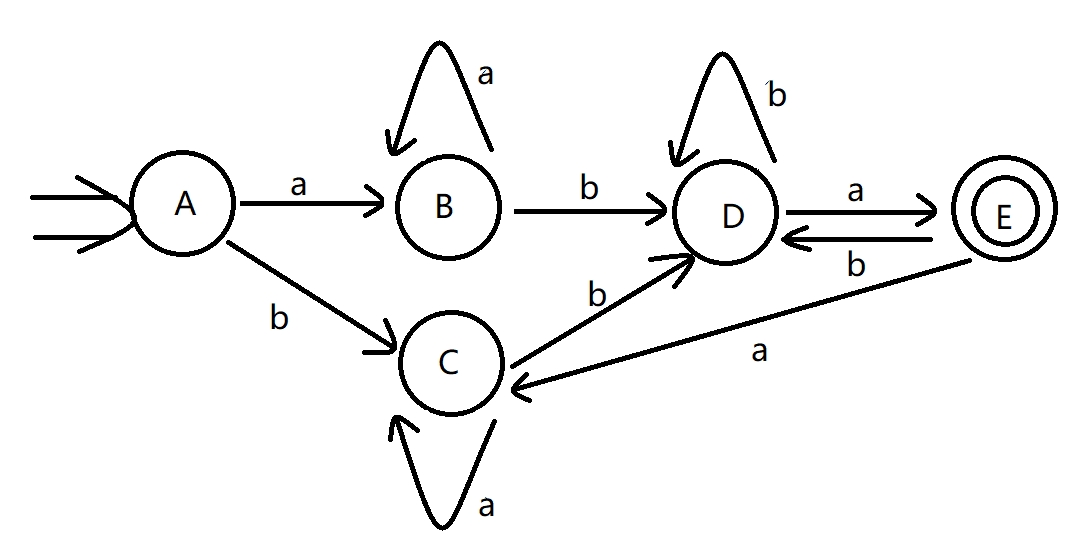
   1.非终态组：{A,B,C,D} ，终态组：{E}
   2.第一次划分：{A,B,C},{D},{E}
   3.第二次划分：{A},{B,C},{D},{E}
   重新命名为 A,B,C,D
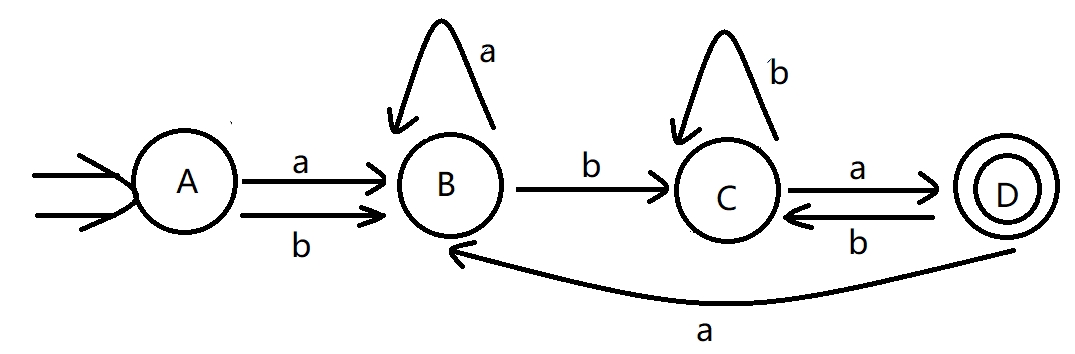
   化简后的状态转换矩阵：

   I	a	b
   A	B	B
   B	B	C
   C	D	C
   D	B	C

化简后的 \(DFA\) ：