二、高级语言语法描述

文法

上下文无关文法

\[\begin{align*} 文法 G[S]=(V_N，V_T，P，S)=> \left\{ \begin{aligned} V_N&:非终结符集合\\ V_T&:终结符集合\\ P&:产生式\\ S&:文法开始符号 \end{aligned} \right. \end{align*} \]

四种文法
0型 —— 短语文法
1型 —— 上下文有关文法
2型 —— 上下文无关文法
3型 —— 正则文法（\(A \rightarrow B\alpha|\alpha\) (左线性) 或 \(A \rightarrow \alpha B|\alpha\)(右线性)）

文法化简

1. 删除 \(P\rightarrow P\) 形式的产生式
2. 删除不能推导出终结符的产生式
3. 删除在推导中永不使用的产生式

基本概念

句型：从文法开始符号开始，每步推导所得到的字符串 (包括0步推导)
句子：仅含终结符的句型
二义性文法：文法中存在某个句子对应两棵不同的语法树，或两种不同的最左推导或两种不同的最右推导
最左推导：每次替换最左边非终结符
最右推导：每次替换最右边非终结符
直接推导：\(\Rightarrow\)
间接推导：

• 一步或多步推导：\(\stackrel{+}{\Rightarrow}\)
• 零步或多步推导：\(\stackrel{*}{\Rightarrow}\)
  
  

二义性

• 文法无二义，最左推导和最右推导语法树必定相同，推导未必相同
• 文法无二义，仅存在一个最左推导和一个最右推导
• 文法定义的语言是无限集，则文法必然是递归的

句柄

• 在规范规约中用句柄来刻画可归约串
• 语法无二义，句柄唯一
• 语法二义，句柄可能不唯一
• 句柄是该句型中一个和产生式右部匹配的子串

语法树

子树：任意节点及其全部后继
直接子树(树高为1)：一子树根只有直接后继
短语：每棵子树的叶子
直接短语：每棵直接子树的叶子
句柄：某句型的最左直接短语(规范分析中最先被规约的子串)
素短语：至少包含一个终结符且不包含更小素短语的短语

题型

1.根据文法描述语言

给出下列文法所描述的语言

1. \(S \rightarrow aSbS|bSaS|ε\)
   解：a的个数和b的个数相等的串的集合

2. \(S \rightarrow aAb \quad A \rightarrow cA|ε\)
   解：\(L(G)=\{ac^nb|n \ge 0 \}\)

2.根据语言设计文法

构造产生下列语言的文法

1. \(L(G)=\{a^n b^n|n \ge 0 \}\)
   解：
   \(G[S]:\)
   \(S\rightarrow aSb|ε\)
   
   
2. 设计一个文法，语言是正奇数集合，允许以0开头
   解：
   \(G[S]:\)
   \(S \rightarrow TA\)
   \(T \rightarrow TR|ε\)
   \(R \rightarrow 0|1|2|3|4|5|6|7|8|9\)
   \(A \rightarrow 1|3|5|7|9\)
   
   
3. 设计一个文法，语言是能被5整除的十进制数
   解：
   \(G[S]:\)
   \(S \rightarrow TR|R\)
   \(T \rightarrow TA\)
   \(A \rightarrow 0|1|2|3|4|5|6|7|8|9\)
   \(T \rightarrow 1|2|3|4|5|6|7|8|9\)
   \(R \rightarrow 0|5\)
   
   
4. 设计一个文法，语言是正偶数集合，不允许以0开头
   解：
   \(G[S]:\)
   \(S \rightarrow TR|B\)
   \(T \rightarrow TA\)
   \(T \rightarrow 1|2|3|4|5|6|7|8|9\)
   \(A \rightarrow 0|1|2|3|4|5|6|7|8|9\)
   \(R \rightarrow 0|2|4|6|8\)
   \(B \rightarrow 2|4|6|8\)

3.证明文法二义性

1. \(G[S]:S \rightarrow iSeS|iS|i\)
   解：
   
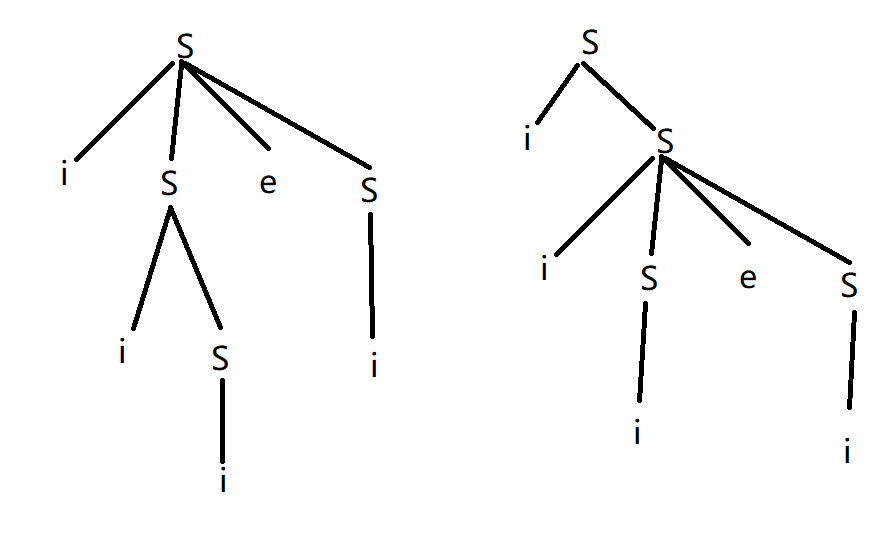
   句子 \(iiiei\) 对应两棵不同的语法树，故该文法是二义的
   
   

2. \(G[T]: T \rightarrow()|(T)|TT|ε\)
   解：
   

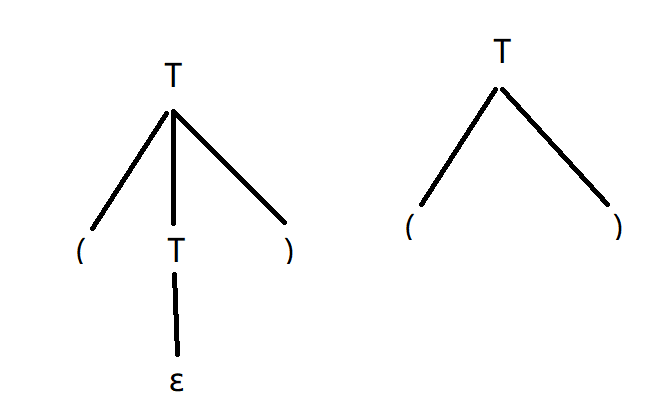
   句子 \(()\) 对应两棵不同的语法树，故该文法是二义的