Codeforces Round 867 (Div. 3)(A~D)

目录

• A. TubeTube Feed
  • 题意
  • 思路
  • 代码
• B. Karina and Array
  • 题意
  • 思路
  • 代码
• C. Bun Lover
  • 题意
  • 思路
  • 代码
• D. Super-Permutation
  • 题意
  • 思路
  • 代码

A. TubeTube Feed

题意

给定时间 \(t\) ,每个视频有一个价值 \(b_i\)，观看一个视频需要 \(a_i\) 秒，跳过一个视频需要花费\(1s\),求能观看完的价值最大的视频编号

思路

从前到后遍历即可，当 \(a_i\) 小于 \(t\)，并且 \(b_i\) 比当前价值 \(val\) 大时，更新答案

代码

#include<bits/stdc++.h>
using namespace std;

int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		int n,all;
		cin>>n>>all;
		vector<int>a(n+1),b(n+1);
		for(int i=1;i<=n;i++)
			cin>>a[i];
		
		for(int i=1;i<=n;i++)
			cin>>b[i];
		
		int val=-1;
		int id;
		for(int i=1;i<=n;i++)
		{
			if(a[i]<=all)
			{
				if(b[i]>val)
				{
					val=b[i];
					id=i;
				}
			}
			all--;
		}
		
		
		if(val==-1)puts("-1");
		else cout<<id<<endl;
	}
	return 0;
}

B. Karina and Array

题意

给定一个数组，数组中必须至少包含两个元素。你可以删除任意数量的元素（可能为零），求操作完后相邻元素的最大乘积可以是多少

思路

• 当正数和负数的个数 \(\geq 2\) 时， 答案为两种数字里，绝对值最大值和次大值的乘积取 \(max\) 。
• 当有一个正数一个负数时，如果有0存在，答案为0；否则答案为正数与负数的乘积

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		int n;
		cin>>n;
		vector<ll>a,b;
		
		bool flag=false;
		for(int i=0;i<n;i++)
		{
			ll x;
			cin>>x;
			if(x>0)a.push_back(x);
			else b.push_back(-x);
		}
	
		sort(a.begin(),a.end(),greater<ll>());
		sort(b.begin(),b.end(),greater<ll>());
		
		ll ans=-1e9;
		if(a.size()>=2)ans=max(ans,a[0]*a[1]);
		if(b.size()>=2)ans=max(ans,b[0]*b[1]);
		
		if(a.size()==1&&b.size()==1)
		{
			if(n>2)ans=0;
			else ans=-a[0]*b[0];
			
		}
		
	    cout<<ans<<endl;
	}
	return 0;
}

C. Bun Lover

题意

求深色边框的长度

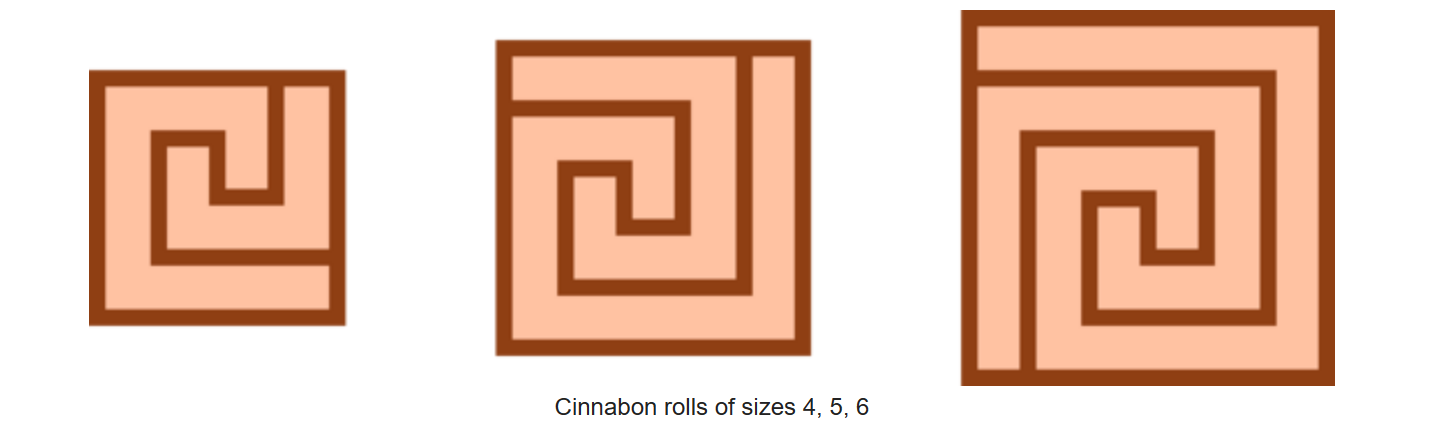
思路

观察图形猜结论，可以平移线段填补边框,推导出公式

发现当边长为 \(n\) ，长度 \(length+=n*4+i*2-(n-4) \quad [for\quad i \quad in \quad [2 \sim n-1]]\)
$ a_n=4,8,…,2n-2,S_n= \frac{(n-2)(4+(2n-2))}{2}=(n-2)*(n+1)$

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		ll n;
		cin>>n;
		
		ll res=n*4+(n-2)*(n+1);

		cout<<res-n+4<<endl;
	}
	
	return 0;
}

D. Super-Permutation

题意

设 \(b_i=(a_1+a_2+ … +a_i)\) ，问能否找到 \(1\sim n\) 的一个排列 \([a_1,a_2,…,a_n]\)，使得 $ [b_1+1,b_2+1,…,b_n+1]$ 也是\(1\sim n\) 的一个排列，若存在，输出 \([a_1,a_2,…,a_n]\)；否则输出\(-1\)

思路

• 当 \(n=1\) 时，答案显然为 \(1\)
• 当 \(n\gt 1\) 时， 假设 \(a_k= n\)，那么 \(b_k=(a_1+a_2+…+a_k) mod \ n=(b_{k-1}+n)mod \ n=b_{k-1}，k\) 只能取 \(1\)，否则 \(b\) 就不是一个排列，因此 \(a_1\) 必定为 \(n\)
  • 当 \(n\) 为奇数时，$ b_n=(a_1 + a_2 + … + a_n)mod \ n=(1+2+ … +n)mod n= \frac{n(n+1)}{2}mod \ n=0=b_1 $ ，\(b\) 中有重复的数字，无解
  • 当 \(n\) 为偶数时，根据样例，可以构造 \(a=[n,n-1,2,,n-3,4,…,n-i]\)
    • \(a[0]=0\)
    • 当 \(i\) 是奇数时 \(a[i]=n-i\)
    • 当 \(i\) 是偶数时 \(a[i]=i\)

代码

#include<bits/stdc++.h>
using namespace std;

int main()
{
	int T;
	cin>>T;
	
	while(T--)
	{
		int n;
		cin>>n;
		if(n==1)
		{
			puts("1");
			continue;
		}
		
		if(n%2==1)puts("-1");
		else{
			cout<<n<<' ';
			
			for(int i=1;i<=n-1;i++)
			{
				if(i%2==1)cout<<n-i<<' ';
				else cout<<i<<' ';
			}
			
			puts("");
		}
	}
	
	
	return 0;
}