通俗机器学习—朴素贝叶斯

引言 机器学习分类中的k近邻法和决策树师确定的分类算法，数据实例最终会被明确划分到某个分类中，本节我们讨论的分类算法将不能

完全确定数据实例应该划分到某个分类，或者智能给出数据实例属于给定分类的概率

 

一 朴素贝叶斯算法 

1. 简介

NaïveBayes算法，又叫朴素贝叶斯算法，朴素：特征条件独立；贝叶斯：基于贝叶斯定理。属于监督学习的生成模型，实现简单，没有迭代，并有坚实的数学理论（即贝叶斯定理）作为支撑。在大量样本下会有较好的表现，不适用于输入向量的特征条件有关联的场景。

2. 基本思想

 (1)病人分类的例子

 某个医院早上收了六个门诊病人，如下表：

 症状　　职业　　　疾病

——————————————————

打喷嚏　护士　　　感冒

打喷嚏　农夫　　　过敏

头痛　　建筑工人　脑震荡

头痛　　建筑工人　感冒

打喷嚏　教师　　　感冒

头痛　　教师　　　脑震荡

现在又来了第七个病人，是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大？

根据贝叶斯定理：

P(A|B) = P(B|A) P(A) / P(B)

可得

P(感冒|打喷嚏x建筑工人)

= P(打喷嚏x建筑工人|感冒) x P(感冒) / P(打喷嚏x建筑工人)

假定”打喷嚏”和”建筑工人”这两个特征是独立的，因此，上面的等式就变成了

P(感冒|打喷嚏x建筑工人)= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒) / P(打喷嚏) x P(建筑工人)

这是可以计算的。

P(感冒|打喷嚏x建筑工人)= 0.66 x 0.33 x 0.5 / 0.5 x 0.33= 0.66

因此，这个打喷嚏的建筑工人，有66%的概率是得了感冒。同理，可以计算这个病人患上过敏或脑震荡的概率。比较这几个概率，就可以知道他最可能得什么病。

这就是贝叶斯分类器的基本方法：在统计资料的基础上，依据某些特征，计算各个类别的概率，从而实现分类。

 

(2)朴素贝叶斯分类器的公式

 

假设某个体有n项特征（Feature），分别为F1、F2、…、Fn。现有m个类别（Category），分别为C1、C2、…、Cm。贝叶斯分类器就是计算出概率最大的那个分类，也就是求下面这个算式的最大值：

P(C|F1F2...Fn) = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

由于 P(F1F2…Fn) 对于所有的类别都是相同的，可以省略，问题就变成了求

P(F1F2...Fn|C)P(C)的最大值。

朴素贝叶斯分类器则是更进一步，假设所有特征都彼此独立，因此

 P(F1F2...Fn|C)P(C) = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

上式等号右边的每一项，都可以从统计资料中得到，由此就可以计算出每个类别对应的概率，从而找出最大概率的那个类。

虽然”所有特征彼此独立”这个假设，在现实中不太可能成立，但是它可以大大简化计算，而且有研究表明对分类结果的准确性影响不大。

 

(3)拉普拉斯平滑（Laplace smoothing）

 也就是参数为1时的贝叶斯估计，当某个分量在总样本某个分类中（观察样本库/训练集）从没出现过，会导致整个实例的计算结果为0。为了解决这个问题，使用拉普拉斯平滑/加1平滑进行处理。

它的思想非常简单，就是对先验概率的分子（划分的计数）加1，分母加上类别数；对条件概率分子加1，分母加上对应特征的可能取值数量。这样在解决零概率问题的同时，也保证了概率和依然为1。

 eg：假设在文本分类中，有3个类，C1、C2、C3，在指定的训练样本中，某个词语F1，在各个类中观测计数分别为=0，990，10，即概率为P(F1/C1)=0，P(F1/C2)=0.99，P(F1/C3)=0.01，对这三个量使用拉普拉斯平滑的计算方法如下：

1/1003 = 0.001，991/1003=0.988，11/1003=0.011

3. 实际应用场景

 文本分类

垃圾邮件过滤

病人分类

拼写检查

--------------------- 

二, 条件概率

1.  条件概率公式

        设A,B是两个事件，且P(B)>0,则在事件B发生的条件下，事件A发生的条件概率（conditional probability)为：

                     P(A|B)=P(AB)/P(B)

         1.由条件概率公式得：

                       P(AB)=P(A|B)P(B)=P(B|A)P(A)    

             上式即为乘法公式；

         2.乘法公式的推广：对于任何正整数n≥2，当P(A₁A₂...A_n-1) > 0 时，有：

                 P(A₁A₂...A_n-1A_n)=P(A₁)P(A₂|A₁)P(A₃|A₁A₂)...P(A_n|A₁A₂...A_n-1)

2. 基本思想

• 条件概率（又称后验概率）：事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B)，读作“在B条件下A的概率”,。

  接着，考虑一个问题：P(A|B)是在B发生的情况下A发生的可能性。

• 首先，事件B发生之前，我们对事件A的发生有一个基本的概率判断，称为A的先验概率，用P(A)表示；
• 其次，事件B发生之后，我们对事件A的发生概率重新评估，称为A的后验概率，用P(A|B)表示；
• 类似的，事件A发生之前，我们对事件B的发生有一个基本的概率判断，称为B的先验概率，用P(B)表示；
• 同样，事件A发生之后，我们对事件B的发生概率重新评估，称为B的后验概率，用P(B|A)表示。

      贝叶斯定理便是基于下述贝叶斯公式：

P(A|B)=P(B|A)P(A)/P(B)

上述公式的推导其实非常简单，就是从条件概率推出。

 根据条件概率的定义，在事件B发生的条件下事件A发生的概率是

P(A|B)=P(A∩B)/P(B)

同样地，在事件A发生的条件下事件B发生的概率

P(B|A)=P(A∩B)/P(A)

整理与合并上述两个方程式，便可以得到：

P(A|B)P(B)=P(A∩B)=P(B|A)P(A)

    接着，上式两边同除以P(B)，若P(B)是非零的，我们便可以得到贝叶斯定理的公式表达式：

P(A|B)=P(B|A)*P(A)/P(B)

我们把P(A)称为"先验概率"（Prior probability），即在B事件发生之前，我们对A事件概率的一个判断。P(A|B)称为"后验概率"（Posterior probability），即在B事件发生之后，我们对A事件概率的重新评估。P(B|A)/P(B)称为"可能性函数"（Likelyhood），这是一个调整因子，使得预估概率更接近真实概率。

所以，条件概率可以理解成下面的式子：

后验概率　＝　先验概率 ｘ 调整因子

这就是贝叶斯推断的含义。我们先预估一个"先验概率"，然后加入实验结果，看这个实验到底是增强还是削弱了"先验概率"，由此得到更接近事实的"后验概率"。

在这里，如果"可能性函数"P(B|A)/P(B)>1，意味着"先验概率"被增强，事件A的发生的可能性变大；如果"可能性函数"=1，意味着B事件无助于判断事件A的可能性；如果"可能性函数"<1，意味着"先验概率"被削弱，事件A的可能性变小。

 贝叶斯定理应用示例:

已知某种疾病的发病率是0.001，即1000人中会有1个人得病。现有一种试剂可以检验患者是否得病，它的准确率是0.99，即在患者确实得病的情况下，它有99%的可能呈现阳性。它的误报率是5%，即在患者没有得病的情况下，它有5%的可能呈现阳性。现有一个病人的检验结果为阳性，请问他确实得病的可能性有多大？

假定A事件表示得病，那么P(A)为0.001。这就是"先验概率"，即没有做试验之前，我们预计的发病率。再假定B事件表示阳性，那么要计算的就是P(A|B)。这就是"后验概率"，即做了试验以后，对发病率的估计。

根据条件概率公式，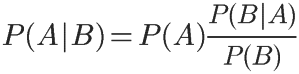

 

用全概率公式改写分母，

 

 

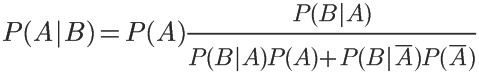
将数字代入，

 

我们得到了一个惊人的结果，P(A|B)约等于0.019。也就是说，即使检验呈现阳性，病人得病的概率，也只是从0.1%增加到了2%左右。这就是所谓的"假阳性"，即阳性结果完全不足以说明病人得病。

或许换成这个公式 P(A|B)=P(A∩B)/B，看起来更加直白写：

阐释：

如果没有误报，那么得病率：.001*.99

如果是误报，那么得病率为：.05*(1-.0001)，

所以：

p(A|B)=.001*.99/[.99*.001+.05*(1-.0001)]=.019

为什么会这样？为什么这种检验的准确率高达99%，但是可信度却不到2%？答案是与它的误报率太高有关。

三 全概率公式

 1. 如果事件组B₁，B₂，.... 满足

               1.B₁，B₂....两两互斥，即 B_i ∩ B_j = ∅ ，i≠j ， i,j=1，2，....，且P(B_i)>0,i=1,2,....;

               2.B₁∪B₂∪....=Ω ，则称事件组 B₁,B₂,...是样本空间Ω的一个划分

          设 B₁,B₂,...是样本空间Ω的一个划分，A为任一事件，则：

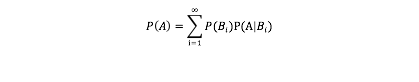
       上式即为全概率公式（formula of total probability)

       2.全概率公式的意义在于，当直接计算P(A)较为困难,而P(B_i),P(A|B_i)  (i=1,2,...)的计算较为简单时，可以利用全概率公式计算P(A)。思想就是，将事件A分解成几个小事件，通过求小事件的概率，然后相加从而求得事件A的概率，而将事件A进行分割的时候，不是直接对A进行分割，而是先找到样本空间Ω的一个个划分B₁,B₂,...B_n,这样事件A就被事件AB₁,AB₂,...AB_n分解成了n部分，即A=AB₁+AB₂+...+AB_n, 每一B_i发生都可能导致A发生相应的概率是P(A|B_i)，由加法公式得

         P(A)=P(AB₁)+P(AB₂)+....+P(AB_n)

               =P(A|B₁)P(B₁)+P(A|B₂)P(B₂)+...+P(A|B_n)P(PB_n)

        3.实例：某车间用甲、乙、丙三台机床进行生产，各台机床次品率分别为5%，4%，2%，它们各自的产品分别占总量的25%，35%，40%，将它们的产品混在一起，求任取一个产品是次品的概率。

                解：设.....     P(A)=25%*5%+4%*35%+2%*40%=0.0345

      4.简单举例

一个别人举的例子： 
一个村子与三个小偷，小偷偷村子的事件两两互斥，求村子被偷的概率。

解释：假设这三个小偷编号为A1,A2,A2； 
偷东西的事件标记为B,不偷的话标记为：B¯¯¯

那么被偷的概率就是：要么是A1，要么是A2，要么是A3， 
如果是A1, 概率是什么呢？首先得是A1,其次是村子被偷，也即是两个事件都满足，所以是P(A1B) 
同理，可以得到P(A2B),P(A3B)

又因这三个小偷两两互斥，表示不会同时去偷。所以被偷的概率是：

P(B)=P(A1B)+P(A2B)+P(A3B)

当然按照条件概率或者乘法公式展开： 
P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+P(A3)P(B|A3) （*）

PS: P(Ai),P(B|Ai)是已知的

问：是不是有想展开为：

P(B)=P(B)P(A1|B)+P(B)P(A1|B)+P(B)P(A1|B)的冲动？