欧拉函数的应用(hdu 3501)

原题链接 

http://acm.hdu.edu.cn/showproblem.php?pid=3501

Given a positive integer N, your task is to calculate the sum of the positive integers less than N which are not coprime to N. A is said to be coprime to B if A, B share no common positive divisors except 1.

 

Input
For each test case, there is a line containing a positive integer N(1 ≤ N ≤ 1000000000). A line containing a single 0 follows the last test case.
Output
For each test case, you should print the sum module 1000000007 in a line.
Sample Input
3
4
0
Sample Output
0
2
题意分析：

给一个整数n,求小于n且与n不互质的数的和

 

欧拉函数φ(n)的值为小于n且与n互质的数的个数（见文末），再想到gcd的一个性质如果gcd(n,i)=1,则gcd(n,n-i)=1,可以看出与n互质的数成对出现的，即欧拉函数的值为偶数(但φ(1)=1),且每一对的和都为n。

这样解题思路就出来了，用1-n的和减去n*φ(n)/2,即为答案

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <vector>
#include <math.h>
#include <map>
#include <queue>
#include <set>
using namespace std;
typedef long long ll;
const int maxn=1e5;
const int mod=1e9+7;
ll a[maxn];
//o(sqrt(n))求欧拉函数的值
int Phi(int n){
int m=(int)sqrt(n+0.5);
int ans=n;
for(int i=2;i<=m;i++){
if(n%i==0){
ans=ans/i*(i-1);
while(n%i==0) n/=i;
}
}
if(n>1) ans=ans/n*(n-1);
return ans;
}
int main()
{
ll n;
while(scanf("%lld",&n)!=-1&&n)
{
ll ans=(n*(n-1)/2)%mod;
ans-=(n*Phi(n)/2)%mod;
cout<<(ans+mod)%mod<<endl;
}
//printf("%lld\n",ans );
return 0;
}

 

欧拉函数φ：指从1到n-1与n互质的数的个数，特别的定义φ(1)=1下面给出其公式

 

 

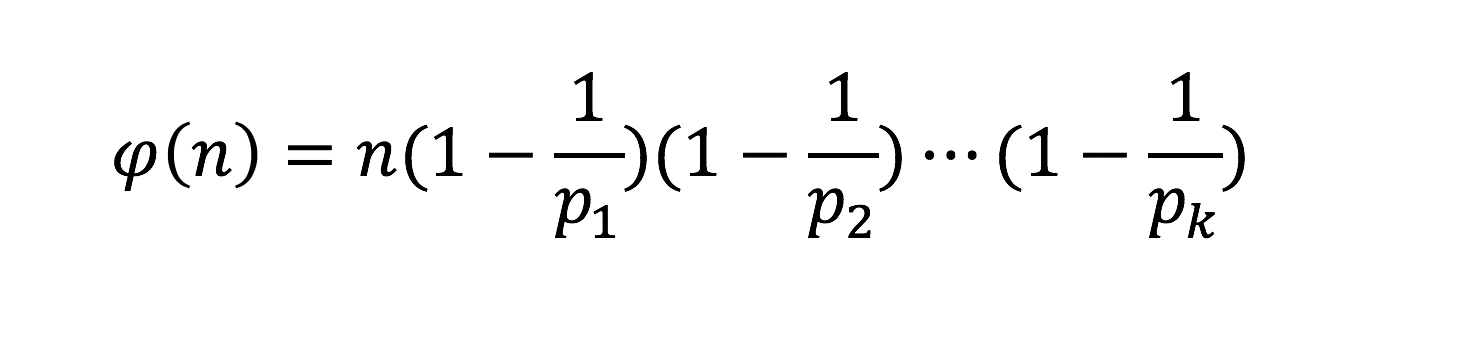
其中pi为n的素因子。