决策树模型

决策树

下面分成五个方面讲决策树。

1. 简介
2. 生成
3. 剪枝
4. 优缺点
5. sklearn 的使用建议

简介

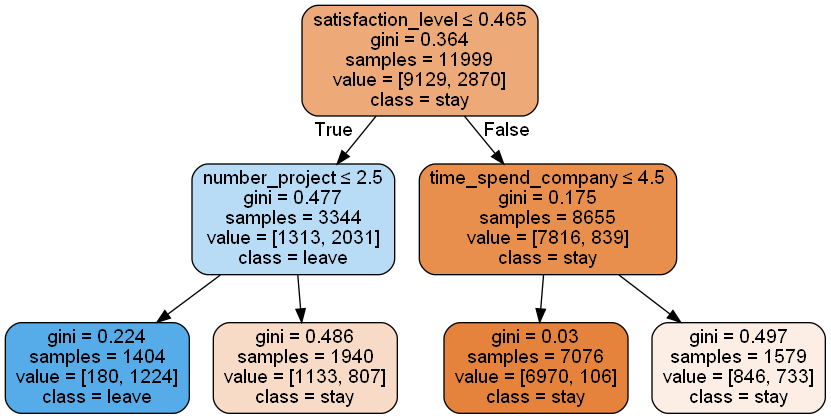
决策树，就是模拟人类决策的树。可以将决策树理解为一系列 if-else 的决策过程。下图数据来源于员工离职预测 [7]，使用 sklearn 生成 max_depth 为 2 的决策树。对于一组数据，根据结点上的属性，判断数据是否满足条件来选择走左分支还是右分支，不断走下去，直到叶子节点。

生成

决策树的生成主要参考周志华的机器学习，他在书里给出了一个基本的框架，不同的决策树生成算法区别在于决策树分裂的时候选择特征的标准。

代码中第 2 至 7 行表示终结条件。第 2 至 4 表示当输入的所有样本都来自于同一个类，那么没有必要继续分割了，生成这个类的节点。第 5 至 7 行表示输入样本的分割属性已经用完了，那么没有办法再分割了，选择样本最多的类别来生成节点。第 11 至 13 表示在分割的时候，取值为某个属性的样本根本就没有，那么这时选择他的父节点的样本分布来作为当前节点的先验分布。第 12 行写着 return，应该是 continue 才对吧，毕竟这个取值没有，那还要取别的取值嘛。第 13 至 15 行，递归调用生成节点。重点是代码第 8 行，如何选择最优划分属性，下一小节将会介绍三个划分属性选择的标准。

特征选择的标准

一、信息增益

ID3 用的就是信息增益。

首先定义熵，熵可以理解为一个事物的混乱程度，事物越乱，信息量越大。对于随机变量 \(X\)，我们可以定义熵值为：

\[H(X) = \sum_{i=1}^{n} p_i \log p_i \]

接着定义条件熵，将它定义为关于随机变量 \(X\) 的熵值的期望。

\[H(Y|X) = \sum_{i=1}^{n} p_i H(Y|X=i) \]

信息增益定义为上述两者的差值，他表示知道特征的信息后，数据集的信息量降低的程度。信息增益越大，知道特征信息后，信息量降低越多，说明这个特征能够提供的信息量越大。选择它来作为划分属性会更加合理。

\[g(D,A) = H(D) - H(D|A) \]

二、信息增益比

C4.5 用的就是信息增益比。提出 C4.5 是因为在样本量不够充足的情况下，信息增益偏向于选择特征取值较多的属性，具体的讨论可以看[5]。

信息增益比定义为信息增益和熵的比值。

\[g_{R}(D,A) = \frac{g(D,A)}{H(D)} \]

三、基尼指数

CART 用的就是基尼指数，由基尼提出来的，用来衡量年收入分配公平程度的指标。基尼系数越大，贫富差距就越大。将某个变量 \(X\) 的基尼指数定义为如下：

\[Gini(X) = \sum_{i=1}^{K} p_i (1-p_i) \]

假如 \(X\) 的取值为 \(0, 1\)，那么有

\[Gini(X) = 2p(1-p) \]

接下来给出关于特征 \(A\) 的基尼指数定义，假如数据集为 \(D\)，\(D_1\) 定义为 \(A(x)=a\) 的数据子集，\(D_2\) 定义为它的补集。

\[Gini(D,A) = \frac{|D_1|}{|D|} Gini(D_1) + \frac{|D_2|}{|D|} Gini(D_2) \]

我们可以这样来理解基尼系数：

基尼系数越大，贫富差距越大。在一个数据集中，我们可以将所谓的贫富差距理解为各个样本信息的不相同的程度。各个样本信息越不相同，那么整个数据集的信息量就越大。

在选择特征的时候，我们选择基尼系数 \(Gini(D,A)\) 小的特征。为什么呢？因为我们想要的是一个属性能够尽可能将数据集分成更加“纯粹”的两个部分，也就是将数据集分成基尼系数更小的部分。类比信息增益，我们可以搞一个所谓的“基尼增益”，将其定义为 \(Gini(D) - Gini(D,A)\)，\(Gini(D)\) 是保持不变的，所以选择 \(Gini(D,A)\) 更小的特征，我们就能得到更多的“基尼增益”。这意味着这个特征可以提供更多的信息。

剪枝

决策树的缺点在于太容易过拟合了，可以使用剪枝来减缓过拟合。一般有两种方法：一种是预剪枝，在生成树的过程中一边剪枝；另一种是后剪枝，在生成树之后进行剪枝。[1] 中的剪枝专门讲解了后剪枝的方法，使用了正则化的损失函数。正则化的意思是，将模型的复杂度引入到损失函数里面。[2] 介绍的剪枝方法使用验证集来决定是否剪枝。这里简单说说，后面就主要讲 [1] 的方法。

[2] 中介绍的剪枝方法，分为预剪枝和后剪枝。

1. 预剪枝，在生成树的过程中，使用验证集来计算当前节点的正确率，再计算产生分支节点之后的正确率。通过比较正确率来决定是否要划分节点。
2. 后剪枝，先完整地生成整个树，之后从最下面的分支节点往上进行处理。使用验证集来计算剪枝前后的准确率。

基于正则化的损失函数

将损失函数定义为，其中 \(T\) 表示树，\(|T|\) 表示树中的叶子节点个数：

\[C_{\alpha}(T) = C(T) + \alpha |T| \]

等号右边的式子，前者是预测误差，后者是模型的复杂度。

使用熵的损失函数

\[C_{\alpha}(T) = C(T) + \alpha |T| \]

\(H_t(T)\) 定义为某个叶子节点 \(t\) 的熵：

\[C(T) = \sum_{t=1}^{|T|} N_t H_t(T) = - \sum_{t=1}^{|T|} \sum_{k=1}^{K} N_{tk} \log{\frac{N_{tk}}{N_t}} \]

之后的剪枝计算类似 [2] 中描述的那样，从下往上计算每个点的损失函数，如果损失函数在剪掉之后降低了，那么就进行一次剪枝。

CART 的损失函数

上面描述的过程，\(\alpha\) 是手动设定的。那么有没有一种方法可以不用手动设定呢？[1] 中介绍的 CART 的剪枝方法就可以找到那个合适的 \(\alpha\) 并且能够找到对应的决策树。

对树中的某个节点 \(t\)，我们可以定义以 \(t\) 为单节点树的损失函数为：

\[C_{\alpha}(t) = C(t) + \alpha \]

我们还可以定义以 \(t\) 为根节点的树的损失函数为：

\[C_{\alpha}(T_t) = C(T_t) + \alpha |T_t| \]

当这两个损失函数相等的时候，对其剪枝可以减低模型复杂度。

\[C_{\alpha}(t) = C_{\alpha}(T_t) \]

\[\alpha = \frac{C(t) - C(T_t)}{|T_t| - 1} \]

\[g(t) = \alpha \]

这里还要论证一点，为什么 \(\alpha\) 要从小到大进行？[8]

(5.29)认为，在 \(\alpha\) 为 \(0\) 或者足够小的情况下，有不等式 \(C_{\alpha}(T_t) < C_{\alpha}(t)\)，在 \(\alpha\) 增大的过程中，会使到\(C_{\alpha}(T_t) = C_{\alpha}(t)\)，再大，不等式就翻转了方向。对于不同的节点，每个节点都有一个 \(\alpha_k\)，这个 \(\alpha_k\) 表示在 \(\alpha \ge \alpha_k\) 的情况下，有 \(C_{\alpha}(T_t) > C_{\alpha}(t)\)，损失函数减小了，可以进行剪枝。于是，我们就从小到大增加 \(\alpha\)，逐个剪去节点。

[1] 中的算法描述如下，对于 (6)，回到 (4) 的时候，还需要正确设置 \(\alpha\)，应该按照升序选择一个 \(\alpha\)。

决策树优缺点

下面翻译自 Wikipedia。

优点：

1. 容易理解，结果可以解释。
2. 能处理数值型和类别型数据，其他模型只能处理其中一种。
3. 减少数据预处理。不用归一化，标准化，one-hot。
4. 非统计学的方法，对训练数据不用做出假设。
5. 能够处理大数据集。
6. 更像人类做决策的样子。
7. 特征选择。决策树中越接近根节点的分裂特征，更加重要。

缺点：

1. 不够健壮，训练数据中小小的改变可能导致决策树的变化，从而改变了预测结果。
2. 学习到最优的决策树是一个 NP-complete 问题，决策树的学习算法是一种启发式的算法，比如贪心选择局部最优的分裂属性。这可能导致找不到最好的决策树。
3. 决策树容易过拟合。可以使用剪枝来避免这个问题。
4. 使用信息增益来选取特征时，存在偏向于选择取值较多的特征。[1] 也提到了这个问题，建议使用信息增益比可以校正这个问题。[5] 对这个问题进行了讨论，这里说说我看到之后的理解：当不同特征的不同类别的数量足够多的时候，不会有这种偏向性。当某些特征的样本较少的时候，才有可能出现这种偏向性。出现的原因来自于熵的计算过程中，我们使用样本出现的频率去接近概率，而这只有在样本足够多的情况下是满足的。

sklearn 使用建议

• 决策树容易在大量特征的数据集上面过拟合，平衡好特征数量和数据集大小很重要，因为决策树很容易在大量特征的小数据集上过拟合。
• 在学习之前，考虑降维(PCA, ICA, 特征选择)。
• 使用 export 函数可视化决策树，可以从最大高度为 3 开始，然后逐渐加大最大高度。
• 决策树每增长一层，需要的样本数量就翻一倍。使用 max_depth 来避免过拟合
• 使用 min_samples_split 或 min_samples_leaf 来控制决策树的分裂，小的数值容易过拟合，大的数值使决策树学习效果差。如果样本大小变化较大，可以使用百分比。对于只有少数几个类别的分类问题，min_samples_leaf=1 效果往往不错。
• 平衡你的数据集，不然决策树会倾向于占主导地位的类。样本平衡可以通过给每个不同类别采样相同的样本数量来实现。最好是将每个类的样本权重之和(sample_weight)归一化到相同值，具体操作请看[6]。预剪枝中，使用 min_weight_fraction_leaf 不偏向于多数类。
• 如果样本是加权的，预剪枝使用 min_weight_fraction_leaf 会更好
• 决策树内部使用 np.float32，如果训练数据不是这个格式，那么将会复制一份数据。
• 如果输入的矩阵 X 很稀疏，建议在 fit 和 predict 之前将数据转为 csc_matrix 和 csr_matrix。训练速度将会大大提高。

参考资料

[1] 李航统计学习方法
[2] 周志华机器学习
[3] https://en.wikipedia.org/wiki/Decision_tree_learning
[4] https://scikit-learn.org/stable/modules/tree.html
[5] https://www.zhihu.com/question/22928442
[6] https://stackoverflow.com/questions/34389624/what-does-sample-weight-do-to-the-way-a-decisiontreeclassifier-works-in-skle
[7] https://god.yanxishe.com/93
[8] https://www.zhihu.com/question/22697086