移动最小二乘法在点云平滑和重采样中的应用
导言
这篇博客的目的是介绍移动最小二乘法(moving least squares)在点云平滑和重采样的应用。开头先简要介绍最小二乘法,用两种不同的方法来求解最小二乘法,并给出一个具体的算例、代码、数据。目前关于最小二乘法的博客和网上的讨论有很多,我没必要重复做这个工作(其实是我太菜不能形象的讲出来哈),我想做的是提供一个简要的概括,以及给出一个具体的例子帮助读者理解。接下来,介绍加权最小二乘法,在同样的数据上面,跑加权最小二乘法,看看拟合的结果又如何。之后,简略分析一下PCL是如何实现的点云平滑和重采样。参考的文献列在最后,比较有价值的是[1][2],基本上是看这两个理解的移动最小二乘法。由于我学力尚浅,自知这篇文章有很多的不足、错误,希望读者不吝指出。欢迎理性的讨论和交流。
最小二乘法
对于方程组\(A\mathbf{x}=b\),我们要去寻找一个\(Ax'\)最佳逼近b,即有
解释一下为什么是这样。对于方程组\(A\mathbf{x}=b\),我们并不一定可以在\(A\)的各列的线性组合找到\(b\),换句话说,找不到这样的 \(x\) 使等式成立,因此我们尝试在 \(A\) 的列空间中找到最逼近b的那个点。
使用投影的方法来求解
将向量\(b\)投影到\(A\)的列空间得到\(b'\),\((b - b')\)是正交于A的列空间,即有
如果\((A^T*A)\)可逆:
例1
这组数据,来自于[2]。画出散点图。
x = [0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
y = [0, 4, 5, 14, 15, 14.5, 14, 12, 10, 5, 4]
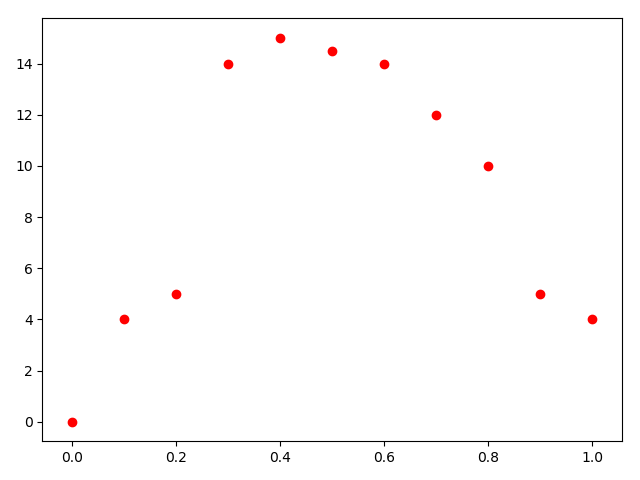
首先考虑使用\(y = mx + n\)来拟合(这里用m,n而不用a,b是怕读者混淆)。需要解决的问题是数据如何装填。A矩阵放什么,b放什么,x又是什么。
欲求的是\(m,n\)。\(x = [m \quad n]^T\),\(b\)放入的是每一个因变量。欲求\(Ax = b\),那么每一行A乘以x,会等于对应的每一行b:
A = np.empty((0, 2))
B = np.empty((0, 1))
for (a, b) in zip(x, y):
row1 = np.array([a, 1])
row2 = np.array([b])
A = np.vstack([A, row1])
B = np.vstack([B, row2])
ans = np.linalg.inv(np.mat(A.transpose()) * np.mat(A)) * np.mat(A.transpose()) * np.mat(B)
print(ans)
xx = np.arange(0, 1, 0.01)
yy = ans[0, 0] * xx + ans[1, 0]
plt.plot(xx, yy)
plt.scatter(x, y, c='r')
plt.show()
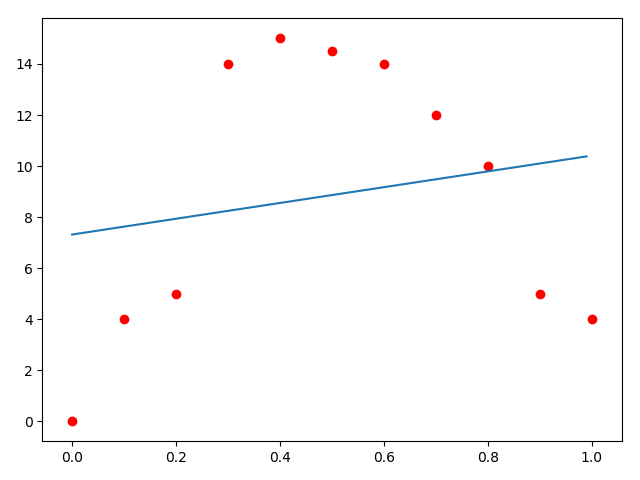
拟合结果:
例2
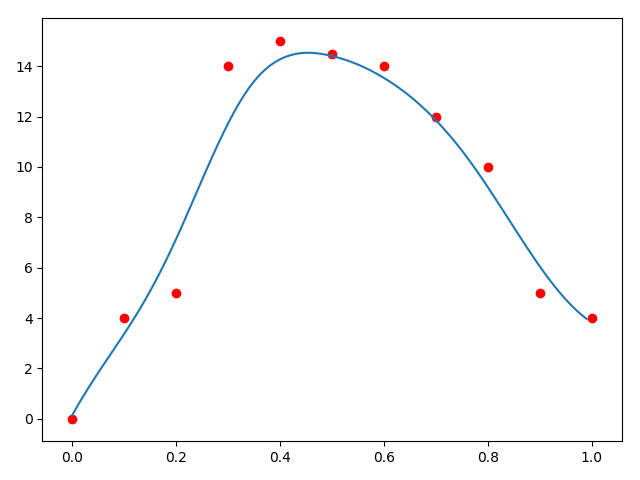
可是这个拟合的结果太差劲了吧!我们观察数据,觉得这个可以用二次函数去拟合,那么可以使用新的拟合函数:\(y = ax^2 + bx + c\)
再拟合一次:这次拟合的还行。\(a = -53.96270396, b = 57.05361305, c = -0.77622378\)
A = np.empty((0, 3))
B = np.empty((0, 1))
for (a, b) in zip(x, y):
row1 = np.array([a*a, a, 1])
row2 = np.array([b])
A = np.vstack([A, row1])
B = np.vstack([B, row2])
print(A)
print(B)
ans = np.linalg.inv(np.mat(A.transpose()) * np.mat(A)) * np.mat(A.transpose()) * np.mat(B)
print(ans)
xx = np.arange(0, 1, 0.01)
yy = ans[0, 0] * xx**2 + ans[1, 0] * xx + ans[2, 0]
plt.plot(xx, yy)
plt.scatter(x, y, c='r')
plt.show()
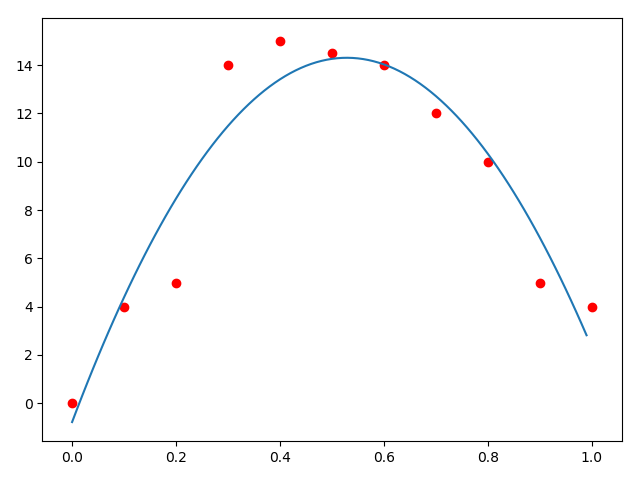
使用求偏导的方法来求解
另一种理解最小二乘法的方法是,找到使因变量的误差平方和最小的参数来求解。假设我们有二维数据点集\((x_i, y_i)\),对他拟合的函数为\(f(x)\)。
于是问题化解为求\(min(J_{LS})\)。
为什么使用误差平方和呢?我觉得沟通这个方法和上一个方法的关键在于距离!误差平方和,其实是因变量的向量\((y_1, y_2, ... , y_n)\)和拟合函数对应函数值的向量\((f(x_1), f(x_2), ... , f(x_n))\)的距离平方。要使到这个距离最小,那就是投影!其实这两种方法本质上都是利用投影来使到偏差最小。不同之处在于一种使用了内积为0的方式来求,一种使用求偏导算最小值的方式来求。
[1][2]都是用了一个系数向量\(\alpha\),和基函数\(p(x)\)来表示\(f(x) = p(x)^T * \alpha\)。
如果有一个自变量x,最高阶为3,那么\(p(x) = [1,x,x^2,x^3]^T\)
如果有两个自变量x、y,最高阶为2,那么\(p(x) = [1, x, y, x^2, xy, y^2]^T\)
系数向量是我们想要求的向量, \(\alpha = [c_1, c_2, ..., c_n]\)。
对\(J_{LS}\)分别求\(c_1, c_2, ..., c_n\)的偏导,具体过程参考[1]
令偏导为0
注意到\(p(x_i)\)是一个\(n\times 1\)的向量,他的转置则是\(1\times n\),于是它和它的转置相乘是一个\(n\times n\)的矩阵。
例子3
使用例子2的函数去拟合:\(y = a + bx + cx^2\)
基函数\(p(x) = [1, x, x^2]^T\), 系数向量\(\alpha = [a, b, c]\)
拟合出来的结果为:\(a=-0.77622378,b=57.05361305,c=-53.96270396\)。殊途同归啊!
sumx = sumxx = sumxxx = sumxxxx = sumf = sumxf = sumxxf = 0
for (a, b) in zip(x, y):
sumx += a
sumxx += a ** 2
sumxxx += a ** 3
sumxxxx += a ** 4
sumf += b
sumxf += a * b
sumxxf += a * a * b
A = np.array([[len(x), sumx, sumxx],
[sumx, sumxx, sumxxx],
[sumxx, sumxxx, sumxxxx]])
B = np.array([sumf, sumxf, sumxxf])
ans = np.linalg.solve(A, B)
print(ans)
xx = np.arange(0, 1, 0.01)
yy = ans[0] + ans[1] * xx + ans[2] * xx**2
plt.plot(xx, yy)
plt.scatter(x, y, c='r')
plt.show()
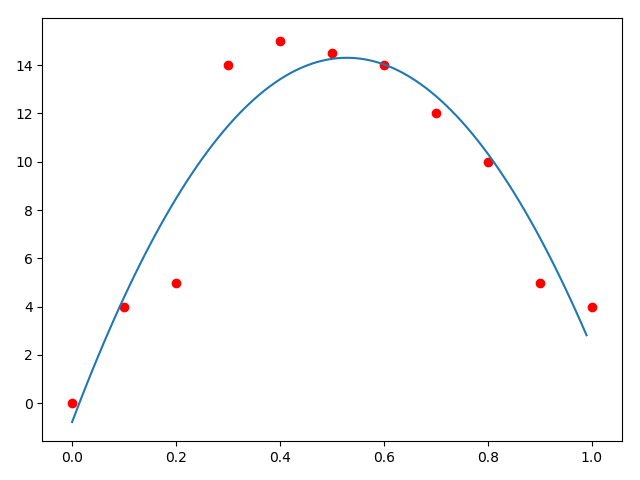
加权最小二乘法
[2]论文中:
引入紧支( Compact Support)概念,认为点 x 处的值 y 只受 x 附近子域内节点影响
因变量只受到自变量某一邻域影响,引入一个权重函数,给重要的地方加权,不重要的地方削弱它对因变量的影响。
其中\(s\)为想要求的自变量\(x\)到附近样本自变量的欧几里得距离。
如果我们想根据一组数据去估计某一个自变量\(x\)的函数值,我们就得计算一次!这种方法计算量相对而言大很多。
同样这是一个最小化问题\(min(J_{WLS})\),对它求偏导,令偏导为0。
例子4
仍然是那一组数据。使用[2]建议的加权函数来求解。只不过这次使用的是一个一次函数来拟合局部。\(p(x) = [1,x]^T\)
所谓的移动最小二乘法,找到一个函数,这个函数有一系列的局部的函数组成\(f(x) \in f_X(x)\),本质上就是WLS。
def w(dis):
dis = dis / 0.3
if dis < 0:
return 0
elif dis <= 0.5:
return 2/3 - 4 * dis**2 + 4 * dis**3
elif dis <= 1:
return 4/3 - 4 * dis + 4 * dis**2 - 4/3 * dis**3
else:
return 0
def mls(x_):
sumxx = sumx = sumxf = sumf = sumw = 0
for (a, b) in zip(x, y):
weight = w(abs(x_ - a))
sumw += weight
sumx += a * weight
sumxx += a * a * weight
sumf += b * weight
sumxf += a * b * weight
A = np.array([[sumw, sumx],
[sumx, sumxx]])
B = np.array([sumf, sumxf])
ans = np.linalg.solve(A, B)
return ans[0] + ans[1] * x_
x = [0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
y = [0, 4, 5, 14, 15, 14.5, 14, 12, 10, 5, 4]
xx = np.arange(0, 1, 0.01)
yy = [mls(xi) for xi in xx]
plt.plot(xx, yy)
plt.scatter(x, y, c='r')
plt.show()
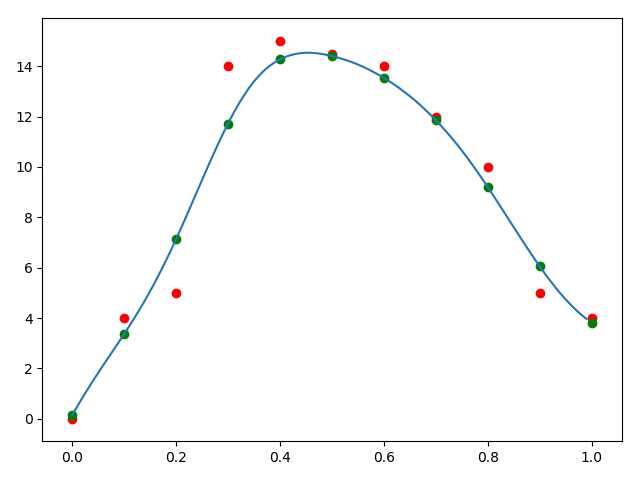
使用mls平滑
简单来说就是对每个样本计算一次加权最小二乘法,然后对该样本的自变量\(x_i\)求函数值\(f_X(x_i)\),算出来的\((x, f_X(x_i))\)就是平滑的结果。
PCL中upsampling的实现
RANDOM_UNIFORM_DENSITY
在点的某个范围内,如果有足够的点,就不进行重采样。如果不够,那么就随机添加点到这个范围内,投影到计算出来的曲面上,直到达到足够的点数。
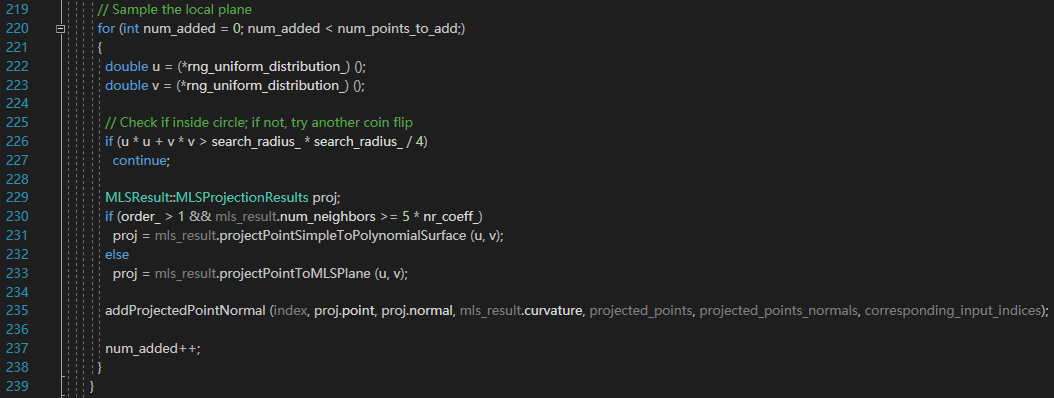
SAMPLE_LOCAL_PLANE
这个方法更加直接,按照一定的步长,一个一个点,整齐的添加点。

Voronoi图上upsampling
[3]中,使用一种在Voronoi图上重采样的方法。
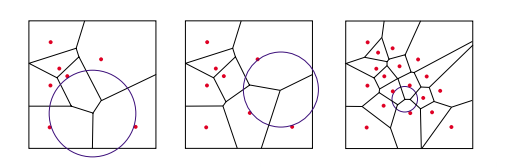
思路:从输入的点云里面选点,在局部做一个平面的拟合,将这些点投影到平面上。计算这些点的Voronoi图,每次选择Voronoi节点中到它临近点(多于三个点)最大的那个节点,作为一个新的点,将它投影到拟合出来的mls曲面上。重复这个过程,直到Voronoi到它的临近点的半径小于某个阈值为止。
结语
完。第一篇博客,欢迎理性的讨论。不足、错误之处,希望读者不吝指出。
参考
[1] http://www.nealen.com/projects/mls/asapmls.pdf
[2] https://wenku.baidu.com/view/fe7a74976f1aff00bed51eb1.html
[3] http://www.sci.utah.edu/~shachar/Publications/crpss.pdf

