数据挖掘模型
数据挖掘模型
挖掘建模根据挖掘目标和数据形式可建立：分类与预测、聚类分析、关联规则、时序模式、偏差检测等模型
1.分类与预测
分类与预测是预测问题的两种主要类型，分类主要是：预测分类标号（离散属性）；预测主要是：建立连续值函数模型，预测给定自变量对应的因变量的值。
1.1 实现过程
（1）分类
分类是构造一个分类模型，输入样本属性值，输出对应类别，将每个样本映射到预先定义好的类别。
分类模型，建立在已有类标记的数据集上，因此，属于“有监督学习”
（2）预测
预测，指建立两种或两种以上变量间相互依赖的函数模型，进行预测或控制
（3）实现过程
分类算法：
a:学习步，通过归纳分析训练样本集建立分类模型得到分类规则；
b:分类步，先用已知的测试样本集，评估分类规则的准确率
预测模型：
a:通过训练集建立预测属性的函数模型
b:在模型通过检验后进行预测或控制
1.2 常用分类与预测算法
| 算法名称 | 算法描述 |
| 回归分析 | 回归分析，确定预测属性与其他变量间相互依赖的定量关系。包括：线性回归、非线性回归、Logistic回归、岭回归、主成分回归、偏最小二乘回归等模型 |
| 决策树 | 决策树采用自顶向下的递归方式，在内部节点进行属性值比较，并根据不同的属性值从该节点向下分支，最终得到的叶节点是学习划分的类 |
| 人工神经网络 | 人工神经网络是一种模仿大脑神经网络结构和功能而建立的信息处理系统，表示神经网络的输入与输出变量之间关系的模型 |
| 贝叶斯网络 | 贝叶斯网络又称信度网络，是Bayes方法的扩展，是目前不确定知识表达和推理领域最有效的理论模型之一 |
| 支持向量机 | 支持向量机是一种通过某种非线性映射，把低维的非线性可分转化为高维的线性可分，在高维空间进行线性分析的算法 |
1.3 回归分析
| 回归模型名称 | 适用条件 | 算法描述 |
| 线性回归 | 因变量与自变量是线性关系 | 对一个或多个自变量和因变量间的线性关系进行建模，可用最小二乘法求解模型系数 |
| 非线性回归 | 因变量与自变量间不都是线性关系 | 对一个或多个自变量和因变量间的非线性关系进行建模。若非线性关系可通过简单的函数变换转化成线性关系，用线性回归的思想求解，若不能转化，用非线性最小二乘法求解 |
| Logistic回归 | 因变量一般有1和0（是、否）两种取值 | 广义线性回归模型的特例，利用Logistic函数将因变量的取值范围控制在0、1之间，表示取值为1的概率 |
| 岭回归 | 参与建模的自变量间具有多重共线性 | 是一种改进最小二乘估计的方法 |
| 主成分回归 | 参与建模的自变量间具有多重共线性 | 主成分回归是根据主成分分析的思想提出的，是对最小二乘法的改进，它是参数估计的一种有偏估计。可消除自变量间的多重共线性 |
Logistic回归建模步骤：
（1）根据分析目的设置指标变量（因变量和自变量），收集数据，根据收集到的数据，对特征(y,x1,x2....xp)进行筛选
（2）y=1时，概率p=P(y=1|X)；y=0,概率为1-p。用In(p/(1-p))和自变量列出线性回归方程：In(p/(1-p))=β0+β1x1+.....+βpxp+ε
（3）估计回归系数
（4）进行模型检验
（5）模型应用：输入自变量的取值，得到预测变量的值或根据得到预测变量的值取控制自变量的取值
利用Scikit-Learn逻辑回归分析步骤：
首先，进行特征筛选，
特征筛选方法：
a:通过F检验给出各个特征的F值和p值，筛选变量（选择F值大或p值小的特征）；
b:递归特征消除：主要思想是反复构建模型，选出最好的（最差的）特征（可根据系数来选），将选出的特征放在一边，在剩余的特征里重复这个过程，直至遍历所有特征。
该过程中特征被消除的次序即是：特征的排序。因此，也是一种寻找最优特征子集的贪心算法。
c:稳定性：一种基于二次抽样和选择算法相结合较新的方法，主要思想是：在不同的数据子集和特征的子集上运行特征选择算法，不断重复，最终汇总特征选择结果。
然后，利用筛选后的特征建立逻辑回归模型，输出平均正确率
#-*- coding: utf-8 -*-
#逻辑回归 自动建模
import pandas as pd
#参数初始化
filename = '../data/bankloan.xls'
data = pd.read_excel(filename)
x = data.iloc[:,:8].as_matrix()
y = data.iloc[:,8].as_matrix()
from sklearn.linear_model import LogisticRegression as LR
from sklearn.linear_model import RandomizedLogisticRegression as RLR
rlr = RLR() #建立随机逻辑回归模型，筛选变量
rlr.fit(x, y) #训练模型
rlr.get_support() #获取特征筛选结果，也可以通过.scores_方法获取各个特征的分数
print(u'通过随机逻辑回归模型筛选特征结束。')
print(u'有效特征为：%s' % ','.join(data.columns[rlr.get_support()]))
x = data[data.columns[rlr.get_support()]].as_matrix() #筛选好特征
lr = LR() #建立逻辑货柜模型
lr.fit(x, y) #用筛选后的特征数据来训练模型
print(u'逻辑回归模型训练结束。')
print(u'模型的平均正确率为：%s' % lr.score(x, y)) #给出模型的平均正确率，本例为81.4%
1.4 决策树
决策树是一种树状结构，它的每一个叶节点对应着一个分类，非叶节点对应着在某个属性上的划分，根据样本在该属性不同取值将其划分为若干个子集。
决策树构造的核心问题：在每一步如何选择适当的属性对样本做拆分。
决策树处理过程：对分类问题，应从已知类标记的训练样本中学习并构造出决策树，自上而下，分开进行解决。
| 决策树算法 | 算法描述 |
| ID3算法 | 核心：在决策树的各级节点上，使用信息增益方法作为属性的选择标准，来帮助确定生成每个节点时所应采用的合适属性。 |
| C4.5算法 | C4.5决策树生成算法相对于ID3算法的重要改进：使用信息增益率来选择节点属性。C4.5可客服ID3算法的不足：ID3算法只适用于离散的描述属性，而C4.5算法既能处理离散的描述属性，也可处理连续的描述属性 |
| CART算法 | CART决策树是一种非参数分类和回归方法，通过构建树、修剪树、评估树来构造一个二叉树。当终结点是连续变量时，该树为回归树；当终结点是分类变量，该树为分类树 |
ID3算法原理：
ID3算法流程：
（1）对当前样本集合，计算所有属性的信息增益；
（2）选择信息增益最大的属性作为测试属性，把测试属性取值相同的样本划分为同一个子样本集；
（3）若子样本集的类别属性只含有单个属性，则分支为叶子节点，判断其属性值并标上相应的符号，然后返回调用处；否则对子样本集递归调用本算法。
#-*- coding: utf-8 -*-
#使用ID3决策树算法预测销量高低
import pandas as pd
#参数初始化
inputfile = '../data/sales_data.xls'
data = pd.read_excel(inputfile, index_col = u'序号') #导入数据
#数据是类别标签，要将它转换为数据
#用1来表示“好”、“是”、“高”这三个属性，用-1来表示“坏”、“否”、“低”
data[data == u'好'] = 1
data[data == u'是'] = 1
data[data == u'高'] = 1
data[data != 1] = -1
x = data.iloc[:,:3].as_matrix().astype(int)
y = data.iloc[:,3].as_matrix().astype(int)
from sklearn.tree import DecisionTreeClassifier as DTC
dtc = DTC(criterion='entropy') #建立决策树模型，基于信息熵
dtc.fit(x, y) #训练模型
#导入相关函数，可视化决策树。
#导出的结果是一个dot文件，需要安装Graphviz才能将它转换为pdf或png等格式。
from sklearn.tree import export_graphviz
x = pd.DataFrame(x)
from sklearn.externals.six import StringIO
x = pd.DataFrame(x)
with open("tree.dot", 'w') as f:
f = export_graphviz(dtc, feature_names = x.columns, out_file = f)
1.5 人工神经网络
人工神经网络：模拟生物神经网络进行信息处理的一种数学模型。
人工神经网络的学习也称为训练，指的是：神经网络在受到外部环境的刺激下调整神经网络的参数，使神经网络以一种新的方式对外部环境做出反应的一个过程。
分类预测时，人工神经网络主要使用有指导的学习方式，即根据给定的训练样本调整人工神经网络参数使网络输出接近于已知的样本类标记或其他形式的因变量。
分类预测时，常用的算法是：误差校正学习算法
误差校正算法，根据神经网络的输出误差对神经元的连接强度进行修正，属于有指导学习。
设神经网络中神经元i作为输入，神经元j为输出神经元，它们的连接权值为wij，则对权值的修正为△wij=ηδjYi，其中η为学习率，δj=Tj-Yj为j的偏差，即输出神经元j的实际输出和教师信号之差。
神经网络训练是否完成通过误差函数E衡量。当误差函数小于某个设定值时，停止神经网络训练。
误差函数计算：
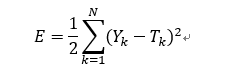，N为训练样本个数。
人工神经网络算法
| 算法名称 | 算法描述 |
| BP神经网络 | 一种按误差逆传播算法训练的多层前馈网络，学习算法是：误差校正学习算法 |
| LM神经网络 | 基于梯度下降法和牛顿法结合的多层前馈网络，特点 ：迭代次数少，收敛速度快，精确度高 |
| RBF径向基神经网络 | RBF网络能以任何精度逼近任意连续函数，从输入层到隐含层的变换是非线性的，而从隐含层到输出层的变换是线性的，适用于解决分类问题 |
| FNN模糊神经网络 | FNN是具有模糊权系数或输入信号是模糊量的神经网络 |
| GMDH神经网络 | GMDH是前馈神经网络中常用的一种用于预测的神经网络。它的特点：网络结构不固定，在训练中不断改变 |
| ANFIS自适应神经网络 | 神经网络嵌在一个全部模糊的结构中，不知不觉中向训练数据学习，自动产生、修正并高度概括出最佳的输入与输出变量的隶属函数及模糊规则 |
BP算法
BP算法的学习过程由：信号的正向传播及误差的逆向传播组成。
正向传播时，输入信号经过隐层的处理，传向输出层。
若输出层节点未能得到期望的输出，则转入误差的逆向传播。
逆向传播时，将输出误差按某种子形式，通过隐层向输出层返回，并分摊给隐层的节点与输入层节点，获得各层单元的参考误差，作为修改各单元权值的依据。
信号正向及逆向传播周而复始，不断修改权值，即神经网络的训练过程。
算法开始时，给定学习次数上限，初始化学习次数为0，对权值和阙值赋予小的随机数，一般在[-1,1]。
输入样本数据，网络正向传播，得到中间层与输出层的值，比较输出层的值与教师信号的误差，用误差函数判断误差是否小于误差上限。
若不小于误差上限，则对中间层和输出层权值和阙值进行更新
更新权值和阙值后，再次将样本数据作为输入，重复计算误差E。
算法结束两条依据：达到学习次数货误差达到预期
#-*- coding: utf-8 -*-
#使用神经网络算法预测销量高低
import pandas as pd
#参数初始化
inputfile = '../data/sales_data.xls'
data = pd.read_excel(inputfile, index_col = u'序号') #导入数据
#数据是类别标签，要将它转换为数据
#用1来表示“好”、“是”、“高”这三个属性，用0来表示“坏”、“否”、“低”
data[data == u'好'] = 1
data[data == u'是'] = 1
data[data == u'高'] = 1
data[data != 1] = 0
x = data.iloc[:,:3].as_matrix().astype(int)
y = data.iloc[:,3].as_matrix().astype(int)
from keras.models import Sequential
from keras.layers.core import Dense, Activation
model = Sequential() #建立模型
model.add(Dense(input_dim = 3, output_dim = 10))
model.add(Activation('relu')) #用relu函数作为激活函数，能够大幅提供准确度
model.add(Dense(input_dim = 10, output_dim = 1))
model.add(Activation('sigmoid')) #由于是0-1输出，用sigmoid函数作为激活函数
model.compile(loss = 'binary_crossentropy', optimizer = 'adam', class_mode = 'binary')
#编译模型。由于我们做的是二元分类，所以我们指定损失函数为binary_crossentropy，以及模式为binary
#另外常见的损失函数还有mean_squared_error、categorical_crossentropy等，请阅读帮助文件。
#求解方法我们指定用adam，还有sgd、rmsprop等可选
model.fit(x, y, nb_epoch = 1000, batch_size = 10) #训练模型，学习一千次
yp = model.predict_classes(x).reshape(len(y)) #分类预测
from cm_plot import * #导入自行编写的混淆矩阵可视化函数
cm_plot(y,yp).show() #显示混淆矩阵可视化结果
1.6 分类与预测算法评价
分类与预测模型对训练集进行预测，得到的准确率，不能很好的反映预测模型未来的性能
为有效判断一个预测模型的性能表现，需一组没有参与预测模型建立的数据集，并在该数据集上评价预测模型的准确率，这组独立的数据集叫测试集。
模型预测效果评价指标：
（1）绝对误差E与相对误差e
（2）平均绝对误差MAE
（3）均方误差MSE
（4）均方根误差RMSE
（5）平均绝对百分误差MAPE（一般认为MAPE小于10时，预测精度较高）
（6）Kappa统计
Kappa统计是比较两个或多个观测者对同一事物，或观测者对同一事物的两次或多次观测结果是否一致。Kappa统计量和加权Kappa统计量不仅可以用于无序和有序分类变量资料的一致性，重现性检验。
Kappa取值在[-1，+1]间时：
Kappa=+1，说明两次判断结果完全一致；
Kappa=-1，说明两次判断结果完全不一致
Kappa<0，说明一致程度比机遇造成的还差，两次结果很不一致，在实际应用中毫无意义
Kappa>0，说明有意义，Kappa越大，说明一致性越好
Kappa≥0.75，说明已经取得相当满意的一致程度
Kappa<0，说明一致程度不够
（7）识别准确度Accuracy
Accuracy=(TP+FN)/(TP+TN+FP+FN)
TP为正确的肯定表示正确肯定的分类数，TN为正确的否定表示正确否定的分类数；
FP为错误的肯定表示错误肯定的分类数，FN为错误的否定表示错误否定的分类数。
（8）识别精确率Precision
Precision=TP/(TP+FP)
（9）反馈率Recall
Recall=TP/(TP+TN)
（10）ROC曲线
（11）混淆矩阵
1.7 Python分类与预测模型特点
| 模型 | 模型特点 | 位置 |
| 逻辑回归 | 较基础的线性分类模型 | sklearn.linear_model |
| SVM | 可用来回归、预测、分类等，根据选取不同的核函数。模型可以是线性的/非线性的 | sklearn.svm |
| 决策树 | 基于“分类讨论、逐步细化”思想的分类模型，模型直观 | sklearn.tree |
| 随机森林 | 思想跟决策树类似，精度通常比决策树要高，缺点是由于其随机性，丧失了决策树的可解释性 | sklearn.ensemble |
| 朴素贝叶斯 | 基于概率思想的简单有效的分类模型，能给出容易理解的概率解释 | sklearn.naive_bayes |
| 神经网络 | 具有强大的拟合能力，可用于拟合、分类等，它有很多个增强版本 | Keras |
2.聚类分析
2.1 常用聚类分析算法
聚类分析是在没有给定划分类别的情况下，根据数据相似度进行样本分组的一种方法。
聚类模型建立在无类标记的数据上，是一种非监督的学习算法。
聚类的输入是一组未被标记的样本，聚类根据数据自身的距离或相似度将其划分为若干组，划分原则是：组内距离最小化而组间距离最大化。
常用聚类方法：
| 类别 | 包括的主要算法 |
| 划分（分裂）方法 | K-Means算法（K-平均）、K-MEDOIDS算法（K-中心点）、CLARANS算法（基于选择的算法） |
| 层次分析方法 | BIRCH算法（平衡迭代规约和聚类）、CURE算法（代表点聚类）、CHAMELEON算法（动态模型） |
| 基于密度的方法 | DBSCAN算法（基于高密度连接区域）、DENCLUE算法（密度分布函数）、OPTICS算法（对象排序识别） |
| 基于网格的方法 | STING算法（统计信息网络）、CLIOUE算法（聚类高维空间）、WAVE-CLUSTER算法（小波变换） |
| 基于模型的方法 | 统计学方法、神经网络方法 |
常用聚类算法：
| 算法名称 | 算法描述 |
| K-Means | K-均值聚类（快速聚类发），在最小化误差函数的基础上将数据划分为预定的类数K。该算法原理简单便于处理大量数据。 |
| K-中心点 | K-均值算法对孤立点的敏感性，K-中心点算法不采用簇中对象的平均值作为簇中心，选用簇中离平均值最近的对象作为簇中心。 |
| 系统聚类 | 系统聚类也称多层次聚类，分类的单位由高到低呈树形结构，且处位置越低，其包含的对象就越少，但这些对象间的共同特征越多。该聚类方法只适合小数量的时使用，数据量大时速度会非常慢。 |
2.2 K-Means聚类算法
http://blog.csdn.net/qq_36663613/article/details/72784444
K-Means算法是典型的基于距离的非层次聚类算法，在最小化误差函数的基础上将数据划分为预定的类数K，采用距离作为相似性评价指标，即认为两个对象的距离越近，其相似度越大。
（1）算法过程
a:从N个样本数据中随机选取K个对象作为初始的聚类中心；
b:分别计算每个样本到各个聚类中心的距离，将对象分配到距离最近的聚类中；
c:所有对象分类完成后，重新计算K个聚类的中心；
d:与前一次计算得到的K个聚类中心比较，若聚类中心发生变化，转过程2，否则，转过程5；
e:当质心不发生变化时，停止并输出聚类结果。
（2）数据类型与相似性变量
连续属性，先对各属性值进行零——均值规范，再进行距离计算。K-Means算法，一般需先度量样本间（欧几里得距离、曼哈顿距离、闵可夫斯距离） ，样本与簇间（样本到簇中心的距离）及簇与簇间距离（簇中心距离 ）。
文档数据，使用余弦相似性度量，先将文档数据整理成文档——词矩阵格式，再计算相似性
（3）目标函数
使用误差平方和SSE作为度量聚类质量的目标函数，对两种不同的聚类结果，选择误差平方和较小的分类结果。
连续属性的SSE
文档数据的SSE
簇Ei的聚类中心ei
#-*- coding: utf-8 -*-
#使用K-Means算法聚类消费行为特征数据
import pandas as pd
#参数初始化
inputfile = '../data/consumption_data.xls' #销量及其他属性数据
outputfile = '../tmp/data_type.xls' #保存结果的文件名
k = 3 #聚类的类别
iteration = 500 #聚类最大循环次数
data = pd.read_excel(inputfile, index_col = 'Id') #读取数据
data_zs = 1.0*(data - data.mean())/data.std() #数据标准化
from sklearn.cluster import KMeans
model = KMeans(n_clusters = k, n_jobs = 4, max_iter = iteration) #分为k类，并发数4
model.fit(data_zs) #开始聚类
#简单打印结果
r1 = pd.Series(model.labels_).value_counts() #统计各个类别的数目
r2 = pd.DataFrame(model.cluster_centers_) #找出聚类中心
r = pd.concat([r2, r1], axis = 1) #横向连接（0是纵向），得到聚类中心对应的类别下的数目
r.columns = list(data.columns) + [u'类别数目'] #重命名表头
print(r)
#详细输出原始数据及其类别
r = pd.concat([data, pd.Series(model.labels_, index = data.index)], axis = 1) #详细输出每个样本对应的类别
r.columns = list(data.columns) + [u'聚类类别'] #重命名表头
r.to_excel(outputfile) #保存结果
def density_plot(data): #自定义作图函数
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
p = data.plot(kind='kde', linewidth = 2, subplots = True, sharex = False)
[p[i].set_ylabel(u'密度') for i in range(k)]
plt.legend()
return plt
pic_output = '../tmp/pd_' #概率密度图文件名前缀
for i in range(k):
density_plot(data[r[u'聚类类别']==i]).savefig(u'%s%s.png' %(pic_output, i))
2.3 聚类分析算法评价
聚类分析：根据样本数据本身将样本分组。
聚类目标：实现组内对象相互间是相似的结果。
聚类评价：组内相似性越大，组间差别越大，聚类效果越好。
评价方法：
（1）purity评价法【计算正确聚类数占总数的比例】
xk表示第k个聚类的组合，x是聚类的集合，y表示需要被聚类的集合，yi表示第i个对象，n表示被聚类集合对象总数。
（2）RI评价法【排列组合原理对聚类进行评价】
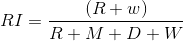
R表示应该被聚在一类的两个对象被正确分类，W表示不应该被聚在一类的两个对象被正确分类，M表示不应该聚在一类的对象被错误归在一类，D表示不应该分开对象被错误分开
（3）F值评价法【RI方法衍生】
2.4 Python主要聚类分析算法
| 对象名 | 函数功能 | 所属工具箱 |
| K-Means | K均值聚类 | sklearn.cluster |
| AffinityPropagation | 吸引力传播聚类（运行效率较低） | sklearn.cluster |
| MeanShift | 均值漂移聚类算法 | sklearn.cluster |
| SpectralClustering | 谱聚类（效果比K均值好，速度比K均值快） | sklearn.cluster |
| AgglomerativeClusering | 层次聚类 | sklearn.cluster |
| DBSCAN | 具有噪声的基于密度的聚类方法 | sklearn.cluster |
| BIRCH | 综合层次聚类算法，适用于大规模数据聚类 | sklearn.cluster |
TSNE：聚类结果可视化工具
#-*- coding: utf-8 -*-
#接k_means.py
from sklearn.manifold import TSNE
tsne = TSNE()
tsne.fit_transform(data_zs) #进行数据降维
tsne = pd.DataFrame(tsne.embedding_, index = data_zs.index) #转换数据格式
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
#不同类别用不同颜色和样式绘图
d = tsne[r[u'聚类类别'] == 0]
plt.plot(d[0], d[1], 'r.')
d = tsne[r[u'聚类类别'] == 1]
plt.plot(d[0], d[1], 'go')
d = tsne[r[u'聚类类别'] == 2]
plt.plot(d[0], d[1], 'b*')
plt.show()
3.关联规则
关联规则目的：在一个数据集中，找出各项之间的关联关系。
3.1 常用关联规则算法
| 算法名称 | 算法描述 |
| Aprior | 关联规则是最常用的挖掘频繁项集的算法，核心是通过连接产生候选项及其支持度然后通过剪枝生成频繁项集 |
| FP-Tree | 针对Aprior算法的固有的多次扫描事务数据集的缺陷，提出不产生候选频繁项集的方法。Aprior和FP-Tree都是寻找频繁项集的算法。 |
| Eclat算法 | Eclat算法是一种深度优先算法，采用垂直数据表示形式，在概念格理论基础上利用基于前缀的等价关系将搜索空间划分为较小的子空间 |
| 灰色关联法 | 分析和确定各因素间影响程度或是若干个子因素（子序列）对主因素（母序列）的贡献度而进行的一种分析方法 |
3.2 Apriori算法
（1）关联规则和频繁项集
A：关联规则的一般形式：
项集A、B同时发生的概率称为关联规则的支持度
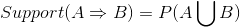
项集A发生，则项集B发生的概率为关联规则的置信度
B:最小支持度和最小置信度
最小支持度：衡量支持度的一个阙值，表示项目集在统计意义上的最低重要性
最小置信度：衡量置信度的一个阙值，表示关联规则的最低可靠性
同时满足最小支持度阙值和最小置信度阙值的规则称为强规则
C：项集
项集是项的集合。包括k个项的项集称为k项集
项集的出现频率是所有包含项集的事务个数
若项集I的相对支持度满足预定义的最小支持度阙值，则I是频繁项集
D：支持度计数
项集A的支持度计数是事务数据集中包含项集A的事务个数，简称为项集的频率或计数
已知项集的支持度计数，则规则A→B的支持度和置信度易从所有事务计数、项集A和项集A U B的支持度计数推出
相关博客：http://blog.csdn.net/wo334499/article/details/51698810
（2）Aprior算法
Aprior算法主要思想是：找出存在于事务数据集中的最大的频繁项集，在利用得到的最大频繁项集与预先设定的最小置信度阙值生成强关联规则
#-*- coding: utf-8 -*-
from __future__ import print_function
import pandas as pd
#自定义连接函数，用于实现L_{k-1}到C_k的连接
def connect_string(x, ms):
x = list(map(lambda i:sorted(i.split(ms)), x))
l = len(x[0])
r = []
for i in range(len(x)):
for j in range(i,len(x)):
if x[i][:l-1] == x[j][:l-1] and x[i][l-1] != x[j][l-1]:
r.append(x[i][:l-1]+sorted([x[j][l-1],x[i][l-1]]))
return r
#寻找关联规则的函数
def find_rule(d, support, confidence, ms = u'--'):
result = pd.DataFrame(index=['support', 'confidence']) #定义输出结果
support_series = 1.0*d.sum()/len(d) #支持度序列
column = list(support_series[support_series > support].index) #初步根据支持度筛选
k = 0
while len(column) > 1:
k = k+1
print(u'\n正在进行第%s次搜索...' %k)
column = connect_string(column, ms)
print(u'数目：%s...' %len(column))
sf = lambda i: d[i].prod(axis=1, numeric_only = True) #新一批支持度的计算函数
#创建连接数据，这一步耗时、耗内存最严重。当数据集较大时，可以考虑并行运算优化。
d_2 = pd.DataFrame(list(map(sf,column)), index = [ms.join(i) for i in column]).T
support_series_2 = 1.0*d_2[[ms.join(i) for i in column]].sum()/len(d) #计算连接后的支持度
column = list(support_series_2[support_series_2 > support].index) #新一轮支持度筛选
support_series = support_series.append(support_series_2)
column2 = []
for i in column: #遍历可能的推理，如{A,B,C}究竟是A+B-->C还是B+C-->A还是C+A-->B？
i = i.split(ms)
for j in range(len(i)):
column2.append(i[:j]+i[j+1:]+i[j:j+1])
cofidence_series = pd.Series(index=[ms.join(i) for i in column2]) #定义置信度序列
for i in column2: #计算置信度序列
cofidence_series[ms.join(i)] = support_series[ms.join(sorted(i))]/support_series[ms.join(i[:len(i)-1])]
for i in cofidence_series[cofidence_series > confidence].index: #置信度筛选
result[i] = 0.0
result[i]['confidence'] = cofidence_series[i]
result[i]['support'] = support_series[ms.join(sorted(i.split(ms)))]
result = result.T.sort(['confidence','support'], ascending = False) #结果整理，输出
print(u'\n结果为：')
print(result)
return result
4.时序模式
4.1 时间序列算法
| 模型名称 | 描述 |
| 平滑法 | 平滑法用于趋势分析和预测，利用修匀技术，削弱短期随机波动对序列的的影响，使序列平滑化。 |
| 趋势拟合法 | 趋势拟合法把时间作为自变量，相变的序列观察值作为因变量，建立回归模型。根据序列特征，可具体分为线性拟合和曲线拟合 |
| 组合模拟 |
时间序列变化主要受长期趋势（T）、季节变动（S）、周期变动（C）和不规则变动（e）影响。根据序列特点，可构建：【加法模型：xt=Tt+St+Ct+εt】【乘法模型：xt=Tt*St*Ct*εt】 |
| AR模型 | |
| MA模型 | |
| ARMA模型 | |
| ARIMA模型 | |
| ARCH模型 | |
| GARCH模型及衍生模型 |
4.2 时间序列预处理
序列预处理：观察值序列的纯随机性和平稳性检验称为序列预处理
纯随机序列（白噪声序列）：序列各项间没有任何相关关系，序列在进行完全无序的随机波动，可终止对该序列的分析。白噪声序列是没有信息可提取的平稳序列。
平稳非白噪声序列：通常是建立一个线性模型来拟合该序列的发展，借此提取该序列额有用信息。常用的模型是：ARMA（平稳序列拟合模型）。
非平稳序列：均值、方差不稳定，处理方法，将其转变为平稳序列，再进行分析。
（1）平稳性检验
a:平稳时间序列定义
单个随机变量X，可计算其均值（数学期望）μ、方差σ2
两个随机变量X、Y，可计算X、Y的协方差cov（X,Y）、相关系数ρ（X,Y）
若时间序列再某一个常数附近波动且波动范围有限，即有常数均值和常数方差。延迟k期的序列变量的自协方差和自相关系数相等，则该时间序列是平稳序列。
b:平稳性检验
时序图检验
自相关图检验
单位根检验
（2）纯随机性检验
若一个序列是纯随机序列，那么它的序列值之间应没有 任何关系，即满足y(k)=0,k!=0，实际上纯随机序列样本自相关系数很接近0，并在0附近随机波动。
纯随机性检验，一般是构造检验统计量来检验序列的纯随机性。常用的检验统计量有Q统计量、LB统计量
由样本各延迟期数的自相关系数可计算得到检验统计量，然后计算出对应的P值，若P值显著大于显著性水平a，则表示该序列不能拒绝纯随机的原假设，可停止对该序列的分析。
4.3 平稳时间序列分析
（1）AR模型
（2）MA模型
（3）ARMA模型
（4）平稳时间序列建模
A：计算ACF和PACF。先计算非平稳白噪声序列的自相关系数（ACF）和偏自相关系数（PACF）
B:ARMA模型识别（模型定阶）。由AR（p）模型、MA（q）、ARMA（p、q）的自相关系数和偏自相关的性质，选择合适的模型
C:估计模型未知参数的值并进行参数检验
D：模型检验
E：模型优化
F：模型应用，短期预测
（5）ARMA模型识别原则
| 模型 | 自相关系数（ACF） | 偏自相关系数（PACF） |
| AR(p) | 拖尾 | p阶截尾 |
| MA(q) | q阶截尾 | 拖尾 |
| ARMA(p,q) | p阶截尾 | q阶拖尾 |
4.4 非平稳时间序列分析
（1）差分运算（具有较强的确定性信息提取能力）
p阶差分：相距一期的两个序列值之间的减法运算称为 1阶差分运算
k步差分：相距k期的两个序列值之间的减法运算称为k步差分运算
（2）ARIMA模型
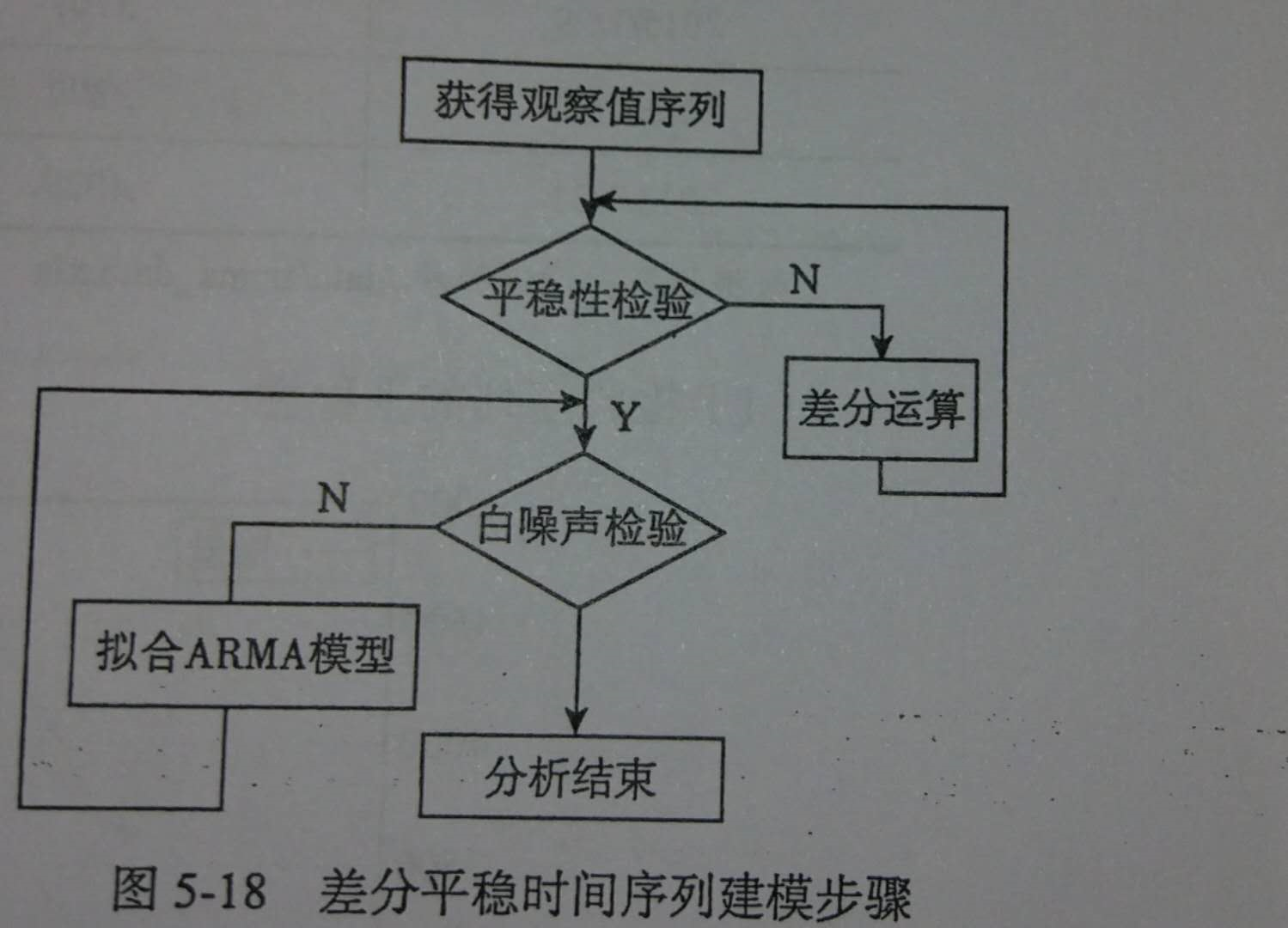
#-*- coding: utf-8 -*-
#arima时序模型实现代码
import pandas as pd
#参数初始化
discfile = '../data/arima_data.xls'
forecastnum = 5
#读取数据，指定日期列为指标，Pandas自动将“日期”列识别为Datetime格式
data = pd.read_excel(discfile, index_col = u'日期')
#时序图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
data.plot()
plt.show()
#自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data).show()
#平稳性检测
from statsmodels.tsa.stattools import adfuller as ADF
print(u'原始序列的ADF检验结果为：', ADF(data[u'销量']))
#返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore
#差分后的结果
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
D_data.plot() #时序图
plt.show()
plot_acf(D_data).show() #自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data).show() #偏自相关图
print(u'差分序列的ADF检验结果为：', ADF(D_data[u'销量差分'])) #平稳性检测
#白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1)) #返回统计量和p值
from statsmodels.tsa.arima_model import ARIMA
data[u'销量'] = data[u'销量'].astype(float)
#定阶
pmax = int(len(D_data)/10) #一般阶数不超过length/10
qmax = int(len(D_data)/10) #一般阶数不超过length/10
bic_matrix = [] #bic矩阵
for p in range(pmax+1):
tmp = []
for q in range(qmax+1):
try: #存在部分报错，所以用try来跳过报错。
tmp.append(ARIMA(data, (p,1,q)).fit().bic)
except:
tmp.append(None)
bic_matrix.append(tmp)
bic_matrix = pd.DataFrame(bic_matrix) #从中可以找出最小值
p,q = bic_matrix.stack().idxmin() #先用stack展平，然后用idxmin找出最小值位置。
print(u'BIC最小的p值和q值为：%s、%s' %(p,q))
model = ARIMA(data, (p,1,q)).fit() #建立ARIMA(0, 1, 1)模型
model.summary2() #给出一份模型报告
model.forecast(5) #作为期5天的预测，返回预测结果、标准误差、置信区间。
4.5 Python主要时序模式算法
| 函数名 | 函数功能 | 所属工具箱 | 使用格式 | 备注 |
| acf() | 计算自相关系数 | statsmodels.tsa.stattools | autocorr=acf(data,unbiased=False,nlags=40,qstat=False,fft=False,alpha=None) | data为观测值序列（时间序列，可以是DataFrame或Series），返回参数autocorr为观测值序列自相关函数，其余的均为可选参数 |
| plot_acf() | 画自相关系数图 | statsmodels.graphics.tsaplots | p=plot_acf(data) | |
| pacf() | 计算偏相关系数 | statsmodels.tsa.stattools | autocorr=pacf(data,unbiased=False,nlags=40,qstat=False,fft=False,alpha=None) | |
| plot_pacf() | 画偏相关系数图 | statsmodels.graphics.tsaplots | p=plot_pacf(data) | |
| adfuller() | 对观测值序列进行单位根检验 | statsmodels.tsa.stattools | h=adffuller(Series,maxlag=None,regression='c',autolag='AIC',store=Fals,regresults=False) | 输入参数Series为一维观测值序列，返回值依次为：adf、pvalue、usedlag、nobs、critical、values、icbest、regresults、resstore |
| diff() | 对观测值序列进行差分计算 | Pandas对象自带的方法 | D.diff() | D为Pandas的DataFrame或Series |
| ARIMA() | 创建一个ARIMA时序模型 | statsmodels.tsa.arima_model | arima=ARIMA(data,(p,1,q)).fit() | data参数为输入的时间序列，p、q为对应的阶，d为差分次数 |
| summary()或summaty2 | 给出一份ARIMA模型的报告 | ARIMA模型对象自带的方法 | arima.summary()/arima.summary2() | arima为已建立好的ARIMA模型，返回一份格式化的模型报告，包含模型的系数、标准误差、p值、AIC、BIC等指标 |
| aic\bic\hqic | 计算ARIMA模型的AIC\BIC\HQIC指标值 | ARIMA模型对象自带的变量 | arima.aic/arima.bic/arima.hqic | arima为已建立好的ARIMA模型，返回值是Model时序模型得到的AIC、BIC、HQIC指标值 |
| forecast() | 应用构建的时序模型进行预测 | ARIMA模型对象自带的方法 | a,b,c=arima.forecast(num) | 输入参数num为要预测的天数，arima为已建立好的ARIMA模型，a为返回的预测值，b为预测的误差，c为预测置信区间 |
| acorr_ljungbox() | Ljung-Box检验，检验是否为白噪声 | statsmodels.tsa.diagnostic | acorr_ljungbox(data,lags=1) | 输入参数data为时间序列数据，lags为滞后数，返回统计量和p值 |
5.离群点检测
离群点成因：数据来源于不同的类、自然变异、数据测量、收集误差
离群点分类：
| 分类标准 | 分类名称 |
| 从数据范围 | 全局离群点和局部离群点 |
| 从数据类型 | 数值型离群点和分类型离群点 |
| 从属性个数 | 一维离群点和多维离群点 |
5.1 离群点检测方法
| 离群点检测方法 | 方法描述 | 方法评估 |
| 基于统计 | 大部分基于统计的离群点检测方法是：构建一个概率分布模型，并计算对象符合该模型的概率，将具有低概率的对象视为离群点 | 前提是：知道数据服从何种分布，对高维数据，检验效果很差 |
| 基于邻近度 | 通常可在数据对象间定义邻近性度量，把远离大部分点的对象视为离群点 |
二维、三维的数据可做散点图观察，大数据不适用，对参数选择敏感，具有全局阙值，不能处理具有不同密度区域的数据集 |
| 基于密度 | 考虑数据集可能存在不同密度区域，离群点是在低密度区域中的对象 | 给出对象是离群点的定量度量，即使数据具有不同的区域很好处理，大数据集不适用，参数选择比较难 |
| 基于聚类 | 一种利用聚类检测离群点的方法是：丢弃远离其他簇的小簇。首先聚类所有对象，然后评估对象属于簇的程度 | 基于聚类技术来发现离群点可能死高度有效的，聚类算法产生的簇的质量对该算法产生的离群点的质量影响非常大 |
5.2 基于模型的离群点检测方法
5.3 基于聚类的离群点检测方法
（1）丢弃远离其他簇的小簇，该过程可简化为丢弃小于某个最小阙值的所有簇。
（2）基于原型的聚类，该过程首先聚类所有对象，然后评估对象属于簇的程度，可用对象到它的簇中心的距离来度量属于簇的程度。
对于基于原型的聚类，有两种方法评估对象属于簇的程度（离群点得分）
a:度量对象到簇原型的距离，并用它作为该对象的离群点得分
b:考虑到簇具有不同的密度，可以度量簇到原型的相对距离，相对距离是点到质心的距离与簇中所有点到质心的距离的中位数之比。
#-*- coding: utf-8 -*-
#使用K-Means算法聚类消费行为特征数据
import numpy as np
import pandas as pd
#参数初始化
inputfile = '../data/consumption_data.xls' #销量及其他属性数据
k = 3 #聚类的类别
threshold = 2 #离散点阈值
iteration = 500 #聚类最大循环次数
data = pd.read_excel(inputfile, index_col = 'Id') #读取数据
data_zs = 1.0*(data - data.mean())/data.std() #数据标准化
from sklearn.cluster import KMeans
model = KMeans(n_clusters = k, n_jobs = 4, max_iter = iteration) #分为k类，并发数4
model.fit(data_zs) #开始聚类
#标准化数据及其类别
r = pd.concat([data_zs, pd.Series(model.labels_, index = data.index)], axis = 1) #每个样本对应的类别
r.columns = list(data.columns) + [u'聚类类别'] #重命名表头
norm = []
for i in range(k): #逐一处理
norm_tmp = r[['R', 'F', 'M']][r[u'聚类类别'] == i]-model.cluster_centers_[i]
norm_tmp = norm_tmp.apply(np.linalg.norm, axis = 1) #求出绝对距离
norm.append(norm_tmp/norm_tmp.median()) #求相对距离并添加
norm = pd.concat(norm) #合并
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
norm[norm <= threshold].plot(style = 'go') #正常点
discrete_points = norm[norm > threshold] #离群点
discrete_points.plot(style = 'ro')
for i in range(len(discrete_points)): #离群点做标记
id = discrete_points.index[i]
n = discrete_points.iloc[i]
plt.annotate('(%s, %0.2f)'%(id, n), xy = (id, n), xytext = (id, n))
plt.xlabel(u'编号')
plt.ylabel(u'相对距离')
plt.show()
